The SABR Model: Explicit Formulae of the Moments of the Forward Prices/Rates Variable and Series Expansions of the Transition Probability Density and of the Option Prices ()
1. Introduction
Let us consider the SABR stochastic volatility model. This model has been introduced in mathematical finance in 2002 by Hagan, Kumar, Lesniewski, Woodward [1] to describe the time dynamics of forward prices/rates and is widely used in the financial markets.
Let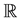 ,
, 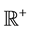 be respectively the sets of real and of positive real numbers and let
be respectively the sets of real and of positive real numbers and let 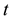 be a real variable that de- notes time. The SABR model describes the dynamics of two variables: the forward prices/rates variable
be a real variable that de- notes time. The SABR model describes the dynamics of two variables: the forward prices/rates variable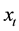 ,
,  , and the stochastic volatility variable
, and the stochastic volatility variable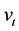 ,
,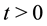 . The variables
. The variables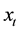 ,
,  ,
, 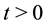 , are real stochastic pro- cesses that satisfy the following system of stochastic differential equations:
, are real stochastic pro- cesses that satisfy the following system of stochastic differential equations:
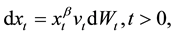 (1)
(1)
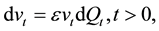 (2)
(2)
where 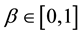 and
and  are real parameters. The parameters
are real parameters. The parameters 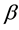 and
and 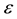 of (1), (2) are called respectively
of (1), (2) are called respectively ![]() -volatility and volatility of volatility. The choices
-volatility and volatility of volatility. The choices ![]() and
and ![]() define respectively the normal and the lognormal SABR models and are not considered here. The normal and lognormal SABR models have been widely studied in the scientific literature (see, for example, [1]-[9]). In this paper we restrict our attention to the study of the case
define respectively the normal and the lognormal SABR models and are not considered here. The normal and lognormal SABR models have been widely studied in the scientific literature (see, for example, [1]-[9]). In this paper we restrict our attention to the study of the case![]() . The stochastic processes
. The stochastic processes![]() ,
, ![]() ,
, ![]() , are standard Wiener processes such that
, are standard Wiener processes such that ![]()
![]() ,
, ![]() ,
, ![]() , are their stochastic differentials and we assume that:
, are their stochastic differentials and we assume that:
![]() (3)
(3)
where ![]() denotes the expected value of
denotes the expected value of ![]() and
and ![]() is a constant called correlation coefficient. The Equations (1), (2) are equipped with the initial conditions:
is a constant called correlation coefficient. The Equations (1), (2) are equipped with the initial conditions:
![]() (4)
(4)
![]() (5)
(5)
where ![]() and
and ![]() are random variables that we assume to be concentrated in a point with probability one. For simplicity we identify these random variables with the points where they are concentrated. Moreover we assume
are random variables that we assume to be concentrated in a point with probability one. For simplicity we identify these random variables with the points where they are concentrated. Moreover we assume![]() . The assumption
. The assumption ![]() with probability one and Equation (2) imply that
with probability one and Equation (2) imply that ![]() with probability one for
with probability one for![]() . It is known that when
. It is known that when ![]() the stochastic volatility model (1), (2) with the conditions (3), (4), (5) is underspecified (see [9] [10] [11]). In fact when
the stochastic volatility model (1), (2) with the conditions (3), (4), (5) is underspecified (see [9] [10] [11]). In fact when ![]() the origin of the forward prices/rates variable
the origin of the forward prices/rates variable![]() ,
, ![]() , is “accessible” from
, is “accessible” from![]() , and in the origin of the forward prices/rates variable equation (1) has not a unique solution. In order to guarantee the uniqueness of the solution of (1), (2), (3), (4), (5) and the no arbitrage condition we impose an absorbing barrier in zero to the forward prices/rates stochastic process
, and in the origin of the forward prices/rates variable equation (1) has not a unique solution. In order to guarantee the uniqueness of the solution of (1), (2), (3), (4), (5) and the no arbitrage condition we impose an absorbing barrier in zero to the forward prices/rates stochastic process![]() ,
, ![]() , (see [10] [11] for details). This means that the paths of the stochastic process
, (see [10] [11] for details). This means that the paths of the stochastic process![]() ,
, ![]() , that reach zero are no longer considered in the time evolution. The absorbing barrier in zero imposed to the forward prices/rates variable is only one of the conditions discussed in the scientific literature that can be used to guarantee uniqueness of the solution of the initial value problem (1), (2), (3), (4), (5). For example reflecting barriers and mixed barriers in zero have been suggested as conditions that guarantee uniqueness. We study the model with the absorbing barrier just for simplicity. The results obtained here for this model can be extended to several mo- dels with other uniqueness conditions. The absorbing barrier in zero imposed to the forward prices/rates process implies that the time evolution defined by the model equations (1), (2) does not conserve probability. Despite this fact we continue to call probability density function the fundamental solution of the backward Kolmokorov equation associated to (1), (2) that satisfies the homogeneous Dirichlet boundary condition when the forward prices/rates variable is zero. This boundary condition imposed to the probability density function corresponds to the absorbing barrier in zero imposed to the forward prices/rates variable. The SABR model studied in this paper is defined by the equations (1), (2), (3), (4), (5), by the conditions
, that reach zero are no longer considered in the time evolution. The absorbing barrier in zero imposed to the forward prices/rates variable is only one of the conditions discussed in the scientific literature that can be used to guarantee uniqueness of the solution of the initial value problem (1), (2), (3), (4), (5). For example reflecting barriers and mixed barriers in zero have been suggested as conditions that guarantee uniqueness. We study the model with the absorbing barrier just for simplicity. The results obtained here for this model can be extended to several mo- dels with other uniqueness conditions. The absorbing barrier in zero imposed to the forward prices/rates process implies that the time evolution defined by the model equations (1), (2) does not conserve probability. Despite this fact we continue to call probability density function the fundamental solution of the backward Kolmokorov equation associated to (1), (2) that satisfies the homogeneous Dirichlet boundary condition when the forward prices/rates variable is zero. This boundary condition imposed to the probability density function corresponds to the absorbing barrier in zero imposed to the forward prices/rates variable. The SABR model studied in this paper is defined by the equations (1), (2), (3), (4), (5), by the conditions![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and by the absorbing barrier in zero imposed to the forward prices/rates variable.
, and by the absorbing barrier in zero imposed to the forward prices/rates variable.
The practice of the financial markets has shown that in many circumstances this SABR model fits satisfac- torily the implied volatility curves associated to the observed option prices and is able to capture the dynamics of the implied volatility smile. Moreover it yields stable hedges of elementary portfolios built with the asset un- derlying the forward prices/rates variable and its derivative products (see, for example, [1] [12]). These facts jus- tify the use of the SABR model by the practitioners and the interest in the SABR model of the research com- munity. Some approximate expressions of the probability density function of the SABR model, of the corres- ponding European option prices and of the implied volatility associated to the option prices are available in the scientific literature. These formulae have been obtained using several mathematical methods, such as singular perturbation theory and heat kernel asymptotics (see [1] [13] [14]). For example an explicit formula (involving a one dimensional integral) for the transition probability density function of the SABR model when ![]() or
or ![]() and
and ![]() has been obtained in [4]. Similar results are contained in [15] when
has been obtained in [4]. Similar results are contained in [15] when![]() ,
, ![]() and in [7] for a modified SABR model. In [16] an option pricing problem is studied. Let
and in [7] for a modified SABR model. In [16] an option pricing problem is studied. Let ![]() be the current time,
be the current time, ![]() be the maturity time of the options considered and
be the maturity time of the options considered and ![]() be the total volatility of volatility. The SABR model for
be the total volatility of volatility. The SABR model for ![]() is studied and it is derived a series expansion in powers of the total volatility of volatility of the transition probability density function of the variables
is studied and it is derived a series expansion in powers of the total volatility of volatility of the transition probability density function of the variables![]() ,
, ![]() ,
, ![]() , of the SABR model (1), (2), (3), (4), (5),
, of the SABR model (1), (2), (3), (4), (5), ![]() ,
, ![]() , when no condition in zero is imposed to the forward prices/rates variable [16]. The terms of the expansion in powers of
, when no condition in zero is imposed to the forward prices/rates variable [16]. The terms of the expansion in powers of ![]() are obtained scaling the variables of the model and using a trans- formation of the bivariate normal function. Explicit formulae are given for the first three terms of the expansion in powers of
are obtained scaling the variables of the model and using a trans- formation of the bivariate normal function. Explicit formulae are given for the first three terms of the expansion in powers of ![]() of the probability density function and of the corresponding expansions of the European option prices. The idea of imposing an absorbing barrier in zero to the forward prices/rates variable of the SABR model is discussed in [3]. In particular in [3] in order to price long dated options in the SABR model it is sug- gested the idea of completing the probability density function determined imposing the absorbing barrier in zero to the forward prices/rates variable adding a term proportional to a Dirac’s delta supported on the absorbing bar- rier. The choice of the Dirac's delta term restores the probability conservation during the time evolution.
of the probability density function and of the corresponding expansions of the European option prices. The idea of imposing an absorbing barrier in zero to the forward prices/rates variable of the SABR model is discussed in [3]. In particular in [3] in order to price long dated options in the SABR model it is sug- gested the idea of completing the probability density function determined imposing the absorbing barrier in zero to the forward prices/rates variable adding a term proportional to a Dirac’s delta supported on the absorbing bar- rier. The choice of the Dirac's delta term restores the probability conservation during the time evolution.
In this paper for the previously specified SABR model we deduce a series expansion in powers of the cor- relation coefficient ![]() of the transition probability density function. Explicit expressions of the first three terms of this expansion are derived. These terms are integrals of known integrands. In particular the zero-th order term of the expansion is a one dimensional integral whose integrand is expressed using only elementary functions. This is a new formula of the probability density function of the SABR model when
of the transition probability density function. Explicit expressions of the first three terms of this expansion are derived. These terms are integrals of known integrands. In particular the zero-th order term of the expansion is a one dimensional integral whose integrand is expressed using only elementary functions. This is a new formula of the probability density function of the SABR model when![]() . Previously this pro- bability density function was known only through a formula consisting in a one dimensional integral of an ex- pression involving non elementary transcendental functions [9]. Related formulae have been derived by several authors. For example in [17] a formula for the marginal distribution of the forward prices/rates variable of the SABR model when
. Previously this pro- bability density function was known only through a formula consisting in a one dimensional integral of an ex- pression involving non elementary transcendental functions [9]. Related formulae have been derived by several authors. For example in [17] a formula for the marginal distribution of the forward prices/rates variable of the SABR model when ![]() is presented. The terms of the expansion of the probability density function present- ed in this paper are integrals of the product of a function depending on the forward prices/rates variable and the integration variable times a function depending on the stochastic volatility variable and the integration variable (see, for example, formula (34)). The integration variable, in general, is a vector valued variable and the corres- ponding integral is a multidimensional integral. Furthermore we show that for
is presented. The terms of the expansion of the probability density function present- ed in this paper are integrals of the product of a function depending on the forward prices/rates variable and the integration variable times a function depending on the stochastic volatility variable and the integration variable (see, for example, formula (34)). The integration variable, in general, is a vector valued variable and the corres- ponding integral is a multidimensional integral. Furthermore we show that for ![]() the
the ![]() -th order term of the expansion in powers of
-th order term of the expansion in powers of ![]() of the probability density function of the SABR model can be written as the con- volution of the zero-th order term with a “forcing” function.
of the probability density function of the SABR model can be written as the con- volution of the zero-th order term with a “forcing” function.
The terms of the expansion in powers of ![]() of the probability density function of the SABR model are the solutions order by order in perturbation theory of the final value problem for the backward Kolmogorov equa- tion satisfied by the probability density function of the model. The partial differential operator that appears in the final value problems satisfied by the terms of the expansion can be “diagonalized” using a procedure based on a change of variables, and on the Hankel and the Kontorovich-Lebedev transforms [18] [19]. This “diago- nalization” procedure makes possible to obtain integral formulae for the expansion terms. In particular the “di- agonalization” procedure shows that the zero-th order term of the expansion is a kind of convolution between two kernels, one depending from the transformed forward prices/rates variable and the other depending from the stochastic volatility variable. This last kernel has already been used in [4] to express the transition probability density function of the SABR model when
of the probability density function of the SABR model are the solutions order by order in perturbation theory of the final value problem for the backward Kolmogorov equa- tion satisfied by the probability density function of the model. The partial differential operator that appears in the final value problems satisfied by the terms of the expansion can be “diagonalized” using a procedure based on a change of variables, and on the Hankel and the Kontorovich-Lebedev transforms [18] [19]. This “diago- nalization” procedure makes possible to obtain integral formulae for the expansion terms. In particular the “di- agonalization” procedure shows that the zero-th order term of the expansion is a kind of convolution between two kernels, one depending from the transformed forward prices/rates variable and the other depending from the stochastic volatility variable. This last kernel has already been used in [4] to express the transition probability density function of the SABR model when ![]() or
or ![]() and
and![]() , and in [9] [15] to study respec- tively a modified SABR model when
, and in [9] [15] to study respec- tively a modified SABR model when![]() ,
, ![]() and when
and when ![]() and
and![]() . Previously the same kernel has been used in the study of the transition probability density function of the time integral of a geometric Brownian motion (see [15] [20]).
. Previously the same kernel has been used in the study of the transition probability density function of the time integral of a geometric Brownian motion (see [15] [20]).
Despite the fact that the SABR model with ![]() and the absorbing barrier mentioned above does not conserve probability it is common practice to use the “risk neutral approach” to price options in the SABR mo- del framework as “expected values” of the discounted payoff functions. We follow this practice and we extend the method used to derive the expansion in powers of
and the absorbing barrier mentioned above does not conserve probability it is common practice to use the “risk neutral approach” to price options in the SABR mo- del framework as “expected values” of the discounted payoff functions. We follow this practice and we extend the method used to derive the expansion in powers of ![]() of the transition probability density function to de- duce the corresponding expansions of the European call and put option prices in the SABR model. The terms of these expansions are integrals of known integrands. The integrands are expressed as the product of a function depending from the forward prices/rates variable and the integration variable times a function depending from the stochastic volatility variable and the integration variable. Some of these integrals are done analytically, this guarantees that (order by order in perturbation theory) the option prices can be obtained evaluating numerically integrals of the same dimension than those that must be evaluated to obtain the transition probability density function. Moreover these integrals due to the special structure of their integrands can be computed using ad hoc quadrature rules. The development of these ad hoc quadrature rules is beyond our purposes in this paper. Finally we study the moments of the forward prices/rates variable. For these moments we obtain closed form formulae that do not contain integrals or series expansions. These formulae are polynomials in the correlation coefficient
of the transition probability density function to de- duce the corresponding expansions of the European call and put option prices in the SABR model. The terms of these expansions are integrals of known integrands. The integrands are expressed as the product of a function depending from the forward prices/rates variable and the integration variable times a function depending from the stochastic volatility variable and the integration variable. Some of these integrals are done analytically, this guarantees that (order by order in perturbation theory) the option prices can be obtained evaluating numerically integrals of the same dimension than those that must be evaluated to obtain the transition probability density function. Moreover these integrals due to the special structure of their integrands can be computed using ad hoc quadrature rules. The development of these ad hoc quadrature rules is beyond our purposes in this paper. Finally we study the moments of the forward prices/rates variable. For these moments we obtain closed form formulae that do not contain integrals or series expansions. These formulae are polynomials in the correlation coefficient![]() . The coefficients of these polynomials are closed form expressions containing only elementary functions of the remaining quantities defining the model. In [5] and [6] similar moment formulae have been obtained for the normal (i.e.
. The coefficients of these polynomials are closed form expressions containing only elementary functions of the remaining quantities defining the model. In [5] and [6] similar moment formulae have been obtained for the normal (i.e.![]() ) and for the lognormal (i.e.
) and for the lognormal (i.e.![]() ) SABR models.
) SABR models.
Some numerical experiments on synthetic and on real data are discussed. In particular using the option pricing formulae mentioned above we study the daily values of the futures price of the EUR/USD currency’s exchange rate having maturity September 16th, 2011 and of the daily prices of the corresponding European call and put options with expiry date September 9th, 2011 and strike prices![]() ,
,![]() . The prices
. The prices![]() ,
, ![]() , are expressed in USD. More specifically we study the daily closing prices of these contracts observed at the New York Stock Exchange in the time period going from September 27th, 2010, to July 19th, 2011.
, are expressed in USD. More specifically we study the daily closing prices of these contracts observed at the New York Stock Exchange in the time period going from September 27th, 2010, to July 19th, 2011.
The numerical experiments discussed show two facts. The first one is that when the SABR model with the absorbing barrier in zero is considered the numerical evaluation with the Monte Carlo method of option prices can be computationally expansive. In fact in the SABR model the loss of probability during the time evolution is a function of ![]() and
and ![]() and increases when
and increases when ![]() increases and/or
increases and/or ![]() decreases. As a consequence when
decreases. As a consequence when ![]() increases and/or
increases and/or ![]() decreases the size of the Monte Carlo sample used to evaluate option prices with a given accuracy must increase to compensate the probability loss during the time evolution. For example in Section 5 it is shown that when
decreases the size of the Monte Carlo sample used to evaluate option prices with a given accuracy must increase to compensate the probability loss during the time evolution. For example in Section 5 it is shown that when![]() ,
, ![]() in a test case for an option with time to maturity
in a test case for an option with time to maturity ![]() to get three correct significant digits in the numerical approximation of its price it is necessary to consider a Monte Carlo sample of 1600000 points. This sample is generated computing 1,600,000 trajectories of (1), (2). This must be compared with the fact that the accuracy of the option prices obtained using the series expansions in powers of
to get three correct significant digits in the numerical approximation of its price it is necessary to consider a Monte Carlo sample of 1600000 points. This sample is generated computing 1,600,000 trajectories of (1), (2). This must be compared with the fact that the accuracy of the option prices obtained using the series expansions in powers of ![]() derived in this paper depends from
derived in this paper depends from ![]() and from the quadrature rule used in the numerical evaluation of the integrals contained in the coefficients of the series expansions, but is substantially independent of
and from the quadrature rule used in the numerical evaluation of the integrals contained in the coefficients of the series expansions, but is substantially independent of![]() . A test case shows that the time required to evaluate one option price with three correct significant digits on a Centrino Intel Core Duo CPU T6400 processor is a few tens of seconds using the series expansions derived here. The evaluation with the Monte Carlo method of the same price with the same accuracy requires about 500 seconds and the use of a sample generated computing 400000 trajectories of (1), (2). The second fact is that the SABR model interprets satisfactorily the time series of real data studied, that is the time series of futures prices of the EUR/USD currency’s exchange rate and of the corresponding option prices. In fact in the time period considered that goes from September 27th, 2010, to July 19th, 2011 the calibration the SABR model using as data the clo- sing values of a day of a set of option prices on the futures prices of the EUR/USD currency’s exchange rate ob- served at the New York Stock Exchange shows that a unique set of parameter values explains the entire data set considered. Moreover the parameter values resulting from the calibration and the option pricing formulae are used to forecast option prices. The comparison between forecast option prices and option prices actually obser- ved in the market confirms the validity of the model and of the calibration procedure used.
. A test case shows that the time required to evaluate one option price with three correct significant digits on a Centrino Intel Core Duo CPU T6400 processor is a few tens of seconds using the series expansions derived here. The evaluation with the Monte Carlo method of the same price with the same accuracy requires about 500 seconds and the use of a sample generated computing 400000 trajectories of (1), (2). The second fact is that the SABR model interprets satisfactorily the time series of real data studied, that is the time series of futures prices of the EUR/USD currency’s exchange rate and of the corresponding option prices. In fact in the time period considered that goes from September 27th, 2010, to July 19th, 2011 the calibration the SABR model using as data the clo- sing values of a day of a set of option prices on the futures prices of the EUR/USD currency’s exchange rate ob- served at the New York Stock Exchange shows that a unique set of parameter values explains the entire data set considered. Moreover the parameter values resulting from the calibration and the option pricing formulae are used to forecast option prices. The comparison between forecast option prices and option prices actually obser- ved in the market confirms the validity of the model and of the calibration procedure used.
The website: http://www.econ.univpm.it/recchioni/finance/w18 contains some auxiliary material including animations, an interactive application and an app that helps the understanding of this paper. A more general reference to the work of the authors and of their coauthors in mathematical finance is the website: http://www.econ.univpm.it/recchioni/finance.
The remainder of the paper is organized as follows. In Section 2 we derive the expansion in powers of ![]() of the transition probability density function associated to the SABR model (1), (2), (3), (4), (5) with the previously specified absorbing barrier. In Section 3, using “the risk neutral approach”, we derive the corresponding ex- pansions in powers of
of the transition probability density function associated to the SABR model (1), (2), (3), (4), (5) with the previously specified absorbing barrier. In Section 3, using “the risk neutral approach”, we derive the corresponding ex- pansions in powers of ![]() of the European call and put option prices. In Section 4 we derive closed form for- mulae for the moments of the forward prices/rates variable
of the European call and put option prices. In Section 4 we derive closed form for- mulae for the moments of the forward prices/rates variable![]() ,
,![]() . Finally in Section 5 we use the series ex- pansions of the option prices derived in Section 3 to study numerically time series of synthetic and real data.
. Finally in Section 5 we use the series ex- pansions of the option prices derived in Section 3 to study numerically time series of synthetic and real data.
2. The Series Expansion of the probability density Function
Let us study the transition probability density function of the stochastic processes![]() ,
, ![]() ,
, ![]() , implicitly de- fined by (1), (2), (3), (4), (5) and by the absorbing barrier in zero imposed to
, implicitly de- fined by (1), (2), (3), (4), (5) and by the absorbing barrier in zero imposed to![]() ,
,![]() .
.
2.1. The Initial Value problems Satisfied by the Expansion terms
Let us define the stochastic process:
![]() (6)
(6)
From Equations (1), (2) and Ito's lemma it follows that![]() ,
, ![]() ,
, ![]() , satisfy the following system of sto- chastic differential equations:
, satisfy the following system of sto- chastic differential equations:
![]() (7)
(7)
![]() (8)
(8)
The initial conditions (4), (5) become:
![]() (9)
(9)
![]() (10)
(10)
An absorbing barrier in zero is imposed to the stochastic process![]() ,
,![]() . The barrier imposed to
. The barrier imposed to![]() ,
, ![]() , follows from the analogous barrier imposed to
, follows from the analogous barrier imposed to![]() ,
,![]() .
.
Let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , be the transition probability density function of model (1), (2), (3), (4), (5) with the previously specified absorbing barrier imposed to
, be the transition probability density function of model (1), (2), (3), (4), (5) with the previously specified absorbing barrier imposed to![]() ,
, ![]() , that is let
, that is let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , be the probability density function of having
, be the probability density function of having![]() ,
, ![]() given the fact that we have
given the fact that we have![]() ,
, ![]() when
when![]() . Let
. Let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , be the transition probability density function of model (7), (8), (3), (9), (10) with the absorbing barrier previously specified imposed to
, be the transition probability density function of model (7), (8), (3), (9), (10) with the absorbing barrier previously specified imposed to![]() ,
, ![]() , that is let
, that is let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , be the probability density function of having
, be the probability density function of having![]() ,
, ![]() given the fact that we have
given the fact that we have![]() ,
, ![]() when
when![]() . We have:
. We have:
![]() (11)
(11)
Formula (11) shows that the series expansion in powers of ![]() of
of ![]() can be easily deduced from the series expansion in powers of
can be easily deduced from the series expansion in powers of ![]() of
of![]() .
.
Let us deduce the series expansion in powers of ![]() of
of![]() . The function
. The function ![]() is the solution of the backward Kolmogorov equation associated to (7), (8), that is:
is the solution of the backward Kolmogorov equation associated to (7), (8), that is:
![]() (12)
(12)
with final condition:
![]() (13)
(13)
and boundary condition:
![]() (14)
(14)
where ![]() is the Dirac's delta. The Dirichlet boundary condition (14) imposes to the function
is the Dirac's delta. The Dirichlet boundary condition (14) imposes to the function ![]() the condition that corresponds to the absorbing barrier in zero imposed to the stochastic process
the condition that corresponds to the absorbing barrier in zero imposed to the stochastic process![]() ,
,![]() . Note that
. Note that ![]() does not depend from
does not depend from ![]() and
and ![]() separately, it depends only from
separately, it depends only from![]() . Let us introduce the function
. Let us introduce the function![]() , where
, where![]() ,
, ![]() ,
,![]() . From (12), (13), (14) it follows that
. From (12), (13), (14) it follows that ![]() is the solution of the partial differential equation:
is the solution of the partial differential equation:
![]() (15)
(15)
with initial condition:
![]() (16)
(16)
and boundary condition:
![]() (17)
(17)
Let us assume that:
![]() (18)
(18)
where the functions![]() ,
, ![]() , do not depend from
, do not depend from![]() . Substituting the series (18) in (15), (16), (17), dif- ferentiating (18) term by term and equating the coefficients of the terms of the same degree in
. Substituting the series (18) in (15), (16), (17), dif- ferentiating (18) term by term and equating the coefficients of the terms of the same degree in ![]() we obtain the following problems:
we obtain the following problems:
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
and
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
Moreover from (19), (20), (21) and (22), (23), (24) we have:
![]() (25)
(25)
Formula (25) is one of the formulae announced in the Introduction. In fact for ![]() formula (25) gives
formula (25) gives ![]() as the convolution of the zero-th order term of the expansion
as the convolution of the zero-th order term of the expansion ![]() with the “forcing” function
with the “forcing” function![]() .
.
2.2. The Zero-th Order term of the Expansion
Let ![]() be the set of complex numbers,
be the set of complex numbers, ![]() be the imaginary unit and let
be the imaginary unit and let![]() ,
,![]() . Note that when
. Note that when ![]() we have
we have![]() . The formulae that follow, unless diversely specified, hold for
. The formulae that follow, unless diversely specified, hold for![]() ,
,![]() .
.
Let us study problem (19), (20), (21). The function ![]() solution of (19), (20), (21) can be written as follows:
solution of (19), (20), (21) can be written as follows:
![]() (26)
(26)
where ![]() is the first kind Bessel function of index
is the first kind Bessel function of index ![]() (see [21] pag. 358) and
(see [21] pag. 358) and ![]() is a function to be de- termined. It is easy to see that when the integral contained in (26) and its integrand are “well behaved” the function
is a function to be de- termined. It is easy to see that when the integral contained in (26) and its integrand are “well behaved” the function ![]() given by (26) satisfies the boundary condition (21). In fact when
given by (26) satisfies the boundary condition (21). In fact when ![]() we have
we have![]() ,
,![]() . In order to determine the function
. In order to determine the function ![]() of (26) let us impose equation (19) under the integral sign in (26). We have:
of (26) let us impose equation (19) under the integral sign in (26). We have:
![]() (27)
(27)
Using [21] page 362 formula 9.1.52equation (27) becomes:
![]() (28)
(28)
and from (26) we have:
![]() (29)
(29)
From [21] page 374 formula 9.6.1 and (29) it follows that ![]() can be written as a Laplace transform, that is we have:
can be written as a Laplace transform, that is we have:
![]() (30)
(30)
where ![]() is the imaginary unit,
is the imaginary unit, ![]() is the second kind modified Bessel function of index
is the second kind modified Bessel function of index![]() , also known as Macdonald function (see [21] pag. 374), and
, also known as Macdonald function (see [21] pag. 374), and ![]() is a function to be determined. From (26) and (30) we have:
is a function to be determined. From (26) and (30) we have:
![]() (31)
(31)
To determine the function![]() ,
, ![]() ,
, ![]() , we impose to
, we impose to ![]() the initial condition (20). To do this we recall the following formulae (see [22] Section 11.2):
the initial condition (20). To do this we recall the following formulae (see [22] Section 11.2):
![]() (32)
(32)
and (see [4] [23])
![]() (33)
(33)
where ![]() is the real part of the complex number
is the real part of the complex number ![]() and
and ![]() denotes the hyperbolic sine function. From (16), (31), (32), (33) we have:
denotes the hyperbolic sine function. From (16), (31), (32), (33) we have:
![]() (34)
(34)
where ![]() and
and ![]() are given by:
are given by:
![]() (35)
(35)
![]() (36)
(36)
where ![]() denotes the hyperbolic cosine function and
denotes the hyperbolic cosine function and ![]() is given by:
is given by:
![]() (37)
(37)
From [24] page 146 formula 25 we have:
![]() (38)
(38)
Computing explicitly the integrals in the ![]() and
and ![]() variables contained respectively in formulae (34) and (36) we have:
variables contained respectively in formulae (34) and (36) we have:
![]() (39)
(39)
where
![]() (40)
(40)
and
![]() (41)
(41)
It is easy to see that the function ![]() is positive for
is positive for![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Moreover the function ![]() defined in (??) satisfies the boundary condition (21). In fact when
defined in (??) satisfies the boundary condition (21). In fact when ![]() the term
the term ![]() is zero and the functions
is zero and the functions ![]() and
and ![]() are bounded in
are bounded in![]() ,
, ![]() for
for![]() ,
, ![]() ,
, ![]() (i.e. the functions
(i.e. the functions ![]() and
and ![]() are “well behaved”).
are “well behaved”).
Formula (39) of ![]() expresses the probability density function of the SABR model when
expresses the probability density function of the SABR model when ![]() using only elementary functions. This last fact makes the numerical evaluation of (39) easy and efficient. Previously only a formula of
using only elementary functions. This last fact makes the numerical evaluation of (39) easy and efficient. Previously only a formula of ![]() as a one dimensional integral of an integrand involving non elementary transcendental functions was known [9]. Note that using (11) from formula (39) that gives
as a one dimensional integral of an integrand involving non elementary transcendental functions was known [9]. Note that using (11) from formula (39) that gives ![]() expressed in the variables
expressed in the variables![]() ,
, ![]() ,
, ![]() , it is easy to deduce the corresponding formula of the probability density function of the SABR model when
, it is easy to deduce the corresponding formula of the probability density function of the SABR model when ![]() expressed in the variables
expressed in the variables![]() ,
, ![]() ,
,![]() . That is formula (39) and the analogous formula in the variables
. That is formula (39) and the analogous formula in the variables![]() ,
, ![]() ,
, ![]() , are the formulae that have been announced in the Introduction for the probability density function when
, are the formulae that have been announced in the Introduction for the probability density function when![]() .
.
For later convenience the function ![]() defined in (38) is rewritten as follows:
defined in (38) is rewritten as follows:
![]() (42)
(42)
where ![]() is given by (37) and
is given by (37) and
![]() (43)
(43)
Moreover let us define![]() ,
, ![]() ,
,![]() . Using the identities satisfied by the Mcdonald
. Using the identities satisfied by the Mcdonald
functions (see [21] pag. 376, formula 9.6.28) we have:
![]() (44)
(44)
where
![]() (45)
(45)
Formulae (44), (45) will be used later.
2.3. Thefirst and Second order Terms of the Expansion
Let us consider the functions![]() ,
, ![]() defined in (18). Proceeding as in Section 2.2 it can be shown that chang- ing the integration order in (25) when
defined in (18). Proceeding as in Section 2.2 it can be shown that chang- ing the integration order in (25) when ![]() we have:
we have:
![]() (46)
(46)
where the functions ![]() and
and ![]() are given by:
are given by:
![]() (47)
(47)
and
![]() (48)
(48)
Similarly changing the integration order in (25) when ![]() we have:
we have:
![]() (49)
(49)
where the functions ![]() and
and ![]() are given by:
are given by:
![]() (50)
(50)
and
![]() (51)
(51)
Using (35) and the properties of the functions ![]() (see [21] p. 361 formula 9.1.27) we have:
(see [21] p. 361 formula 9.1.27) we have:
![]() (52)
(52)
and
![]() (53)
(53)
where
![]() (54)
(54)
Using (43), (44) we can rewrite the functions![]() ,
, ![]() , defined in (48), (51), as follows:
, defined in (48), (51), as follows:
![]() (55)
(55)
and
![]() (56)
(56)
The formulae (46), (49) for![]() ,
, ![]() are new. Similar formulae can be deduced for the higher order terms of the expansion, that is for the functions
are new. Similar formulae can be deduced for the higher order terms of the expansion, that is for the functions![]() ,
,![]() . These formulae become more and more involved when
. These formulae become more and more involved when ![]() increases.
increases.
Note that given ![]() to approximate the integrals (55), (56) using a quadrature rule it is sufficient to
to approximate the integrals (55), (56) using a quadrature rule it is sufficient to
evaluate the functions ![]() and
and ![]() on a grid of the set
on a grid of the set
![]() . This means that exploiting the “structure” of the
. This means that exploiting the “structure” of the
integrands of (55), (56) ad hoc quadrature rules can be built to evaluate efficiently the integrals (55), (56). We do not consider the problem of building these quadrature rules here.
3. The Series Expansion of the option prices
To price European call and put options in the SABR model we use the no arbitrage pricing theory. Let us as- sume that the risk free interest rate is constant in time. This hypothesis guarantees that the forward prices/rates variable![]() ,
, ![]() , is a martingale under the risk-neutral measure (see [25] Proposition 3.1). That is in this case the risk neutral measure used to compute the option prices coincides with the “physical” measure used to de- scribe the dynamics of
, is a martingale under the risk-neutral measure (see [25] Proposition 3.1). That is in this case the risk neutral measure used to compute the option prices coincides with the “physical” measure used to de- scribe the dynamics of![]() ,
, ![]() ,
, ![]() , defined implicitly by (1), (2), (3), (4), (5) with the absorbing barrier in zero imposed to the variable
, defined implicitly by (1), (2), (3), (4), (5) with the absorbing barrier in zero imposed to the variable![]() ,
,![]() .
.
Let ![]() and
and ![]() be respectively the prices at time
be respectively the prices at time ![]() of a European call and put option having maturity time
of a European call and put option having maturity time ![]() and strike price
and strike price![]() . Under the assumption of constant risk free interest rate the no arbitrage theory implies that:
. Under the assumption of constant risk free interest rate the no arbitrage theory implies that:
![]() (57)
(57)
![]() (58)
(58)
where ![]() and
and ![]() is the risk free interest rate.
is the risk free interest rate.
Using the change of variable (6) and formula (11) the prices ![]() and
and ![]() defined by (57) and (58) can be rewritten as follows:
defined by (57) and (58) can be rewritten as follows:
![]() (59)
(59)
![]() (60)
(60)
where![]() .
.
In analogy with the analysis of Section 2.1, let us deduce the first three terms of the expansion in powers of ![]() of
of ![]() and
and![]() . We begin considering the expansion in powers of
. We begin considering the expansion in powers of ![]() of
of![]() . Substituting (18) into Equation (60) and integrating term by term the resulting series we obtain the following formula:
. Substituting (18) into Equation (60) and integrating term by term the resulting series we obtain the following formula:
![]() (61)
(61)
where
![]() (62)
(62)
Let us recall the following formulae (see [21] pag. 484, formulae 11.3.20, 11.3.21, pag. 486 formula 11.4.17):
![]() (63)
(63)
![]() (64)
(64)
Substituting (34), (35) in (62) and using formulae (63), (64) when ![]() we have:
we have:
![]() (65)
(65)
where![]() , and the functions
, and the functions ![]() and
and ![]() are given by:
are given by:
![]() (66)
(66)
and
![]() (67)
(67)
Substituting (46), (52) in (62) when ![]() we have:
we have:
![]()
![]() (68)
(68)
where ![]() is given by:
is given by:
![]() (69)
(69)
Finally substituting (46), (53) in (62) when ![]() we have:
we have:
![]() (70)
(70)
where ![]() is given by:
is given by:
![]() (71)
(71)
Let us deduce the expansion in powers of ![]() of the European call option price
of the European call option price ![]() corresponding to the expansion (61) of the European put option price
corresponding to the expansion (61) of the European put option price![]() . Substituting (18) in (59) and integrating term by term the resulting series we obtain the following formula:
. Substituting (18) in (59) and integrating term by term the resulting series we obtain the following formula:
![]() (72)
(72)
where
![]() (73)
(73)
It is easy to see that:
![]() (74)
(74)
Relation (74) is the analogous in the SABR model context of the well known put-call parity relation of mathematical finance. Substituting the expansions (18), (61), (72) in (74) and imposing (74) order by order in powers of ![]() we obtain the following formulae:
we obtain the following formulae:
![]() (75)
(75)
where the functions![]() ,
, ![]() ,
, ![]() , are given by:
, are given by:
![]() (76)
(76)
![]() (77)
(77)
Formula (75) is simply the “put-call parity” relation (74) written order by order in powers of![]() .
.
From formulae (34), (35), (36), [24] formula (19) pag. 19, formula (34) pag. 179, and [26] formula (2.32) we have:
![]() (78)
(78)
where ![]() is given by (37).
is given by (37).
From formulae (34), (35), (36), [24] formula (18) pag. 197, formula (28) pag. 146, formula 37 pag. 92, and [26] formula (2.32) we have:
![]() (79)
(79)
Substituting formulae (46), (49) in formulae (76) and (77) it follows that the functions ![]() and
and![]() ,
, ![]() , satisfy the following recursive relation:
, satisfy the following recursive relation:
![]() (80)
(80)
Substituting (79) in (80) when ![]() we have:
we have:
![]() (81)
(81)
Formulae (79), (80) and (81) imply that:
![]() (82)
(82)
From (78), (80), (81), (65), (68), (70) and (75) it is possible to obtain formulae for![]() ,
, ![]() , analogous to the formulae (65), (68), (70) obtained for
, analogous to the formulae (65), (68), (70) obtained for![]() ,
,![]() . For the terms
. For the terms![]() ,
, ![]() ,
, ![]() , expressions analogous to the ones obtained for the terms with
, expressions analogous to the ones obtained for the terms with![]() , can be deduced. These formulae become more and more involved when
, can be deduced. These formulae become more and more involved when ![]() increases and are omitted for simplicity.
increases and are omitted for simplicity.
4. The the Forward Prices/rates Moment formulae
Let us consider the moments of the forward prices/rates variable![]() ,
,![]() . Let
. Let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() be the
be the ![]() -th order moment of the forward prices/rates variable
-th order moment of the forward prices/rates variable![]() ,
, ![]() ,
, ![]() , that is:
, that is:
![]() (83)
(83)
From (11) and (18) we have:
![]() (84)
(84)
where
![]() (85)
(85)
Recall that in Section 3 we have already considered the functions ![]() and
and![]() ,
, ![]() and that these functions have been expressed with the formulae (78), (79), (80), (81).
and that these functions have been expressed with the formulae (78), (79), (80), (81).
From equations (19), (20), (21), (22), (23), (24) we obtain the following problems:
for the functions![]() ,
, ![]() , we have:
, we have:
![]() (86)
(86)
![]() (87)
(87)
![]() (88)
(88)
for the functions![]() ,
, ![]() ,
, ![]() , we have:
, we have:
![]() (89)
(89)
![]() (90)
(90)
![]() (91)
(91)
It is easy to see that:
![]() (92)
(92)
is the solution of problem (86), (87), (88) when![]() . Substituting (92) in the Equation (89) we obtain:
. Substituting (92) in the Equation (89) we obtain:
![]() (93)
(93)
Substituting formulae (92), (93) in (84) when ![]() we have:
we have:
![]() (94)
(94)
Recall that![]() . We seek
. We seek![]() ,
, ![]() , solution of problem (86), (87), (88), in the following form:
, solution of problem (86), (87), (88), in the following form:
![]() (95)
(95)
where for![]() , the index
, the index ![]() is an integer such that the function
is an integer such that the function ![]() expressed as a function of
expressed as a function of ![]() is zero when
is zero when![]() . It is easy to see that if
. It is easy to see that if![]() ,
, ![]() , satisfies the inequality:
, satisfies the inequality:
![]() (96)
(96)
the function![]() ,
, ![]() , given by (95) is zero when
, given by (95) is zero when![]() . The largest integer
. The largest integer![]() ,
, ![]() , that satisfies (96) is:
, that satisfies (96) is:
![]() (97)
(97)
where ![]() denotes the integer part of
denotes the integer part of![]() .
.
Moreover from (87) it follows that:
![]() (98)
(98)
Substituting (95) into equation (86) and equating the coefficients of the powers of ![]() of the same degree we obtain the following initial value problems:
of the same degree we obtain the following initial value problems:
for the functions![]() ,
, ![]() ,
, ![]() we have:
we have:
![]() (99)
(99)
![]() (100)
(100)
![]() (101)
(101)
![]() (102)
(102)
and
![]() (103)
(103)
![]() (104)
(104)
The solutions of the problems (99), (100) and (104), (102) are respectively:
![]() (105)
(105)
![]() (106)
(106)
and the solutions of the problems (103), (104) are:
![]() (107)
(107)
where the function:
![]() (108)
(108)
is the solution of the following problem:
![]() (109)
(109)
![]() (110)
(110)
For later convenience note that an elementary computation gives:
![]() (111)
(111)
Using equations (105), (106), (107) we obtain the following formulae:
![]() (112)
(112)
and
![]() (113)
(113)
Formula (112) reduces to (92) when![]() . In fact from (112) when
. In fact from (112) when ![]() and
and ![]() we have
we have
![]() and this last formula implies that
and this last formula implies that![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Using formulae (111), (105), (106) and (112) we have:
![]() (114)
(114)
![]() (115)
(115)
where the functions![]() ,
, ![]() , can be computed by recursion. In fact we have:
, can be computed by recursion. In fact we have:
![]() (116)
(116)
![]() (117)
(117)
![]() (118)
(118)
and recursively:
![]() (119)
(119)
Note that given (118) the integral on the right hand side of (119) that defines recursively![]() ,
,
![]() , is an elementary integral. However it is easy to see that this integration becomes cumber-
, is an elementary integral. However it is easy to see that this integration becomes cumber-
some when ![]() increases. In this case symbolic integration software tools can be used to compute the integral of (119).
increases. In this case symbolic integration software tools can be used to compute the integral of (119).
From (84), (95), (105), (106), (112) we obtain the following formula:
![]() (120)
(120)
Note that in the moment formulae (120) we have![]() . Let us deduce the moment formulae for
. Let us deduce the moment formulae for![]() .
.
We define the real variable![]() ,
, ![]() , and we express the moment
, and we express the moment
![]() ,
, ![]() , using the variables
, using the variables![]() ,
, ![]() instead of the variables
instead of the variables ![]() used up
used up
to now. For ![]() let
let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() be the
be the
moments ![]() written using the variables
written using the variables![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . From (12) it follows that the functions
. From (12) it follows that the functions![]() ,
, ![]() , satisfy the following equation:
, satisfy the following equation:
![]() (121)
(121)
with initial condition:
![]() (122)
(122)
and boundary condition:
![]() (123)
(123)
The boundary condition (123) translates to the functions![]() ,
, ![]() , the condition imposed to the variable
, the condition imposed to the variable![]() ,
, ![]() , prescribing the absorbing barrier in zero. Note that we do not consider the case
, prescribing the absorbing barrier in zero. Note that we do not consider the case ![]() because in (94) we have already shown that
because in (94) we have already shown that![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
We seek the solution of problem (121), (122), (123) in the following form:
![]() (124)
(124)
where in (124) as already imposed in (97) in the study of the case ![]() we have
we have
![]() ,.
,.
It is easy to see that from (122) it follows that the functions![]() ,
, ![]() ,
, ![]() , satisfy the initial conditions:
, satisfy the initial conditions:
![]() (125)
(125)
![]() (126)
(126)
Substituting (124) in equation (121) and equating the coefficients of the powers of ![]() of the same
of the same
degree we deduce that the functions![]() ,
, ![]() ,
, ![]() , satisfy the following initial value pro- blems:
, satisfy the following initial value pro- blems:
![]() (127)
(127)
![]() (128)
(128)
![]() (129)
(129)
![]() (130)
(130)
and
![]() (131)
(131)
![]() (132)
(132)
Using (108) and (111) it is easy to see that the functions![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , are
, are
given by:
![]() (133)
(133)
![]() (134)
(134)
![]() (135)
(135)
![]() (136)
(136)
Note that when ![]() we have
we have![]() ,
, ![]() ,
, ![]() , and that due to the recursive relation (131) this implies that
, and that due to the recursive relation (131) this implies that![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Finally substituting (133), (134), (135), (136) in (131) we have:
![]() (137)
(137)
where the functions![]() ,
, ![]() ,
, ![]() , are defined by the following recursive relation:
, are defined by the following recursive relation:
![]() (138)
(138)
![]() (139)
(139)
![]() (140)
(140)
![]() (141)
(141)
![]() (142)
(142)
The integrals contained in (142) are elementary integrals that can be computed using formula (111). The computation of these integrals is cumbersome and can be done conveniently using symbolic integration software
tools. Note that the functions![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() , are polynomials in
, are polynomials in![]() . From (124) and (137) we have:
. From (124) and (137) we have:
![]() (143)
(143)
In particular when ![]() is a positive integer formula (143) reduces to:
is a positive integer formula (143) reduces to:
![]() (144)
(144)
Formulae (94), (143), (144) are the moment formulae announced in the Introduction. These formulae are finite sums of elementary functions in particular are polynomials in ![]() and are easy to compute. They can be used in many circumstances, for example in [5] [6] similar formulae have been used to study calibration problems for the normal and lognormal SABR models.
and are easy to compute. They can be used in many circumstances, for example in [5] [6] similar formulae have been used to study calibration problems for the normal and lognormal SABR models.
5. Somenumerical experiments
In the numerical experiments presented in this Section we use the midpoint quadrature rule to approximate the integrals contained in the formulae deduced in Sections 2 and 3. Let us begin choosing the parameter values of the numerical quadratures done in the experiments.
Let![]() ,
, ![]() be positive integers and
be positive integers and![]() ,
, ![]() be positive constants, let us define:
be positive constants, let us define:
![]() (145)
(145)
![]() (146)
(146)
The points![]() ,
, ![]() , and
, and![]() ,
, ![]() , defined in (145), (146) are respectively the nodes of the midpoint quadrature rule with
, defined in (145), (146) are respectively the nodes of the midpoint quadrature rule with ![]() and
and ![]() nodes applied to the intervals
nodes applied to the intervals![]() , and
, and![]() . Let us define the functions
. Let us define the functions![]() ,
, ![]() as follows:
as follows:
![]() (147)
(147)
![]() (148)
(148)
where ![]() is the first kind modified Bessel function of order
is the first kind modified Bessel function of order![]() . We have
. We have![]() ,
, ![]() ,
, ![]() , and we choose:
, and we choose:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . We evaluate
. We evaluate
the functions ![]() and
and![]() ,
, ![]() ,
, ![]() ,
, ![]() , approximating (147), (148)
, approximating (147), (148)
using the midpoint quadrature rule in the interval ![]() in the integral in the
in the integral in the ![]() variable (i.e. (147)) and in
variable (i.e. (147)) and in
the interval ![]() in the integral in the
in the integral in the ![]() variable (i.e. (148)). We denote these approximations of
variable (i.e. (148)). We denote these approximations of![]() ,
,
![]() respectively with
respectively with ![]() and
and![]() ,
, ![]() ,
, ![]() ,
,![]() . The
. The
number of nodes![]() ,
, ![]() and the constants
and the constants![]() ,
, ![]() of the numerical quadrature are chosen in order to
of the numerical quadrature are chosen in order to
guarantee that ![]() and
and![]() ,
, ![]() ,
, ![]() ,
, ![]() , have at least six correct
, have at least six correct
significant digits.
Table 1 shows the quantity:
![]() (149)
(149)
as a function of![]() . The values of
. The values of ![]() for
for![]() , have been computed choosing
, have been computed choosing ![]() and
and ![]() (see Table 1). Recall that for
(see Table 1). Recall that for ![]() we have
we have![]() ,
, ![]() , this makes easy to deduce from the value of
, this makes easy to deduce from the value of ![]() shown in Table 1 the number of correct significant digits of the
shown in Table 1 the number of correct significant digits of the
approximation ![]() of
of![]() ,
,![]() .
.
Let us consider the quantity defined in (148) when![]() , we have
, we have![]() ,
, ![]() ,
,
![]() ,
, ![]() , moreover the numerical evaluation of (148) shows that the maximum value of
, moreover the numerical evaluation of (148) shows that the maximum value of
![]() ,
, ![]() ,
, ![]() ,
, ![]() , is approximately equal to
, is approximately equal to![]() .
.
Table 2 shows the quantity:
![]() (150)
(150)
for![]() , and has been computed choosing
, and has been computed choosing![]() ,
, ![]() in the numerical quadratures.
in the numerical quadratures.
In the experiments discussed in the rest of this Section we choose![]() ,
, ![]() ,
, ![]() ,
,![]() . We present three experiments. The first experiment investigates how the total probability of the SABR model depends from the time
. We present three experiments. The first experiment investigates how the total probability of the SABR model depends from the time ![]() when
when ![]() and from the parameters
and from the parameters ![]() and
and![]() . The second experiment investigates the convergence of the series expansion in powers of
. The second experiment investigates the convergence of the series expansion in powers of ![]() of the European put option price and verifies numerically one of the moment formulae deduced in Section 4. The third experiment introduces a calibration procedure for the SABR model based on the formulae of the option prices deduced in Section 3 and studies a time series of real data.
of the European put option price and verifies numerically one of the moment formulae deduced in Section 4. The third experiment introduces a calibration procedure for the SABR model based on the formulae of the option prices deduced in Section 3 and studies a time series of real data.
In the first experiment we begin assuming![]() . Integrating formula (39) with respect to the variables
. Integrating formula (39) with respect to the variables![]() ,
, ![]() in the domain
in the domain ![]() and choosing
and choosing![]() ,
, ![]() ,
, ![]() we have the following expression for the total probability of the SABR model:
we have the following expression for the total probability of the SABR model:
![]() (151)
(151)
where![]() ,
, ![]() , and
, and
![]() (152)
(152)
In the asset price models where the probability is conserved during the time evolution the quantity analogous to ![]() is identically equal to one. However in the SABR model considered here due to the absorbing barrier in zero imposed to the variable
is identically equal to one. However in the SABR model considered here due to the absorbing barrier in zero imposed to the variable![]() ,
, ![]() , the probability is not conserved during the time evolution. In fact the loss of total probability is monotonically increasing in time and depends from
, the probability is not conserved during the time evolution. In fact the loss of total probability is monotonically increasing in time and depends from![]() ,
,![]() . In particular, given
. In particular, given![]() , the loss of probability increases when
, the loss of probability increases when ![]() goes to zero. Furthermore formula (151) and the relation
goes to zero. Furthermore formula (151) and the relation ![]() imply that the loss of total probability increases when
imply that the loss of total probability increases when ![]() goes to one.
goes to one.
Figure 1 shows ![]() as a function of
as a function of![]() , when
, when ![]() for
for
![]() and
and![]() . In particular Figure 1 shows that the loss of total probability in the SABR model with
. In particular Figure 1 shows that the loss of total probability in the SABR model with ![]() and the absorbing barrier in zero imposed to the variable
and the absorbing barrier in zero imposed to the variable![]() ,
, ![]() , when
, when ![]() is close to one is negligible only for very small time values.
is close to one is negligible only for very small time values.
Let us consider now the total probability of the SABR model in the case ![]() and denote with
and denote with
![]() the total probability of the SABR model as a function of
the total probability of the SABR model as a function of![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() . To compute the total probability
. To compute the total probability ![]() when
when ![]() we compute the integral that gives
we compute the integral that gives ![]()
with the Monte Carlo method. This is done integrating numerically the stochastic differential equations (7), (8) with the initial conditions (9), (10). Due to the absorbing barrier in zero imposed to the variable![]() ,
, ![]() , the numerical computation of a trajectory of (7), (8), (9), (10) is stopped when the variable
, the numerical computation of a trajectory of (7), (8), (9), (10) is stopped when the variable![]() ,
, ![]() , hits zero. The numerical integration of (7), (8), (9), (10) is repeated the number of times needed to build the Monte Carlo sample necessary to approximate the integral that gives the total probability.
, hits zero. The numerical integration of (7), (8), (9), (10) is repeated the number of times needed to build the Monte Carlo sample necessary to approximate the integral that gives the total probability.
The loss of probability is measured using the quantity ![]() defined as follows:
defined as follows:
![]() (153)
(153)
where![]() ,
, ![]() ,
,![]() . Table 3 shows
. Table 3 shows ![]() as a function of
as a function of ![]() when
when![]() ,
, ![]() ,
,![]() .
.
The previous analysis shows that in practical circumstances the use for large time values of the SABR model with the absorbing barrier can lead to erroneous judgements. To address this point several authors have sug- gested the idea of adding to the probability density function studied in Section 2 some extra terms supported in ![]() to restore probability conservation. In [3] [7] [15] the large time asymptotic properties of the SABR mo- del and of several models related to the SABR model are studied and the idea of restoring probability conser- vation adding a term supported in
to restore probability conservation. In [3] [7] [15] the large time asymptotic properties of the SABR mo- del and of several models related to the SABR model are studied and the idea of restoring probability conser- vation adding a term supported in ![]() is investigated.
is investigated.
The second experiment studies the behaviour of the series expansion of the price at time ![]() of a European put option having time to maturity half a year
of a European put option having time to maturity half a year ![]() and strike price
and strike price ![]() when the values of the
when the values of the
forward prices/rates variable are generated integrating numerically the model (7), (8) with![]() ,
, ![]() ,
,
![]() , and,.
, and,.
We use the first three terms of the series expansion in powers of ![]() of the European put option price
of the European put option price ![]() that have been derived in Section 3. We denote the approximate option prices obtained in this way with
that have been derived in Section 3. We denote the approximate option prices obtained in this way with
![]() ,
, ![]() , where
, where![]() ,
, ![]() are given in (62). We
are given in (62). We
compare the prices![]() ,
, ![]() , with the price
, with the price ![]() computed evaluating (60) using the
computed evaluating (60) using the
Monte Carlo method. The trajectories of the SABR model used to sample the variables![]() ,
, ![]() in the Monte
in the Monte
Carlo computation of the option prices are obtained integrating numerically the stochastic differential equations (7), (8) with the conditions (9), (10) using the explicit Euler method with variable step-size. Note that due to the absorbing barrier in zero imposed to the forward prices/rates variable the computation of a simulated trajectory of the SABR model is stopped when the variable![]() ,
, ![]() , hits zero.
, hits zero.
We choose the size ![]() of the Monte Carlo sample using formula (82) as a test case. That is we compute
of the Monte Carlo sample using formula (82) as a test case. That is we compute
the integral in (82) using the Monte Carlo method and we denote with![]() ,
, ![]() , the result
, the result
obtained in this way. Note that for![]() ,
, ![]() ,
, ![]() , the quantity
, the quantity![]() ,
,
![]() , approximates
, approximates![]() ,
, ![]() ,
, ![]() ,
, ![]() , (see (79)). Let us define the quantity:
, (see (79)). Let us define the quantity:
![]() (154)
(154)
Table 4 shows the sample size ![]() that makes
that makes ![]() smaller than
smaller than ![]() when
when![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() , and
, and![]() ,
, ![]() ,
,![]() . In particular Table 4 shows that the accuracy of the Monte Carlo computation depends strongly from the values of the parameters
. In particular Table 4 shows that the accuracy of the Monte Carlo computation depends strongly from the values of the parameters ![]() and
and![]() . This is due to the loss of total probability that takes place during the time evolution and to the fact that this loss is particularly severe when
. This is due to the loss of total probability that takes place during the time evolution and to the fact that this loss is particularly severe when ![]() is close to one and/or
is close to one and/or ![]() is close to minus one. As suggested in Table 4 to compute the price
is close to minus one. As suggested in Table 4 to compute the price ![]() at time
at time ![]() of the previously specified option we choose the Monte Carlo sample size
of the previously specified option we choose the Monte Carlo sample size![]() . This choice guarantees that the Monte Carlo approximations of the option prices obtained in the experiment have at least three correct significant digits when the option prices considered are greater than
. This choice guarantees that the Monte Carlo approximations of the option prices obtained in the experiment have at least three correct significant digits when the option prices considered are greater than ![]() and at least two correct significant digits when the option prices considered are smaller than
and at least two correct significant digits when the option prices considered are smaller than![]() . The evaluation of one of the European put option prices considered above using a Centrino Intel Core Duo CPU T6400 processor and the Monte Carlo method with a sample of size
. The evaluation of one of the European put option prices considered above using a Centrino Intel Core Duo CPU T6400 processor and the Monte Carlo method with a sample of size ![]() takes about 500 seconds while the evaluation of formula (61) with the same processor using the midpoint quadrature rule (with the previously chosen values of the numerical integration parameters) takes 44
takes about 500 seconds while the evaluation of formula (61) with the same processor using the midpoint quadrature rule (with the previously chosen values of the numerical integration parameters) takes 44
![]()
Table 4. Monte Carlo sample size ![]() required to have
required to have![]() .
.
seconds to produce the approximate price of the put option obtained summing the first three order terms of the series expansion (61), 18 seconds to produce the price obtained summing the first two order terms and 10 se- conds to produce the price obtained using only the zero-th order term. Note that when ![]() to get two or three correct significant digits in the put option price studied it is necessary to use the first two order terms or the first three order terms of the series expansion (61) depending from the value of
to get two or three correct significant digits in the put option price studied it is necessary to use the first two order terms or the first three order terms of the series expansion (61) depending from the value of![]() .
.
Let us define the relative errors:
![]() (155)
(155)
Figure 2 shows![]() ,
, ![]() ,
, ![]() for
for![]() ,
, ![]() ,
, ![]() and
and![]() . Note that in order to guarantee that the Monte Carlo method gives at least three correct significant digits of the option prices considered we use a Monte Carlo sample size
. Note that in order to guarantee that the Monte Carlo method gives at least three correct significant digits of the option prices considered we use a Monte Carlo sample size ![]() when
when ![]() and
and ![]() when
when![]() . Figure 2 shows that the first two order terms of the expansion in powers of
. Figure 2 shows that the first two order terms of the expansion in powers of ![]() of the European put price (i.e. the approximate price
of the European put price (i.e. the approximate price![]() ) already gives a satisfactory approximation of the put price when
) already gives a satisfactory approximation of the put price when ![]() and
and![]() . More specifically the experiment shows that the mean relative errors (157) obtained using the zero-th order term, the first two order terms and the first three order terms of the expansion are respectively 0.043, 0.0319, 0.0317 when
. More specifically the experiment shows that the mean relative errors (157) obtained using the zero-th order term, the first two order terms and the first three order terms of the expansion are respectively 0.043, 0.0319, 0.0317 when ![]() and 0.131, 0.0406, 0.0296 when
and 0.131, 0.0406, 0.0296 when![]() . Figure 2 shows that the first few terms of the expansion in powers of
. Figure 2 shows that the first few terms of the expansion in powers of ![]() of the put price provide high quality ap- proximations when the put option is in the money or at the money (i.e. the forward prices/rates variable is smaller than or equal to the strike price
of the put price provide high quality ap- proximations when the put option is in the money or at the money (i.e. the forward prices/rates variable is smaller than or equal to the strike price ![]() (
(![]() in the experiment)). In fact, in this case we have that the mean relative errors are 0.046, 0.0032, 0.0031 when
in the experiment)). In fact, in this case we have that the mean relative errors are 0.046, 0.0032, 0.0031 when ![]() and 0.0267, 0.0055, 0.0033 when
and 0.0267, 0.0055, 0.0033 when![]() . Note that when
. Note that when ![]() the effect of the second order term on the computed put option price is negligible.
the effect of the second order term on the computed put option price is negligible.
Finally let us turn our attention to one of the moment formulae deduced in Section 4. Table 5 shows the mean
relative error ![]() between the theoretical second order moment
between the theoretical second order moment![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() of the forward prices/rates variable
of the forward prices/rates variable![]() ,
, ![]() , and the
, and the
simulated moment, ![]() obtained using the Monte Carlo method with a sample size
obtained using the Monte Carlo method with a sample size
![]() when
when![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , where
, where ![]() where
where
![]() ,
, ![]() ,
, ![]() ,
, ![]() , that is:
, that is:
![]() (156)
(156)
Table 5 confirms the validity of the moment formula deduced in Section 4
In the third experiment we use the SABR model to interpret real data. This is done first calibrating the SABR model using a time series of real data and then using the calibrated model to forecast option prices. Let ![]() be the five dimensional real Euclidean space, we introduce the vector
be the five dimensional real Euclidean space, we introduce the vector ![]() of the unknowns of the calibration problem and the set
of the unknowns of the calibration problem and the set ![]() of the feasible points of the calibration problem defined as
of the feasible points of the calibration problem defined as
![]()
Figure 2. Relative errors![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , maturity
, maturity![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
![]()
Table 5. Comparison between simulated and theoretical second order moments.
follows:
![]() (157)
(157)
The inequalities contained in (159) that define ![]() are the natural constraints implied by the meaning of the component of
are the natural constraints implied by the meaning of the component of ![]() in the model equations. Recall that since in the financial markets
in the model equations. Recall that since in the financial markets ![]() cannot be observed it must be regarded as a parameter to estimate in the calibration procedure and that, for simplicity, also the risk free interest rate
cannot be observed it must be regarded as a parameter to estimate in the calibration procedure and that, for simplicity, also the risk free interest rate ![]() is regarded as an unknown of the calibration problem. We use as data of the calibration pro- blem studied a set of option prices observed at a given time and we formulate the calibration problem as a non- linear constrained least squares problem.
is regarded as an unknown of the calibration problem. We use as data of the calibration pro- blem studied a set of option prices observed at a given time and we formulate the calibration problem as a non- linear constrained least squares problem.
Let![]() ,
, ![]() be positive integers,
be positive integers, ![]() be the observation time and
be the observation time and ![]() be the forward prices/rates
be the forward prices/rates
observed at time![]() . The quantities
. The quantities![]() ,
, ![]() ,
, ![]() ,
, ![]() , are
, are
respectively the observed prices at time ![]() of the European call options having maturity time
of the European call options having maturity time ![]() and
and
strike price![]() ,
, ![]() , and of the European put options having maturity time
, and of the European put options having maturity time ![]() and strike price
and strike price
![]() ,
,![]() . We assume
. We assume![]() ,
, ![]() , and
, and![]() ,
,![]() . In this experiment to
. In this experiment to
emphasize the dependence of the option prices from the parameters contained in the vector ![]() we change the notation used to represent the European call and put option prices obtained using the perturbative expansion in
we change the notation used to represent the European call and put option prices obtained using the perturbative expansion in
powers of ![]() introduced in Section 3. In fact we denote with
introduced in Section 3. In fact we denote with![]() ,
, ![]() ,
,
![]() ,
, ![]() , the prices as a function of
, the prices as a function of ![]() of the European call and put options
of the European call and put options
obtained using the first two terms of the expansion in powers of ![]() of Section 3 with the discount factors
of Section 3 with the discount factors
associated to the maturity times![]() ,
, ![]() , or
, or![]() ,
, ![]() , and we choose
, and we choose
![]() . We use only the first two terms in the power series expansion to evaluate the prices considered because the prices involved in this experiment are of the order of magnitude of cents of
. We use only the first two terms in the power series expansion to evaluate the prices considered because the prices involved in this experiment are of the order of magnitude of cents of![]() . For prices of this order of magnitude the approximate prices obtained with the first two terms of the series expansion have two correct sig- nificant digits.
. For prices of this order of magnitude the approximate prices obtained with the first two terms of the series expansion have two correct sig- nificant digits.
The calibration problem for the SABR model is formulated as follows:
![]() (158)
(158)
where the objective function ![]() is given by:
is given by:
![]() (159)
(159)
Problem (160) is the a nonlinear constrained least squares problem. This problem is solved numerically using a variable metric steepest descent method. Details about the numerical solution of problem (160) can be found in [27].
The data used in the calibration experiment are the daily values of the futures price on the EUR/USD currency exchange rate having maturity![]() , 2011, and the daily prices of the corresponding European call
, 2011, and the daily prices of the corresponding European call
and put options with expiry date![]() , 2011 and strike prices
, 2011 and strike prices![]() ,
,
![]() . The strike prices
. The strike prices![]() ,
, ![]() , are expressed in USD. The futures price on the EUR/USD currency exchange rate and the European call and put option prices are observed in the time period that goes from
, are expressed in USD. The futures price on the EUR/USD currency exchange rate and the European call and put option prices are observed in the time period that goes from![]() , 2010, to
, 2010, to![]() , 2010. The observations are daily observations and the values observed are the closing prices of the day at the New York Stock Exchange. Figure 3 shows the futures price of the EUR/USD currency exchange rate (ticker YTU1 Curncy) (solid line) and the EUR/USD currency's exchange rate (dashed line) as a function of time. Figure 4 and Figure 5 show respectively the prices (in USD) of the cor- responding European call and put options with maturity time
, 2010. The observations are daily observations and the values observed are the closing prices of the day at the New York Stock Exchange. Figure 3 shows the futures price of the EUR/USD currency exchange rate (ticker YTU1 Curncy) (solid line) and the EUR/USD currency's exchange rate (dashed line) as a function of time. Figure 4 and Figure 5 show respectively the prices (in USD) of the cor- responding European call and put options with maturity time![]() , 2011 and the previously defined strike prices
, 2011 and the previously defined strike prices![]() ,
, ![]() , as a function of time.
, as a function of time.
Specifically we choose![]() , and
, and![]() ,
,
with these choices we have ![]()
![]() . We calibrate the SABR model solving problem (160) every (trading) day during the period that goes from
. We calibrate the SABR model solving problem (160) every (trading) day during the period that goes from ![]()
![]() to
to ![]()
![]() using the prices of the European call and put options shown in Figure 4 and Figure 5 when
using the prices of the European call and put options shown in Figure 4 and Figure 5 when![]() ,
, ![]() ,
, ![]() and using the values of the forward prices/rates variables shown in Figure 3.
and using the values of the forward prices/rates variables shown in Figure 3.
Figure 6 shows the risk neutral parameters obtained using the calibration procedure described above. Recall that the maturity time of the options considered is![]() , 2011 and that the time to maturity shown in the abscissa of Figure 6, Figure 7 is the maturity time (i.e.
, 2011 and that the time to maturity shown in the abscissa of Figure 6, Figure 7 is the maturity time (i.e.![]() , 2011) minus the current time ex- pressed in (trading) days. The parameter values resulting from the calibration are shown in Figure 6 and are ap- proximately constants as functions of the time to maturity.
, 2011) minus the current time ex- pressed in (trading) days. The parameter values resulting from the calibration are shown in Figure 6 and are ap- proximately constants as functions of the time to maturity.
Next we use the values of the parameters shown in Figure 6 to forecast option prices one day ahead. That is we use the parameter values obtained calibrating the model with the data of ![]() to compute the option prices at
to compute the option prices at![]() , obtained using
, obtained using![]() ,
,![]() . The forecast option prices are obtained evaluating the European call and put option prices with the first two order terms of the expansions (72) and (61). Of course formulae (72) and (61) after being truncated must be adapted to the specific features of the data studied. Figure 7 shows the observed and the forecast values of the European call and put option prices for five different values of the strike prices:
. The forecast option prices are obtained evaluating the European call and put option prices with the first two order terms of the expansions (72) and (61). Of course formulae (72) and (61) after being truncated must be adapted to the specific features of the data studied. Figure 7 shows the observed and the forecast values of the European call and put option prices for five different values of the strike prices: ![]() (Figure 7(a)),
(Figure 7(a)), ![]() (Figure 7(b)),
(Figure 7(b)), ![]() (Figure 7(c)),
(Figure 7(c)), ![]() (Figure 7(d)),
(Figure 7(d)), ![]() (Figure 7(e)
(Figure 7(e)
![]()
Figure 3. YTU1 (solid line) and EUR/USD currency’s exchange rate (dashed line) versus time.
). In Figure 7 the option prices expressed in USD are plotted on the vertical axis that is marked with![]() , and the horizontal axis shows the time to maturity expressed in days. The time unit of the horizontal axis is the same as that of Figure 6. The average relative errors over the time interval September 27th, 2010, December 17th, 2010 on the forecast values of the European call and put option prices when compared with the corresponding prices observed in the financial market are respectively
, and the horizontal axis shows the time to maturity expressed in days. The time unit of the horizontal axis is the same as that of Figure 6. The average relative errors over the time interval September 27th, 2010, December 17th, 2010 on the forecast values of the European call and put option prices when compared with the corresponding prices observed in the financial market are respectively![]() % and
% and![]() %. These percentages reduce to 4% and 3% in the case of at the money options. Note that in this experiment we have used only one calibrated SABR model to forecast both call and put prices. More accurate results can be obtained calibrating the SABR model twice using respectively only put prices and only call prices to forecast respectively put and call prices. The two calibrated models give respectively better forecasts of put and call option prices than the forecasts obtained with the model calibrated using both call and put prices. We conclude that the third experiment shows that the SABR model
%. These percentages reduce to 4% and 3% in the case of at the money options. Note that in this experiment we have used only one calibrated SABR model to forecast both call and put prices. More accurate results can be obtained calibrating the SABR model twice using respectively only put prices and only call prices to forecast respectively put and call prices. The two calibrated models give respectively better forecasts of put and call option prices than the forecasts obtained with the model calibrated using both call and put prices. We conclude that the third experiment shows that the SABR model
interprets satisfactorily the data studied since the values of the parameters resulting from the calibration are stable (Figure 6) and the forecast option prices are accurate (Figure 7).
The website: http://www.econ.univpm.it/recchioni/finance/w18 contains auxiliary material including anima- tions, an interactive application and an app that helps the understanding of the paper.