Combining Symbolic tools with interval analysis. An application to solve robust control problems. ()
1. Introduction
The description of real systems using mathematical models has been usually concerned with the concept of uncertainty. The inaccuracies and uncertainties can be done by different causes: in the linearization of a system, for the fact that some parameters of the system can have different values for different operation conditions or because some parameters can vary with time. Moreover uncertainties are classified into two types: parametric or non-parametric. In case the origin and the structure of the uncertainty were known, they are called structured or parametric, otherwise, if they are unknown, the uncertainty is classified as unstructured or non-parametric. From a theoretical point of view, there are a lot of approaches related with parametric robust problems. Most of them use sparametric methodologies [1] -[3] . Some using QFT [4] , other Value Sets [5] .
Some of these methods have been integrated into packages as Matlab [6] or into frameworks as PARADISE [7] . All the cited approaches, manage these problems of robust control using parametric methods. Although these methods have the drawback that the solutions obtained are no guaranteed solutions.
Methods for assessing robust stability and robust design of parameter dependent linear systems, as Routh table or the small gain theorem,... give sufficient (but not always necessary) conditions to solve them. These theorems give a powerful methodology to transform robust control problems in simplified problems consisting of testing the positivity of a set of functions or conditions.
This paper presents a methodology that solves robust control problems combining symbolic computation with interval analysis [8] techniques. The main advantage of interval analysis is that it offers guaranteed solutions in case we want to solve robust control problems. Thus, its use means a really improvement in front parametric techniques.
Although the advantage of obtain guaranteed results is important, the rules and algorithms that must be generated to solve robust control problems using interval analysis, are difficult to be implemented for users. This difficulty discourage control engineers to use these techniques. This difficulty motivates us to offer the users an automatic application that uses interval techniques in a transparent way for the user. This application or framework makes a combination between symbolic tools and interval analysis methods. This paper presented his framework named IRCAD (Interval Robust Control framework for Analysis and Design) dedicated to the resolution of robust control problems applying techniques of interval analysis. This framework is composed by a set of tools of analysis and design that combine symbolic computation with the methodology of interval analysis. Thus, it is not necessary that the user have any special knowledge about interval analysis to use the functions of robust analysis and robust design that offer the framework.
The paper is organized as follows. Section 2 presents the formulation of the most typical robust parametric control problems. The use of interval analysis theory as a way to obtain guaranteed results on the solution of robust parametric control problems is the central point of Section 3. The problem of how to integrate all this diversity of data and all the involved methodologies of this kind of problems is discussed on Section 4. In Section 5 IRCAD is presented as a framework that allows the integration of the different data. Section 6 summarizes the framework and applies it to an illustrative example. Finally most emphasizing points and future intentions are put on the Section 7 of conclusions.
2. Robust Parametric Control Problem
To formulate the problem of parametric robust control we consider a system that is linear respect the variable s. This kind of systems can be expressed as a transfer function or in space state format, in continuous or in discrete domain.
In this paper we will consider a class of plants [9] with structured parametric uncertainties described by the following uncertain transfer function:
(1)
depending on a structured perturbation characterized by the parameter vector
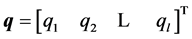(2)
where each parameter enters into the system description with polynomial dependency. We also consider a certain configuration of the feedback system with a fixed controller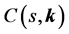
, where 
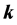is the design parameter vector. The motivation of this kind of system description is that the system parameters, q, can represent physical quantities that are known only to within a certain accuracy, or vary depending on operating conditions while the controller parameters, 
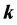, represent degrees of freedom available to the control system designer. Due to the physical interpretation of the uncertain parameters, each one can be considered independent from the other and their values lie between upper and lower bounds. Then, the uncertain domain can be defined as any hyperrectangle:
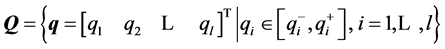(3)
With this kind of feedback system description, several robust control problems can be formulated. Problems concerning robust control analysis as testing the stability of the system or computing the stability margin. Also, problems related with control design as to find a set of controllers that fulfill one or more than one selected specifications.
2.1. Robust Control Problems: Analysis
In many control systems the plant parameters may vary over a wide range about a nominal value
. Robust parametric stability refers to the ability of a control system to maintain stability despite such large variations. Given an uncertain system and a controller, analysis of robust control problems consists in to check( calculate) some performance specifications:
Robust stability
The first problem formulated is the verification of the stability on uncertain systems. That is, how to find the necessary and sufficient conditions that allows to guarantee that a family of uncertain polynomial is stable or no. In [10] , Ackermann presents different methods to check robust stability analysis.
-Boundary crossing theorem: It is based on Hurwitz determinants. Given a set of polynomials
, this set is robustly stable, if and only if:
1) There exists a stable polynomial
2) Any root cross imaginary edge: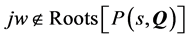 
for all 
-Alternative boundary crossing theorem based on Hurwitz Determinants [11] : Giving a set of polynomials
it is robustly stable, if and only if:
1) There exists a stable polynomial 
2) 
for all 
This work uses the just presented boundary crossing theorem in a modified way. It gives necessary and sufficient conditions of absolute robust stability for a family of characteristic polynomials.
Stability margin
If the controller is given, the parametric stability margin is defined [12] as the maximal range of variation of the parameter
, measured in a suitable norm, for which closed-loop stability is preserved. It can be expressed as:
(4)
This margin is used as a quantitative measure of the robustness of the closed loop system with respect to parametric uncertainty evaluated at the nominal point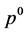
.
Parametric bode plots
Based on the experience with frequency domain analysis methods, one might conjecture that it is not necessary to check all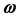 
values. Thus, it is common to construct Bode plots using only a grid of 
values. In the case of frequency domain methods for robustness analysis, the bottleneck is “singular frequencies”.
In order to provide a systematic method of identifying singular frequencies, an algebraic definition is given on [10] . Before the definition some preliminary notation is introduced. When an uncertain polynomial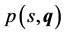 
is evaluated at a frequency 
it equals a complex number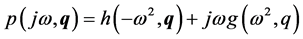
. Separating this complex number on real and imaginary parts:
(5)
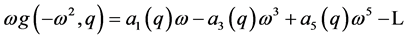(6)
Associated with these functions is a Jacobi an matrix.
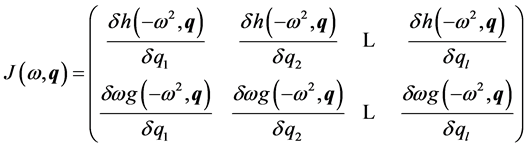
In the Jacobian
, the real part
, and the imaginary part 
are used to give algebraic definition of singular frequencies.
Definition. The nonnegative frequency ωs is a singular frequency of the uncertain polynomial 
if there exists a 
such that the three following conditions are simultaneously satisfied.
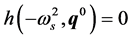(7)
(8)
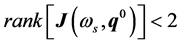(9)
The last Equation (9) can be substituted by: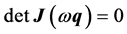 
Frequency problems
-Value sets. Some gridding approaches have as a drawback the length of time it takes to compute the set of frequency plots. An alternative and faster technique, suggested in [5] , is to compute the frequency plot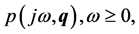 
for each 
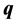on a grid of
. It is advisable to compute the value set for each 
on a grid of frequencies from 0 to +∞.
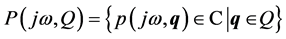(10)
In the case of a family of polynomials, the stability test is based on repeating the construction of the value set for a grid of frequencies to give the set of all possible frequency plots. The collection of value sets would then indicate stability or instability depending on how the zero-exclusion theorem is formulated.
Theorem 1. (zero-exclusion theorem). Given a polynomial family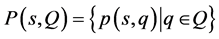
. This set is robustly stable if and only if
- A stable polynomial 
exists and
- 
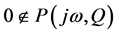for all
.
Discrete-time problems
Some problems concerned with discrete-time are:
-Model conversion. Conversion is needed in both senses, from a continuous time interval state-space model to a discrete-time interval model and also from a discrete-time uncertain system to a continuous-time uncertain model.
-Schur stability test. The problem of checking the stability of a discrete-time system is reduced to the determination of whether or not the roots of the characteristic polynomial of the system lie strictly within the unit disc, that is whether or not the characteristic polynomial is a Schur polynomial. If
, (11)
where the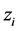 
are the n roots of 
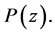Then if 
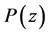is Schur, all these roots are located inside the unit circle 
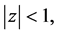so that when 
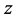varies along the unit circle
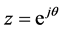, the argument of 
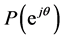increases monotonically. For a Schur polynomial of degree n, 
has a net increase of argument of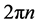
, and thus the plot of 
encircles the origin n times. This can be used as frequency domain test for Schur stability [13] [14] .
-Non-linear discrete-time control of uncertain systems. This problem can be formulated as:
Find one c
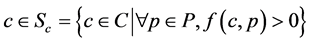(12)
where f is a vector function that can be evaluated using algorithms based on interval analysis. This problem is both quite complex because it involves a quantifier and, at the same time, very simple because the only objective is to find one feasible vector. This makes considering a larger number of tuning parameters corresponding to the guaranteed-tuning problem [15] . This is evidence that it is possible to combine non-linearity, and structured uncertainty with guaranteed results.
2.2. Robust Control Problems Design
The requirement of robust design is that the design specifications must be satisfied over the entire parameter set. Given an uncertain system, the problem is to obtain a robust controller that fulfills some performance specifications.
As robust performance specifications we can enumerate stability, pole locations, steady-state, 
, etc. It is known that the solution of these problems can be reduced to the problem of checking the positivity of a set of rational functions over a given domain:
(13)
where 
is the generalized frequency and 
may be a single point (nominal controller
) or a certain domain in the parameter’s space of the controller depending on the problem considered.
Robustness analysis: to check if the controlled system achieves robust performances.
(14)
Robust control design: to find the robust K set such that the controlled system achieves robust performances.
(15)
Most of the more used robust control design techniques are based on the worst possible scenario which may never occur in a particular control system. Some of these techniques are the following:
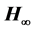control [16] . Robust performance specifications may be given as pole locations as well as 
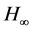performances expressed in the frequency domain.
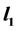control [17] . In the standard 
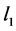problem the design of an internally stabilizing controller such that the 
norm of the regulated output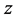 
due to the worst-case magnitude bounded disturbance 
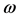is addressed. The Banach space of right-sided absolutely summable real sequences with the norm given by
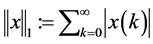(16)
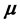synthesis. It minimizes the superior bound of the robust performance. The criterion is
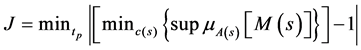(17)
where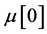 
is the structured singular value, 
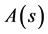is the disturbance matrix which indicates that 
depends on the allowed structure for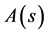
, 
is a matrix obtained by rearranging the uncertain system into the M A-structure and 
indicates that the minimisation is function of the controller parameters [18] [19] .
QFT (Quantitative feedback theory). While value sets are mainly concerned with analysis, when the aim is finding a compensator to satisfy design specifications, QFT is the most important approach. It can be considered as a natural extension of classical frequency-domain design approaches. One of the main objectives is to design a simple low-order controller where the bandwidth of the feedback controller being as small as possible. At a fixed frequency, the plant’s frequency response set is called a template. In the bound generation step of QFT design procedure, the plant template is used to translate the given robustness specifications in domains in the Nichols chart where the controller gain-phase values are allowed to lie.
We are focused on the solution of robust control design problems. That is, we are testing if a controller K achieves the design specifications.
Some applications can be found in the design field. Parameter spaces of the controller are explored, finding the regions which fulfill a control specification in order to obtain a controller which satisfies it.
3. Interval Formulation of Robust Parametric Control
The problem of robust parametric control, presented on the last section, is now formulated using interval analysis. Using the theory of interval analysis is possible to obtain guaranteed solutions to robust control problems. To formulate these problems on interval format, we formulate the problem of the parameter space approach considering the uncertain system of Figure 1, where k is the parameter vector of the controller,
(18)
q is the parameter vector of the process, and the uncertainty domain can be defined as a box:
(19)
Design specifications are formulated in terms of closed-loop system stability and performances in the frequency domain. These specifications, such as bandwidth, resonance peak, control effort, etc., can be described as a set of N inequalities of the type:
(20)
where Ω is a subset of ℝ+ (usually an interval), Q an interval vector representing interval parameters and K; a nondegenerate set.
Then robust design can be formulated as follows: given a controller structure, C(s, K) the aim is to find the values of k which conform with the robust control specifications. Taking this formulation into account some control problems can be proposed [20] :
1) Performance checking. Given the uncertain system 
and the uncertain domain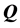
, the problem is to test if the designed controller 
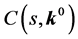achieve the robustness specifications obtained from Equation (20):
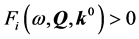(21)
2) Performance margin computation. Taking set ∏ as a function of its radius
:
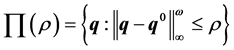(22)
find the maximal set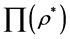 
so that the designed controller 
achieves robust performances for all 
belonging to
.
3) Robust controller design. Taking a particular structure for the controller and specifying the uncertain domain where the parameters of the system 
can vary, find a fixed structure controller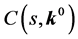 
so the controlled closed loop system achieves the robust performance specifications:
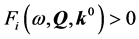(23)
4) Obtaining the set K for the robust controller problem. Given an uncertain plant 
the variation domain of the system parameter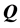 
and a controller structure, find the robust set 
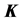which allows 
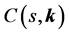to achieve the robustness specifications:
(24)
5) Estimating the stability region problem, for a given
. This problem consists on building a set of all 
‘s achieves closed loop stability when given
.
In our approach two robust control problems, Design and Analysis, have been converted into a set of functions using symbolic computation. These functions have been intervalised resulting on a set of interval functions. At this point, to solve the problems it has only been necessary to test the positivity of these interval functions for all the variation of its parameters, Equation (14) and Equation (15).
4. Integration of Numeric, Interval and Symbolic Computation
As it has seen in Section 2, problems related with robust parametric control systems use symbolic data due these systems involves uncertain variables. Moreover in Section 3 is denoted that the interval formulation of the problems involves numeric and interval data. Thus, solving robust control problems using interval analysis tools, offer guaranteed results, but as a drawback, its use requires the interaction with multiple kind of data. These difficulties can discourage control engineers to use interval techniques although its benefits.
To make all these tools and techniques more available is interesting an environment that integrates the treatment of all these kind of data, allowing deal with robust control problems, solving them using a common methodology.
In this sense our work has found how to offer to the control engineer a set of friendly user interface tools that integrates the diversity of data that these kinds of problems involves and also allows to use interval tools in a transparent way for the user.
In Figure 2, a schema of the different tools used for these kinds of problems to manage numeric symbolic and interval computation is shown.
As it can be seen in this schema, Matlab is the package used to centralize our environment. It is the selected package to develop the most routines of our environment due three main points:
- The high computational power with problems that involves matrix data.
- Its facility to deal with high level languages.
- Its easy connection with other commercial packages as Maple.
Our framework solves robust control problems, thus, problems that have implicitly high level degree of computation. This aspect would be a bottleneck if they would be solved writing scripts on a package like Matlab. Due this high cost of computation the routines on this framework have been implemented with the high level language C++. This language improves the building of procedures which require numeric-interval computation and allows to execute code in a faster way than using Matlab. This achievement was very decisive. In addition it allows to use tools from interval analysis libraries [21] , due its include instructions.
Once presented the two main packages used by the framework, it rests to say how Matlab procedures link with C++ critical routines. The deal of procedures and data among these two packages is done using code CMEX and DLL functions. The high level C++ functions are compiled using Borland, obtaining a set of dll function. There are executable functions that can be called from Matlab commands or from Matlab scripts.
Another aspect to consider is how to enter symbolic data, such as transfer functions or problem specifications. In our case it has been choose the Maple package. The extraction of these symbolic inputs from Matlab scripts and the pass of them to the Maple Package are implemented using the Symbolic Math Toolbox.
Therefore, Matlab is used to make the integration of numeric, interval and symbolic data, taking symbolic inputs, transforming them into a suitable format for the C++ routines, passing these transformed inputs to the C++ routines and finally collecting the data returned.
The last step, shown in the lower part of the diagram (user interface block) corresponds to the need to show results in a suitable way for control applications. The framework has implemented this part using the GUI-tools of Matlab. These tools allow to achieve a friendly interface that allows to present the results in an adequate format to be analyzed easily by the user.
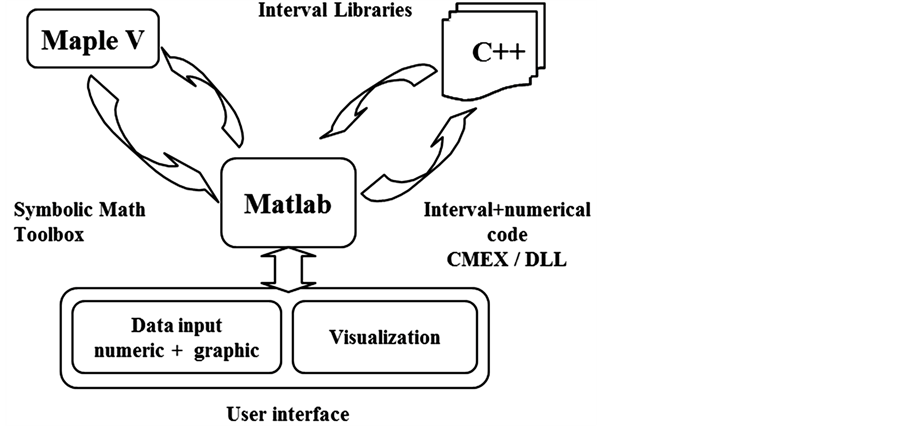
Figure 2. Cooperation numeric-interval-symbolic.
5. IRCAD: A Framework for Robust Control Problems
Once introduced the need to integrate the diversity of data and methods in section 4, now in this section we present the developed environment in order to achieve this integration. To obtain the kindly manipulation of numeric, interval and symbolic computation, our work has built a set of tools under the format of a framework called IRCAD (Interval Robust Control framework for Analysis and Design). To introduce the framework IRCAD (main screen is showed on Figure 3), we present the functions that it integrates. These functions or tools could be laid as three sets of problems.
The first set includes robust analysis problems like to test the stability of a system and to find the stability margin. The second set of problems are related to robust design problems and the main tool is an application that allows to select the design specifications that we want our control system achieve. The framework includes a third set corresponding to post-design tools, which allows that a selected controller can be applied to the system without leave the framework IRCAD.
The starting point to use the tools of the framework is to input the transfer function of the plant. Due the systems we consider are uncertain systems, the plant is defined as a family of transfer functions. To input them into the framework it is necessary to define a transfer function with undefined parameters, and also define their uncertain values range (interval values). So, as example, we can define a transfer function for a family of plants like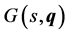 
with the uncertain parameter
.
5.1. Tools for Robust Analysis
The framework IRCAD has a set of tools addressed to solve robust analysis problems. Giving an uncertain system, where the transfer function is defined as a family of plants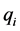
, from the menu Analysis, it is possible to make the following functions:
-Stability test. To calculate the absolute stability region, a branch-and-bound algorithm based on interval analysis is used. The result of this tool shows the regions stable and unstable. In case the depth of the algorithms was limited (in order to accelerate the end of the computation) can appear undefined regions. In the case there aren’t problems of time computation, due the computer has high computation resources, it is possible to don’t limit the depth of search and then the lonely regions that appear are estable and unestable regions.
-Stability margin computation. The parametric stability margin is defined as the length of the smallest perturbation 
which destabilizes the closed loop. This margin is used as a quantitative measure of the robustness of the closed loop system with respect to parametric uncertainty evaluated at the nominal point
.
-Parametric Bode plots. It is common to construct Bode plots using only a grid of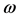 
values. There are, however, cases when ‘singular frequencies’ occur. The framework considers these cases which require special attention in all frequency domain methods for robustness analysis.
5.2. Tools for Robust Design
The IRCAD framework has a powerful set of tools aimed at the design of controllers in the case of parametric control systems. Given an uncertain system, where the transfer function is defined as a family of plants
, from the menu design it is possible to select one or more than one specification. The specifications involve temporal and frequency domain and include: stability degree, absolute stability, resonance peak, velocity error, settling time, control effort and overshoot.
Once the specifications have been selected, each chosen specification is translated to an interval function, converting them into matrix structures and passing them to a solver (a C++ routine). The results of the solver routine, that is to say the results of the design problem, are returned on a matrix format as a set of controllers that fulfill the selected specification or the set of specifications. The resultant controllers are a set of interval values. Using the tools of Graphic User Interface from Matlab (GUI tools), the resultant matrix, which contains all the information about the valid controllers is passed to the user.
The framework allows to choose in which format we want to show the set of valid controllers. It is possible to visualize this set in a graphic way or in a numeric way. The decision often depends on the number of parameters selected for the controller. If the user wants to design a controller of two or less parameters, he can choose the graphical format, then the result will be a graph with the parameter space ranged by the parameters of the controller 
In this graph the set of valid controllers are colored as a red region (Figure 5), the unfeasible controllers on a yellow region and the undefined regions on blue regions. If the user choose to obtain the set of valid controllers in a numeric format, then the framework shows on a table, the set of intervals for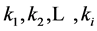 
that allows the system fulfill all the specifications.
5.3. Post-Design Tools
To help control engineer, IRCAD framework offers a very complete and power fulset of post-design functions. These functions allow the user, on the one hand to complete the design selecting one interval controller from the feasible controller set and in the other hand allow to verify that the selected controller achieve the specifications, without exit from application.
In order to offer a more reliable framework, the package gives the possibility to choose a criterion to select the optimal controller.
-Optimal Controller. The results of the robust control problem design are returned as a set of controllers that fulfill the specification or the set of specifications selected. To choose the optimal controller among this set is a task that can be not easy for the user, although the user was control engineer. To make the selection of the optimal controller from the given set of feasible controllers computed by the framework IRCAD, that offers the possibility to do it using three different criteria:
Minimum norm: Given a graphical region of feasible controllers, in the parameter space delimited by the parameters of the controller 
and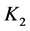
, this criteria select the interval controller 
that, fulfilling the specifications, has the minimum norm. This measure is calculated from the origin of the parameter space to the square defined by the interval
.
Maximum robustness: In this case the framework computes over each square 
the value of the stability margin and selects as controller the square 
that have the maximum value.
Neighboring: Over each feasible square
, the interval controller, the framework computes the number of neighbors. The square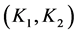 
with the maximum number of neighbors is selected.
When the user selects one of these criteria, then IRCAD computes one recommended controller following the method chosen. The framework shows the obtained controller by two ways at time: graphically and numerically. Graphically, emphasizing this controller with a dark color on the graphic, that represents the set of feasible controllers (Figure 6), and Numerically, where is opened a window with the recommended values for the controller.
The recommended value for the controller can be introduced on the controller box as an entry, or it can be introduced automatically as following is explained.
-Input optimal controller. The framework allows that the parameters of the commended controller obtained using one of the techniques exposed (minimum norm, maximum robustness or nearest neighbor) can directly be input. This automatic entry of the parameters of the controller allows to execute post-design tasks without exit from the framework.
-Post design tools. It is not necessary to go to any simulation environment to verify the selection, because the selected controller can be simulated using the same framework IRCAD.
All these features give to the user a friendly environment to work in the case of robust control problems, with the security that he has obtained guarantee solutions on the results.
The mainly tools of this block are concerning to the facilities to have tools to check that a designed controller fulfill a set of specifications.
6. Illustrative Example
To illustrate how the solver created manages the data, an example suggested by [22] and later studied by [23] is used. The aim of the example is tuning a PI controller for an interval plant.
Example 1. Robust control design.
Given the transfer function of the plant:
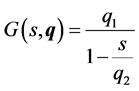(25)
where q is the vector of uncertain parameters , 
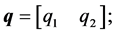and the PI controller is described by:
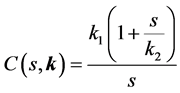(26)
where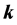 
is the vector of the design parameters,
.
The design aim is to find the set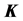 
of controller parameters that fulfill the following performance specifications:
1. Absolute stability.
2. Velocity error lower than 2%.
3. Resonance peak lower than 3 dB.
4. Control effort lower than 20.
Given the Equation (26), the toolbox IRCAD manage each one of these specifications transforming them via the Extended Symbolic Toolbox into a set of polynomial interval functions [Equations (27)-(30)]. Matlab send these functions to the solver, transforming it previously on a matrix structure. This transformation is automatically done by IRCAD toolbox, thus it is transparent to the user. The role of the solver is to test the positivity of these functions over the parameter space, which is determined by the controller parameters. In this example the parameter space is determined by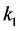 
and
. IRCAD allows to present the results of the solver in two formats :
-Graphically.
-Set of intervals.
For this example the parameter space to be checked is limited giving the initial interval values to the parameters of the controller as 
and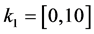
. In order to work with positive intervals the change 
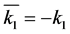has been made.
As is exposed at Section 2, in the subsection dedicated to robust control problems of design, to test if one specification or a set of specifications are fulfilled it is enough to test if a function or a set of functions are positive. In our example it is enough to test the positivity of the following functions:
1) For the specification of absolute stability the function obtained is:
(27)
2) For the specification of velocity error less than 2%:
(28)
3) For the specification of resonance peak lower than 3 dB:
(29)
4) And finally for control effort lower than 20:
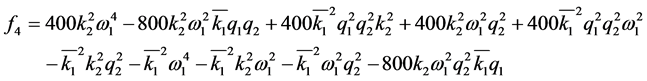(30)
The resultant feasible regions for each specification are represented on Figure 4.
In this example, specification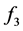 
and specially specification 
have a hard computation cost due its high number of summand components and also for the high number of plant variables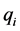 
and controller variables 
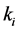that they involve.
Although this, when IRCAD compute the four specifications at the same time the cost of computation is significantly reduced because some regions are discarded on the specification of lost cost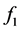 
and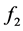
.
Using IRCAD, the problem of design a controller that fulfills the four specifications gives the graphical classification of Figure 5.
The graphical result of Figure 5 corresponds to the following set of feasible intervals:
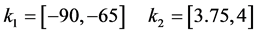
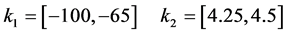
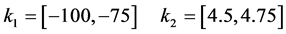
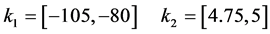
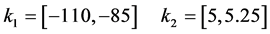
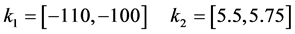
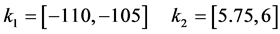
Finally, the solution of this robust control design example consists on the choice from this feasible region, following some criterion, of an interval pair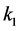 
and 
for the PI controller.
At this point IRCAD offers a set of post-design tools that allows to choose the optimal controller from the set of the proposed controllers on an automatic way. The framework chooses the controller following the criteria (see Section 5.3) that the user has selected.
In this example we suppose the user select the criterion of minimum norm. Then the controller suggested by the framework IRCAD is 
as is shown on Figure 6.
This action gives the optimal controller that fulfills the set of specifications. Using another post-design tool of the framework, the user can put this optimal controller on the closed-loop system. Finally, with this controller and this plant the framework offers some post design tools to simulate the features of the system.
7. Conclusions and Future Work
An application to solve robust control problems was designed combining symbolic tools with interval analysis. The main advantage of using interval analysis is that guaranteed results are obtained. The drawback is the ne-
cessity to work with a variety of data, implicit on these kinds of problems. It is necessary to manage symbolic, interval and numeric data. The manipulation of these kinds of data needs to use the fitting software in each case. This diversity can discourage control engineers because most of them don’t use these data in a mixed way. The framework created, allows users to manage on an easy way with problems that involves these kinds of data in a transparent way. The result is a most reliable framework for control engineers to solve problems that involves symbolic-interval-numeric data.