Survival Analysis in Modeling the Birth Interval of the First Child in Indonesia ()
1. Introduction
In demography, there are three things which take effect, namely mortality, migration, and fertility. The birth interval of the first child can be used as one of indicators of fertility. The birth interval of the first child is defined as difference between the age of marriage and the age of birth of the first child. In fact, the length of birth interval of the first child of every married woman is not same. According to existing research, the birth interval of the first child is determined by many kinds of social and culture even physiology factors. According to [1] , there are several factors that affect the birth interval of the first child, which are the area of residence, educational level, age, the knowledge of contraception and employment status. Most of married women have given birth to their first child a couple months right after the marriage, so that the obtained data are the complete one, but the others who do not have children yet are classified as the censored data. Thus the birth interval of the first child is an example of the survival data. The survival data are the data that indicate the period of time since the initial observation to a happened event. The characteristic of the survival data is its survival time, which usually could not be fully observed (censored) [2] . If all the expected events have happened, and are able to be fully observed, some analysis methods can be done; unfortunately, the survival data are censored [3] . Analyzing the survival data using the ordinary method would be inappropriate because of causing bias [4] . A certain method to analyze it was needed for reducing such bias. This certain method is called survival analysis.
2. Definitions Associated with Survival Analysis
Definition 1: Survival time measures the period of time from the initial event to happened event such as failure, death, respond, symptoms, and etc. [5] .
Definition 2: Survival function is a function indicates the probability of an individual who survives until or more than t time (experiencing the event after t time) [6] . Consider random variable T, then the survival function define as,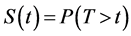 . Consider f as the probability density function, then the survival function also defines as complement of cumulative function F as,
. Consider f as the probability density function, then the survival function also defines as complement of cumulative function F as,
 [7]
[7]
Definition 3: Hazard function is a function indicates the probability of an individual of having risk or experiencing event such as failure or die at t time in the condition that this individual survived to t time, the function given by:
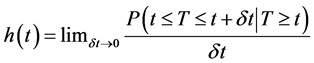 [8]
[8]
From those definitions above, the relation between the survival function and hazard function are obtained.
Using the definition of the conditional probability, obtained:
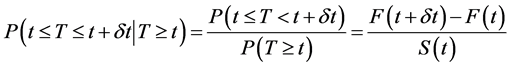
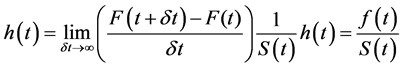
Since 
Then 
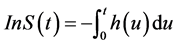
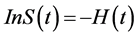
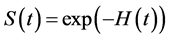
3. Model
In this research, there are two survival methods that will be used, i.e. exponential parametric and non-parametric method.
3.1. Parametric Method
Survival time can be analyzed by using the accelerated failure time (AFT) model. In the survival time, this model assumes that the logarithm relation of survival time T and its covariates are linear and can be written as
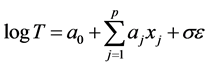
where 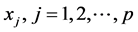 indicate its covariates,
indicate its covariates, 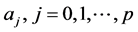 coefficient of
coefficient of  indicates the scale parameter and
indicates the scale parameter and 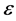 indicates the error.
indicates the error.
[9] states that for inclusion of covariates in the exponential distribution, we use the equation above and choose 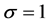 to obtain
to obtain
![]()
where![]() . T is the exponential distribution with hazard function, probability density function, and survival function respectively
. T is the exponential distribution with hazard function, probability density function, and survival function respectively
![]()
![]()
![]()
3.2. Non-Parametric Method
3.2.1. Kaplan-Meier Model
In the Kaplan-Meier method, assuming the distribution of the data is discrete. According to [10] , Kaplan-Meier is a method used to compare the survival time of two covariate groups. The advantage of this method is that the non-parametric method does not require the knowledge of a particular distribution [11] .
This method is appropriate because the data used are the individual data, but still appropriate for small, medium and large data sizes. Suppose the time of the birth of the first child denotes by r and the number of women who are married denotes by n, where r ≤ n. The probability of the birth of the first child in every interval j esti-
mated by![]() , and its survival probability estimated by
, and its survival probability estimated by ![]() The estimator for survival function of Kaplan-Meier method is given by,
The estimator for survival function of Kaplan-Meier method is given by,
![]()
where ![]()
![]()
3.2.2. Cox Proportional Hazard and Non-Proportional Hazard Model
Cox proportional hazard is a model usually used as multivariate approach to analyze the data [12] . The characteristic of Cox proportional hazard model indicates that every different individual has proportional hazard func- tion, that is, ![]() , the ratio of the hazard function of two individuals with the inclusion of cova-
, the ratio of the hazard function of two individuals with the inclusion of cova-
riates ![]() and
and ![]() are constant. This means that the ratio of failure risk of two individuals is the same and does not depend on how long they survived.
are constant. This means that the ratio of failure risk of two individuals is the same and does not depend on how long they survived.
[13] explains that the general form of Cox proportional hazard model is:
![]() .
.
where x denotes covariate, but he did not make any assumptions about the form of ![]() itself, which is called the baseline of hazard function, because it is the value of hazard function when
itself, which is called the baseline of hazard function, because it is the value of hazard function when ![]()
Sometimes the time-dependent covariate was found, so it is not met with the proportional assumption, then the form above was developed into Cox extended model:
![]()
For checking the proportional assumption of covariate, the Cox extended model can be written as:
![]()
where ![]() denotes function of time and it is important to determine the proper form of
denotes function of time and it is important to determine the proper form of ![]() The following possibilities of a function
The following possibilities of a function ![]() according to [14] are:
according to [14] are:
1) ![]() is the simplest form by resulting the Coxproportinal hazard model.
is the simplest form by resulting the Coxproportinal hazard model.
2)![]() . If the test result
. If the test result ![]() is significant then the Cox extended model is better than the Cox proportional hazard model, thus the ratio of hazard function is a function of time.
is significant then the Cox extended model is better than the Cox proportional hazard model, thus the ratio of hazard function is a function of time.
3) ![]()
4) ![]() heavyside function. When this function is used then obtained the constant of hazard ratio for different time intervals.
heavyside function. When this function is used then obtained the constant of hazard ratio for different time intervals.
4. Parameter Estimation
In estimating parameter ![]() Cox using the maximum likelihood estimation method (the maximum likelihood estimator) by only considering the individual probability who are experiencing the event called partial likelihood [14] . Estimation
Cox using the maximum likelihood estimation method (the maximum likelihood estimator) by only considering the individual probability who are experiencing the event called partial likelihood [14] . Estimation ![]() using partial likelihood means maximizing the partial likelihood function. Partial likelihood function is the joint probability survival function of uncensored data formed by the function of unknown value of parameter. [7] stated that parameter estimation
using partial likelihood means maximizing the partial likelihood function. Partial likelihood function is the joint probability survival function of uncensored data formed by the function of unknown value of parameter. [7] stated that parameter estimation ![]() can be proved by taking survival individual cases such as the death event. Suppose there are n individuals with r individuals who are having death then there exist
can be proved by taking survival individual cases such as the death event. Suppose there are n individuals with r individuals who are having death then there exist ![]() individuals censored. Assumed that there is only an individual who died at a certain time of death (there is no ties). Again suppose that
individuals censored. Assumed that there is only an individual who died at a certain time of death (there is no ties). Again suppose that ![]() is the ordered and uncensored survival time. The probability of the i-th individual death at time
is the ordered and uncensored survival time. The probability of the i-th individual death at time ![]() in terms of
in terms of ![]() as the only exact time of death of
as the only exact time of death of ![]() and the covariate for died individual at time
and the covariate for died individual at time ![]() is
is ![]() denote as:
denote as:
![]()
The numerator indicates the i-th individual death risk at time![]() , denotes as
, denotes as![]() , while the denominator indicates the number of death risk at time
, while the denominator indicates the number of death risk at time ![]() for all individual who had death risk at
for all individual who had death risk at ![]() or its sum
or its sum ![]() in
in![]() , where
, where ![]() is the set of individual who had risk of death at time
is the set of individual who had risk of death at time![]() , that is individuals who lived and uncensored just before
, that is individuals who lived and uncensored just before ![]() so that
so that ![]() called the risk set. Suppose A is the i-th individual event with covariate
called the risk set. Suppose A is the i-th individual event with covariate ![]() died at time
died at time ![]() and B is the single death event at time
and B is the single death event at time![]() . The above equation becomes
. The above equation becomes
![]() .
.
By substituting equation in Cox proportional hazard model obtained
![]() .
.
Thus the likelihood function of the conditional probability above is
![]()
where ![]() is a covariate vector for individual who died at time
is a covariate vector for individual who died at time![]() . The amount of
. The amount of ![]() re-
re-
present the sum of ![]() for every element of individual
for every element of individual![]() . Multiplication in the likelihood function only for uncensored individual. The censored individual excluding in the numerator but in the denominator is the sum of
. Multiplication in the likelihood function only for uncensored individual. The censored individual excluding in the numerator but in the denominator is the sum of ![]() for every l element of
for every l element of![]() .
.
Suppose that the data consist of n observation of survival time ![]() and
and ![]() denotes the indicator of event by valued
denotes the indicator of event by valued
![]()
Then the equation of likelihood function can be written as
![]()
If this equation turned to be logarithm then obtained
![]()
Parameter estimator ![]() can be obtained by maximizing the log function
can be obtained by maximizing the log function![]() , so that the solution be
, so that the solution be
![]()
The solution of such equation is hardly solved analytically but more easily solved using numeric method.
5. Data
The data used in this research taken from the result of Indonesia Demographic and Health Survey in 2002. The samples used are the data of two provinces, that are West Papua and Special Area of Yogyakarta as representation of high and low fertility level area. The data limited to the birth interval of the first child, of first time married woman.
6. Operational Definition
The dependent variable used in this research is the birth interval of the first child of a first time married woman. Whereas the independent variables that estimated to affect the birth interval of the first child are:
1) Area of residence, grouped in the smallest administrative unit of area, that are urban and countryside area. The area of residence divided into two categories, that are city = 1 and village = 2.
2) Education, schools are the formal schools start from the primary, junior, and high school, including the equated education. Those who never sign into formal education or ever been in primary school but never getting a passing mark are classified as not finished the primary school. The highest education divided into four categories, that are not finished the primary school = 0, finished the primary school = 1, finished the junior high school = 2, and finished the senior high school or higher = 3.
3) Employment status, working is the activity of doing the job with purpose of obtaining or earning income or profit for at least one hour per week continuously and uninterrupted (including as unpaid family workers who helped in the business/economic activity). Employment status are categorized into unemployment = 0 and employment = 1.
4) Knowledge about contraception, divided by two categories, unknown = 0 and known = 1.
5) Age of mother, age of mother/first time married woman expressed in years.
7. Results
The Kolmogorov-Smirnov goodness of fit test can be applied to test whether a sample theoretically follows a population distribution. Based on the calculating results obtained that the value of D = 0.258 and the critical value of table D* for significance level 0.05 is 0.04025. Since the calculating value of D is greater than the critical value of table D then reject H0, which means that the data is not exponentially distributed. Furthermore, since the data of birth interval of the first child is not exponentially distributed then the exponential method is not used for analyzing the factors that supposed dominantly affecting the birth interval of the first child.
As an illustration, the birth interval data of the first child will be analyzed using the Kaplan-Meier method. Its respond variable is the time of marriage to the time of having the first child and the area of residence is the variable that affect the survival level (0 = village, 1 = city).
The survival analysis results using the Kaplan-Meier method for independent area of residence of variable can be shown in graphic as follows.
From Figure 1 shown that the survived individual who lived in the villages are different with those who lived in the cities. Next the hypothesis test will be conducted to see whether this difference significantly affect or just coincidence, by the following hypothesis,
![]()
If the log rank ![]() is the statistic test value then the rejection area is H0. The log rank test results based on the area of residence covariate status are presented in the Table 1.
is the statistic test value then the rejection area is H0. The log rank test results based on the area of residence covariate status are presented in the Table 1.
By using the significance level 0.05 of chi-square test with degree of freedom 1 obtained W value significant enough to reject H0. So, it can be concluded that there is significantly difference among the survival level of the birth of the first child, who lived in the village and in the city.
If the survival data that will be compared are comes from more than two individual groups, e.g. we are interested in seeing the characteristic difference of the area of residence, education level, age, knowledge about contraception and so forth, then the Kaplan-Meier method will be impractical. This caused of in the Kaplan-Meier method, every two of population groups must be tested separately, so if there are several groups then repeated testing must be conducted. If the respondents have several characteristics, then the Cox proportional hazard method able to explain the influence of such characteristics to the respond variables simultaneously.
Table 2 shows that the explanatory variables significantly affected to the interval birth of the first child are the area of residence, education 1, education 2, education 3, and age.
![]()
Figure 1. Survival function of Kaplan-Meier method for independent area of residence variables.
![]()
Table 1. The log rank test result to see the difference of the survival level of the birth of the first child based on the area of residence covariate.
![]()
Table 2. Correlation and p-value of explanatory variables.
Next the estimation to the proportional assumption of every covariate was done. In this paper, the only method used to check the covariate that does not met the proportional assumption in the birth interval of the first child is Schoenfeld residuals method. The results are presented in Table 2.
The covariate of p-value of individual aged less than 0.05 means there is correlation between such covariate to the time rating until that individual had her first child, so that the age covariate does not met the proportional assumption. Thus the data re-modeled using the Cox extended model. Before the analysis is done, conducted the test previously to see more appropriate form of![]() . This test uses the AIC criteria. The AIC is a measure for selecting the best regression model, introduced by Hirotugu Akaike in 1973. The AIC method is based on the maximum likelihood estimation [15] , with the equation as follows
. This test uses the AIC criteria. The AIC is a measure for selecting the best regression model, introduced by Hirotugu Akaike in 1973. The AIC method is based on the maximum likelihood estimation [15] , with the equation as follows
![]()
where ![]() indicates the likelihood function, q indicates the sum of parameter
indicates the likelihood function, q indicates the sum of parameter![]() , and
, and ![]() indicates the specified constant. The value of
indicates the specified constant. The value of ![]() that often used is between 2 and 6. Based on the AIC method, the best regression model is the model that has the smallest value of AIC [9] .
that often used is between 2 and 6. Based on the AIC method, the best regression model is the model that has the smallest value of AIC [9] .
The value of AIC formed in ![]() is the smallest among the two other models (Table 3). Thus this is the best model.
is the smallest among the two other models (Table 3). Thus this is the best model.
Next the test was done to see significantly affected covariate to the respond variable. The results are presented in Table 4.
In Table 4 seen that the explanatory variables that significantly affect to the birth interval of the first child are the area of residence, education 1, education 2, education 3, and age.
8. Interpretation
The value of hazard ratio allows us to compare among multiple groups in the survival analysis [16] . Table 5 shows that the area of residence, education 1, education 2, education 3, and age variables are significantly affect to the individual risk of having first child. From the value of hazard ratio seen that individual who lived in the city had 0.720 times lower risk of having their first child than who lived in village one, and the educational history of individual who finished their primary, junior, senior high school or higher will increase the risk of having their first child respectively 1.708, 2.648, 4.361 times of individual who had lower educational history or not finished their primary school at all. Every additional age of one year will reduce the risk of having first child as 4.5%.
Table 4 shows that the area of residence, education 1, education 2, education 3, and age variables are the significantly affected to the individual risk of having her first child. From the value of hazard ratio seen that individual who lived in the city had 0.719 times lower risk of having their first child than who lived in village one,
![]()
Table 4. Parameter estimator, p-value, and the hazard ratio by using the cox extended model.
![]()
Table 5. Parameter estimator, p-value, and hazard ratio using cox proportional hazard model.
and the educational history of individual who finished her primary, junior, senior high school or higher will increase the risk of having their first child respectively 1.730, 2.648, 4.235 times of individual who had lower educational history or not finished their primary school at all. Every additional age of one year will reduce the risk of having first child as 3.0166%.
9. Conclusions
The result of distribution tests by using the Kolmogorov-Smirnov test indicates that the data do not have a particular distribution, so the Cox proportional hazard model of non-parametric method is a more appropriate method for modeling the birth interval data of the first child. However, after testing the assumption of proportional hazard model, it turned out that one of the covariates did not meet the proportional assumption, so that the data re-modeled by using generalized Cox proportional hazard model called Cox extended model.
Although there are no differences among the explanatory variables that significantly affect the using of Cox proportional as Cox extended model, but the interpretation of both models is still different and based on the conducted test. The Cox extended model is the best model in modeling the birth data of the first child in Indonesia.
Acknowledgements
The first, authors would like to thankful to Allah SWT, my Parents (Syahruddin and Salmah K), lecturer, and my friends for support for this paper.