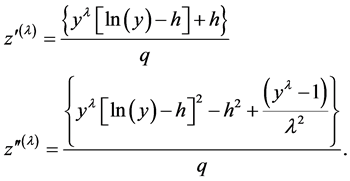Identifying Unusual Observations in Ridge Regression Linear Model Using Box-Cox Power Transformation Technique ()
Keywords: Box-Cox Transformation; Ridge Regression; Constant Variance Perturbation; Local Influence; Influential Observations
1. Introduction
Deletion diagnostics for assessing the influential cases on the power transformation parameter estimator in the Box-Cox linear unbiased regression model has been intensively studied in the last two and half decades (see [4-6]). Rather than deleting the influential case, [7] proposed a general method for assessing the local influence of minor perturbations of a statistical model. Lawrance [2] adapted Cook’s approach to obtain a diagnostic that can be used to examine the local changes of the transformation-parameter estimator caused by small perturbations on a constant-variance assumption. Tsai and Wu [8] analyzed the case-deletion model directly and obtain a more accurate and reliable transformation power estimator in weighted regression model. Also, Tsai and Wu [3] applied a case-weights perturbation scheme to obtain an alternative local influence diagnostic that takes into account the perturbation effects of the Jacobian.
In the literature, many authors noted that the influential observations on ridge type estimators are different from the corresponding least squares estimate (see [9]). The aim of this paper is to apply local influence of minor perturbation of constant variance to biased ridge regression Box-Cox power transformation model. The structure of this paper is as follows. Section 2 establishes transformation for ridge regression model for dealing with the local influence on the power transformation estimator. Section 3 gives calculation of the maximum local influence for ridge estimator. In Section 4 two real macroeconomic data sets are used to illustrate the methodologies. In the last section conclusions are given.
2. Transformation for Ridge Regression Model
A parametric family of transformations takes a column of a response vector y into
, where l is a scalar transformation parameter. It is assumed to be a value l0 of l, ensuring that 
follows a standard regression model, having the design matrix X. Thus, it is assumed that
(1)
where 
is ridge regression estimator (RRE) proposed by Hoerl and Kennard (see. [10,11]), X is a known full rank an 
matrix and 
an 
random error vector of RRE, it has a multivariate normal distribution with 
and 
here I is an identity matrix. The Equation (1) was originally proposed by Box-Cox [1]. If the Jacobian of the transformation denoted from 
to 
by
defined as 
and 
is the natural scaling of 
suggested by the likelihood.
Local Influence Approach for Power Transformation on RRE
For assessing the local influence on the power transformation estimator Lawrance [2] has obtained a diagnostic by perturbing the constant variance assumption.
First, here it is to be assumed that the variance of under perturbation is
(2)
where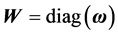 
is a diagonal matrix with diagonal elements of 
Let 
where w0 = 1, w denotes the an 
vector of case-weights for the regression, 
and 
is a fixed nonzero vector of unit length in Rq.
The distribution function for RRE linear model random error is
, (3)
where 
Jacobian of the transformation.
The perturbation of the distribution in Equation (3) becomes
(4)
The corresponding log-likelihood function for the untransformed observation y is
(5)
Thus the profile likelihood function for 
is obtained when maximizing RRE 
and 
for given data set y.
The maximum likelihood estimator (MLE) of 
is 
Also, the MLE of 
is 
this has to be estimated from the Equation (5) as
But,
where the 
is “hat” matrix of RRE. Therefore, the estimator of 
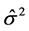is
From the above results the likelihood function for transformed observation y with perturbation can be written as
(6)
where 
is symmetric and 
The resulting MLE 
of 
can be found by minimizing Equation (6). Furthermore, the estimator 
can be regarded as a surface with Euclidean coordinates
. A curve over this surface is mapped from a straight-line path that passes through the point of the null perturbation. The direction and location of this path are specified by 
passing through the null point, where the quantity “a” measures distance along the line and 
are the direction cosines of Lawrance’s local influence diagnostic.
The partial differentiation of Equation (6) with respect to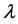 
is then the result will be arrived as,
But it is known that 
therefore, the above equation becomes
(7)
where 
is first derivative of 
The transpose of Equation (7) can be written as
(8)
The local influence diagnostic is the slope of the curve on the 
surface at the point of null perturbation, at 
If it is 0 small perturbations have no effect in the path points to the data cases being perturbed; the weighted set of cases that are most sensitive to local perturbations are thus specified by the direction that makes the path slope,
(9)
the greatest at the null point a = 0. This is the key idea in the local-influence approach. It is not principally the value of the slope, but the direction of maximum slope that is important and that forms the main diagnostic.
This description is the basis of Cook’s presentation when just one parameter is being considered; there is then no need to use a likelihood-displacement measure of the distance between 
and 
This also removes the need to consider curvature of the likelihood displacement, and avoids a loss of sign in connection with 
at a = 0.
3. Calculation of the Direction of Maximum Local Influence in RRE
In this section it is tried to develop a method which is the direction that maximizes the slope of 
at the origin of no perturbation is obtained.
Consider 
for a = 0 in an arbitrary direction 
Let W in Equation (2) have diagonal entries
and be denoted by 
for fixed 
denote 
with 
by
. Let L denote the diagonal matrix with diagonal entries
. The maximum likelihood estimator 
satisfies Equation (8) where each term is a function of
. Hence, differentiate the Equation (8) with respect to 
first differentiating with respect to 
when dealing with the variables 
and 
(10)
where 
is second order derivative of 
with respect to 
and can be called the second constructed variable; all 
terms in Equation (10) are used at 
Let consider
; where
.
Therefore, the perturbation matrix 
becomes
Now, partial differentiate 
with respect to 
then it gives
where
.
Let 
is a square matrix hence, the Equation (10) becomes
(11)
The direction 
of maximum slope is now determined by the Equation (11) and it gives the following results.
The matrix M can be written as
, where E and F are symmetric matrices. Therefore,
If the terms 
and 
denoted by 
and 
containing 
and
, respectively. Therefore, the Equation (11) becomes
(12)
Therefore, the direction of 
maximum slope is now easily determined from the Equation (12) that is 
where 
and yields the results for i-th 
is
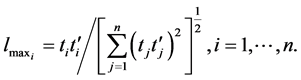(13)
Finally, consider the slope of 
at a = 0 when just the i-th variance is perturbed; denoting by
, gives
(14)
The result in Equation (14) is the local-influence version of computing 
after deleting the i-th data case, an operation analogous to the global perturbation 
and 
the global perturbation is itself algebraically intractable without approximation (see [5]).
4. Examples
4.1. Macroeconomic Impact of Foreign Direct Investment (MIFDI) in Sri Lanka Data Set
Sun [12] studied MIFDI in China 1979-1996. Based on his theory, the MIFDI data were collected in Sri Lanka form 1978 to 2004 to illustrate the methodologies derived in this paper. The data set consists four regressors (Foreign Direct Investment (FDI), Gross Domestic Product Per Capita (GDPPC), Exchange Rate (ER) and Interest Rate (IR)) and one response variable (Total Domestic Investment (TDI)) with 27 observations. The selected variables were tested for statistical conditions: 1) Cointegration, 2) Constant Error Variance and 3) Multicollinearity. The test results showed that: 1) Variables are cointegrated with a same cointegration coefficient I(1) at 1% level of significance, 2) The estimated Durbin-Watson value for the linear model is 2.0131 so, satisfied the constant error variance condition and 3) The scaled condition number of this data set is 31244, this large value suggests the presence of an unusually high level of multicollinearity among the regressors (the proposed cutoff is 30; see [9]). Hence, RRE is more preferable than ordinary least squares estimator to fit model for this data set.
The transformation parameter 
is estimated for this data set using the Box-Cox transformation model (necessary formulas for its implementations are given in the Appendix) is 
The 
after the scalepreserving transformation is 96.6%, the standard deviation 
is 1.23374, and there is hardly any interaction; these are considerable improvements over the original values of 95.9% and 12665.3 respectively, and a large interaction. The REE biasing parameter is estimated for this data set that is k = 0.0063. The lmax values are estimated using the Equation (13), the values and corresponding index plot are given in below Table 1 and Figure 1, respectively.
From Table 1 and Figure 1, it can be observed that the most five influential cases are 1, 3, 23, 14, and 20 in this order in the Box-Cox transformation analysis for RRE in MIFDI data.
4.2. Longley Data
The second data set is [13] to explain the influential observations on the Liu estimator. The scaled condition number of this data set is 43,275 (see [14]). This large value suggests the presence severe multicollinearity among regressors. Cook [15] used this data to identify the influential observations in ordinary least squares estimator using Cook’s Di and found that cases 5, 16, 4, 10, and 15 (in this order) were the most influential cases. Walker and Birch [14] analyzed the same data to detect anomalous cases in ridge regression using global influence method. They observed that cases 16, 10, 4, 15 and 5 (in this order) were most influential observations. Shi and Wang [16] also analyzed the same data to detect influential cases on the ridge regression estimator using
Table 1 . lmax in RRE using Box-Cox transformation.
local influence method. They detected that cases 10, 4, 15, 16, and 1 (in this order) were most anomalous observations. Researchers [17-22] also studied the same data to identify influential cases in modified ridge regression estimator and Liu estimator using global influence, local influence and Cook’s minor perturbation methods and they identified 16, 4, 1, 10 and 15 were the most influential cases but the order of magnitude is changed.
For the Longley data the parameter 
is estimated using Box-Cox transformation model (necessary formulas for its implementations are given in the Appendix) is
. The adjusted 
after the scale-preserving transformation is 99.3%, the standard deviation 
is 3.42981, and there is hardly any interaction; these are considerable improvements over the original values of 99.3% and 16.8976, respectively, and a large interaction. The RRE biasing parameter for Longley data is k = 0.00146. The lmax values are estimated using the Equation (13) and index plot for these values are given below.
From the index plot in Figure 2 it can be seen that the most five influential cases are 13, 10, 14, 8, and 12 in this order in the Box-Cox transformation analysis for RRE in Longley data. Compare the influential cases detected by this method and the previous studies, there are some new influential cases were detected.
Figure 1. Index plot of lmax in RRE using Box-Cox transformation in MIFDI data.
Figure 2. Index plot of lmax for RRE using Box-Cox transformation in longley data.
5. Conclusions
In this paper, I have studied Box-Cox power transformation for biased RRE that seem practical and can play a considerable part in RRE data analysis. The local influence measure introduced focus on perturbing the constant variance. The influential cases detected by this method for biased RRE are different than the influential cases detected in global and local influential method for RRE.
Although no conventional cut off points are introduced or developed for the RRE Box-Cox power transformation diagnostic quantities, it seems that index plot is an optimistic and conventional procedure to disclose influential cases. It is a bottleneck for cut off values for the influence method. Also, the issue of accommodating influential cases has not been studied. These are additional active issues for future research study.
[2] G. E. P. Box and D. R. Cox, “An Analysis of Transformation (with Discussion),” Journal of the Royal Statistical Society, Series-B, Vol. 26, 1964, pp. 211-252.
[3] A. J. Lawrance, “Regression Transformation Diagnostics Using Local Influence,” Journal of the American Statistical Association, Vol. 83, No. 404, 1988, pp. 1067-1072. http://dx.doi.org/10.1080/01621459.1988.10478702
[4] C. L. Tsai and X. Wu, “Transformation Model Diagnostics,” Technometrics, Vol. 34, No. 2, 1992, pp. 197-202. http://dx.doi.org/10.1080/00401706.1992.10484908
[5] A. C. Atkinson, “Plots, Transformations and Regression,” Oxford University Press, Oxford, 1985.
[6] R. D. Cook and P. C. Wang, “Transformations and Influential cases in Regression,” Technometrics, Vol. 25, No. 4, 1983, pp. 337-343. http://dx.doi.org/10.1080/00401706.1983.10487896
[7] D. V. Hinkley and S. Wang, “More about Transformations and Influential Cases in Regression,” Technometrics, Vol. 30, No. 4, 1988, pp. 435-440. http://dx.doi.org/10.1080/00401706.1988.10488439
[8] R. D. Cook, “Assessment of Local Influence,” Journal of Royal Statistical Association, Series-B, Vol. 48, 1986, pp. 133-169.
[9] C. L. Tsai and X. Wu, “Diagnostics in Transformation and Weighted Regression,” Technometrics, Vol. 32, No. 3, 1990, pp. 315-322. http://dx.doi.org/10.1080/00401706.1990.10484684
[10] D. A. Belsley, E. Kuh and R. E. Welsch, “Regression Diagnostics: Identifying Influential Data and Sources of Collinearity,” Wiley, New York, 1980. http://dx.doi.org/10.1002/0471725153
[11] A. E. Hoerl and R. W. Kennard, “Ridge Regression: Biased Estimation for Non-Orthogonal Problems,” Technometrics, Vol. 12, No. 1, 1970, pp. 55-67. http://dx.doi.org/10.1080/00401706.1970.10488634
[12] A. E. Hoerl and R. W. Kennard, “Ridge Regression: Application to Non-Orthogonal Problems,” Technometrics, Vol. 12, No. 1, 1970, pp. 69-82. http://dx.doi.org/10.1080/00401706.1970.10488635
[13] H. Sun, “Macroeconomic Impact of Direct Foreign Investment in China 1979-1996,” Blackwell Publishers Ltd., 1988.
[14] J. W. Longley, “An Appraisal of Least Squares Programs for Electronic Computer from the Point of View of the User,” Journal of American Statistical Association, Vol. 62, No. 319, 1967, pp. 819-841. http://dx.doi.org/10.1080/01621459.1967.10500896
[15] E. Walker and J. B. Birch, “Influence Measures in Ridge Regression,” Technometrics, Vol. 30, No. 2, 1988, pp. 221-227. http://dx.doi.org/10.1080/00401706.1988.10488370
[16] R. D. Cook, “Detection of Influential Observations in Linear Regression,” Technometrics, Vol. 19, No. 1, 1977, pp. 15-18. http://dx.doi.org/10.2307/1268249
[17] L. Shi and X. Wang, “Local Influence in Ridge Regression,” Computational Statistics & Data Analysis, Vol. 31, No. 3, 1999, pp. 341-353. http://dx.doi.org/10.1016/S0167-9473(99)00019-5
[18] A. Jahufer and J. Chen, “Assessing Global Influential Observations in Modified Ridge Regression,” Statistics and Probability Letters, Vol. 79, No. 4, 2009, pp. 513-518. http://dx.doi.org/10.1016/j.spl.2008.09.019
[19] A. Jahufer and J. Chen, “Identifying Local Influential Observations in Liu Estimator,” Journal of Metrika, Vol. 75, No. 3, 2012, pp. 425-438. http://dx.doi.org/10.1007/s00184-010-0334-4
[20] A. Jahufer and J. Chen, “Measuring Local Influential Observations in Modified Ridge Regression,” Journal of Data Science, Vol. 9, No. 3, 2011, pp. 359-372.
[21] A. Jahufer, “Detecting Global Influential Observations in Liu Regression Model,” Open Journal of Statistics, Vol. 3, No. 1, 2013, pp. 5-11. http://dx.doi.org/10.4236/ojs.2013.31002
[22] A. Jahufer and J. Chen, “Identifying Local Influence in Modified Ridge Regression Using Cook’s Method,” Sri Lankan Journal of Applied Statistics, Vol. 9, 2008, pp. 93-108.
[23] J. Chen and A. Jahufer, “Assessment of Anomalous Observations in Liu Estimator,” Journal of Management, Vol. 5, 2009, 41-49.
Appendix: Constructed Variables for the Box-Cox Power Family
A useful class of transformations is the power transformation
, where 
is a parameter to be determined. Box-Cox [1] showed how the parameters of the regression model and 
can be estimated simultaneously using the method of maximum likelihood estimation method.
The procedure based on the [2] consists of performing a standard least squares fit using
where 
and 
is the geometric mean of 
Writing 
and 
the two vectors of constructed variables required for variance perturbations are
