Comparative Evaluation of Elliptic Curve Cryptography Based Homomorphic Encryption Schemes for a Novel Secure Multiparty Computation ()
1. Introduction
Our handhelds have become smaller; computers faster; disks larger; networks more efficient and we enjoy bandwidths like never before; everything grew exponentially. All this sums up to a very favourable environment for data collection, transfer and storage. In order to fully utilize this data, there is a need to perform collaborative computation on data. However, the data collected mostly contain information related to individuals, their financial status, lifestyle and social behaviour in general. Joint computation on data may pose threat to privacy of individual’s data. Hence, there is a need to device a protocol that performs joint computation on private data without revealing data to other parties. Secure Multiparty Computation (SMC) addresses this issue. The general framework for SMC consists of specifying a random process that maps m inputs (local inputs of parties) to m outputs (desired outputs) [1]. The random process describes desired functionality. We focus on addition function in this paper.
There are many real world scenarios where privacy can be an issue, a few of which are worth mentioning. Consider the field of medical research. Consider the case that a number of different hospitals wish to perform joint research on their patient data. Also, let us assume that privacy policy and law prevent these hospitals from over pooling their data or revealing it to each other, due to the confidentiality of patient records. In such cases, it is necessary to find a solution that enables the hospitals to compute the desired functionality on the union of their databases, without ever pooling or revealing their data.
Consider the interaction between different intelligence agencies; for security purposes, these agencies cannot allow each other free access to their confidential information; if they did, then a single mole in a single agency would have access to an overwhelming number of sources. It is much more likely that suspicious behaviour would be detected if different agencies were able to perform computations on their combined data [2].
One way to compute the desired functionality is to use Trusted Third Party (TTP). In this scenario, parties send their data to TTP and TTP then computes results on parties’ data and sends the output to all parties. However, the pivotal question in cryptography is to achieve TTPs that are indeed trusted. This demands protocols that eliminate TTP. In this paper, we propose a protocol that eliminates TTP.
There are three approaches to performing desired functionality in Secure Multiparty Computation viz. the Oblivious Transfer [3] Protocol, the homomorphic encryption [4] and the secret sharing [5]. The oblivious transfer protocol is costly in terms of computational and communication overheads. The secret sharing based approach gives better results in terms of computational cost due to primitive operations involved [6]. However, it requires existence of private channels. In addition, as pointed out in [7], the communication cost is higher due to message exchange between other parties in the protocol as explained in Section 3. The homomorphic encryption based approach does not require existence of private channel and assures high level of privacy. Hence, we focus on homomorphic encryption based approach in this paper. The homomorphic encryption is introduced in Section 2.
In literature, there do exist approaches that perform secure multiparty computation using homomorphic encryption. However, they use classical encryption schemes [8,9]. Elliptic Curve Cryptography (ECC) based approach gives promising results as classical encryption schemes [10,11]. This is due to the higher per bit security provided by ECC. To give an example, to provide equivalent security of 1024-bit RSA, an ECC scheme needs 160 bits parameters [12]. Hence, in this paper, we utilize ECC based approach to implementing secure multiparty computation. The approach is described in Section 3. We investigate various additively homomorphic encryptions schemes and analyze them empirically in Section 4.
A few approaches utilize ECC based encryption schemes. However, they require multiple encryptiondecryption at each site and hence are computationally expensive [13,14]. In our approach, we avoid multiple cipher operation at each site and thus reduce the computational cost of SMC. We justify this in Section 3.
2. Background and Related Work
The multi-party computation problem was introduced by Yao [15] and extended by Goldreich, Micali and Wigderson [16]. The basic method they use is to represent the problem as combinatorial circuit. Participating parties then run a protocol for every gate in the circuit. Though general and simple, the approach exhibits combinatorial explosion in terms of circuit size and hence not scalable for large inputs. Apart from scrambled circuit, Goldreich [1] presents various other methods to perform multiparty computation such as homomorphic encryption and secret sharing. In literature, various applications such as Privacy Preserving Data Mining [17,18], Private statistical information retrieval [19,20], Privacy Preserving Database access [21] have been proposed that demand Secure Multiparty Computation among parties.
In Privacy Preserving Data Mining, various approaches for classification [22], clustering [23] and association rule mining have been proposed [24]. The basic building blocks in these approaches are private value addition and comparison. In this paper, we focus on private value addition. To give an example, in privacy preserving distributed clustering implements weighted average problem(WAP) as a basic building block [25]. Parties first perform local clustering at each site and then global cluster means are calculated using WAP. For example, consider two party scenario with party A and B. The sum of records and number of records for single cluster after computing local cluster means at party A and B is sumA, nA and sumB, nB respectively. Global means are computed using
. This requires the global addition of private value as a basic operation. Division is then carried out by parties locally [7].
In Wireless Sensor Network, the in-network processing demands the privacy. The in-network processing refers to on-the-fly processing of data packets by intermediate nodes before being communicated them to the base station. However, to protect the privacy of individual sensor reading, this on-the-fly processing must be done in a privacy preserving way. This process uses notion similar to multiparty computation. However, the computation is carried out at aggregator node only and not at all the nodes. This process utilizes homomorphic encryption schemes to be implemented at intermediate nodes.
2.1. Homomorphic Encryption
Homomorphic Encryption schemes allow parties to perform simple computations on encrypted data. As the computations are performed on encrypted data, the data is not revealed in the process and the privacy is preserved. Typically, a third party can calculate one of the encrypted sum or the encrypted product of two encrypted messages. This makes homomorphic cryptosystems useful in secure multiparty computation and a wide variety of privacy preserving protocols.
The additive homomorphic algorithm whose input is the public key of the encryption scheme and two ciphertexts, and whose output is 
; where 
is the homomorphic addition function,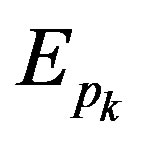 
is the publickey encryption function and 
and 
are elements in the domain of data. We refer additively homomorphic encryption scheme based on ECC in this paper.
2.2. Elliptic Curve Cryptography (ECC)
ECC is a public key cryptography approach based on the algebraic structure of elliptic curves over finite fields [10,11]. There are two types of finite fields where the elliptic curves are defined: prime fields Fp, where p is a large prime number, and binary fields
. In this work, we are interested in the use of elliptic curves over prime fields E (Fp). A nonsupersingular elliptic curve E over Fp is defined as the solution of 
to the cubic equation:
where a, 
such that 4a3 + 27b2 ≠ 0 (mod p) together with a special point ∞ called the point at infinity, The group of points forms an abelian group with addition operation so that the addition of any two points results in another point on the same curve. The security of ECC based cryptographic protocol is based on the Elliptic Curve Discrete Logarithm Problem (ECDLP). The ECDLP can be defined as the problem of finding the scalar k such that Q = kP given Q and P (generator point).
2.3. Algorithms Used for Evaluation
We utilize additively homomorphic encryption schemes for evaluation. We investigate four algorithms that are additively homomorphic. They are Elliptic Curve Naccache-Stern (EC-NS) Encryption [26], Elliptic Curve Okamoto-Uchiyama (EC-OU) Encryption [27], Elliptic Curve Paillier (EC-P) Encryption [28] and Elliptic Curve Elgamal(EC-EG) Encryption [29]. First three schemes are described in [30] and are Elliptic Curve variants of the previously proposed schemes by Naccache-Stern [26], Okamoto-Uchiyama [27] and Pailler [28]. EC-EG is the variant of ElGamal [29]. Original ElGamal is multiplicatively homomorphic while EC-EG is transformed to additive group and hence is additively homomorphic. The pseudo code and other details may be found in [30].
3. The Proposed Approach: Secure Multiparty Computation Using ECC
We propose novel approach to Secure Multiparty Addition problem using ECC. Secure Multiparty Addition have beem implemented for privacy preserving data mining using homomorphic encryption [25] and secret sharing [7]. However, the approach of [25] uses classical public key encryption scheme and hence is computationally expensive. Further, multiple cipher operations at each site increased the computational cost. The secret sharing based approach proposed in [7] is efficient in terms of computational cost. However, due to two rounds of information exchange among parties increases the communication cost. Among the three approaches to implement SMC viz. the oblivious transfer based, the homomorphic encryption based and the secret sharing based, we focus on homomorphic encryption based approach.
We allow parties to communicate in ring topology. Consider three party scenario with parties A, B and C with private values m1, m2 and m3 respectively. Parties need to compute m1+ m2 + m3 securely. One party in the protocol is randomly designated as the Initiator party. The proposed approach considering party A as the Initiator is shown in Figure 1.
As shown in Figure 1, the initiator first encrypts its private value using ECC based encryption scheme. The resultant ciphertext (which is in the form of elliptic curve point) is sent to next party in the ring. Next party does not perform any cipher operation but just adds its own private value (mapped to elliptic curve point) with the received cipher text. This process is repeated and finally initiator receives the message E(m1) + m2 + m3 at the end of phase I. In phase II, initiator decrypts the message by removing the noise (that was added during encryption) from the message and computes m1+ m2 + m3. Here, initiator just removes the noise in order to get desired sum. Hence, we have slightly modified the decryption processes of algorithms to get the sum value. This sum is then sent to next party in the ring and eventually all parties will receive the sum.
4. Theoretical Analysis
In this section, we discuss the computational and communication cost of our proposed approach.
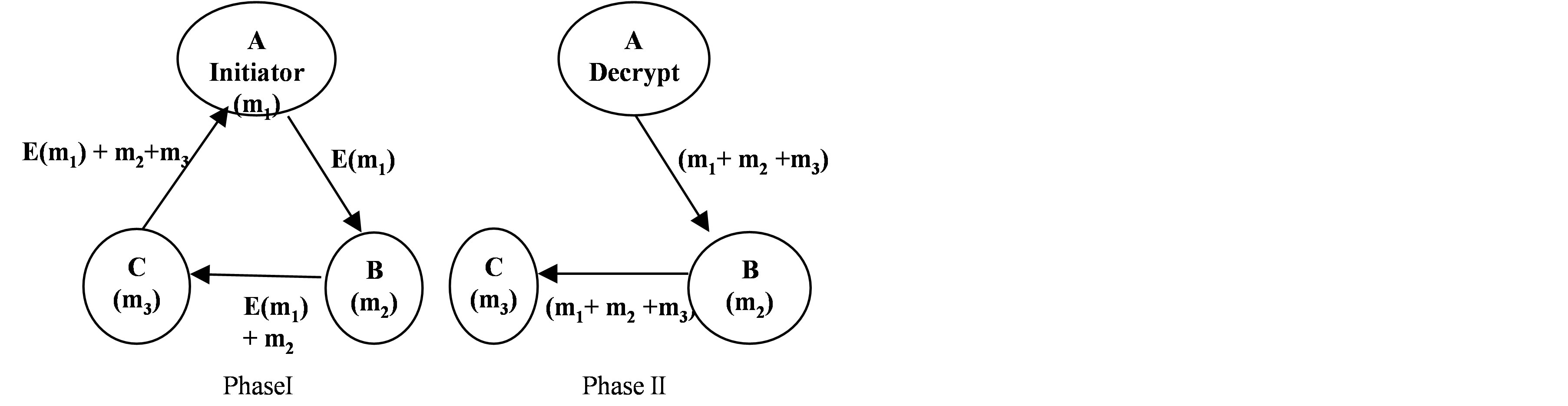
Figure 1. Secure Multiparty Addition using Elliptic Curve Cryptography.
4.1. Computational Cost
The computational cost is mainly due to the operations in first phase where parties send data to the next party in ring. However, we need to consider the cost for initiator and the rest of the parties separately. This is because the initiator encrypts and decrypts the data and the rest of the parties just need to add their data in the received data. Suppose to encrypt the data, time taken is T1. It is pointed out in [10] that by means of O(logk) addition and doubling, one can compute k. M value. Hence, T1 becomes O(logk). Further, to decrypt the data, time taken is T2. Let us have the time taken by other parties to add their data point is T3. Hence, the computation cost for initiator can be = (O(logk) + T2) = O(logk). For the rest of the parties the cost becomes T3 and hence O(1). For total of N parties the cost becomes O(logk) + O(N).
4.2. Communication Cost
Our proposed approach involves two phases. In first phase, single message (as elliptic curve points) is communicated by each party to the next party in the ring. Hence, total N messages are transmitted for N party scenario. In second phase, only the sum (that is calculated) by initiator party is communicated to all parties in a ring. The last party in the ring need not send this sum to initiator. Hence, total (N-1) messages are transmitted in second round. Thus for N parties in the protocol, the communication cost becomes O(N) i.e. linear in terms of number of parties.
4.3. Comparison with Secret Sharing Based Approach
Our proposed approach is closest to the approach of [7]. In [7], privacy preserving clustering protocol is proposed using secret sharing scheme. The basic building block they use is the secure multiparty addition. Hence, we compare our approach with the approach of [7]. The approach of [7] is efficient in terms of computational cost due to primitive operations required in secret sharing scheme. However, approach of [7] requires message exchange among every other party in the protocol. Table 1 shows the comparison in communication cost. We achieve O(N) complexity with respect to communication cost as compared to O(N2) of secret sharing based approach. Hence, our approach achieves scalability with respect to number of parties in the distributed scenario.
Table 1. Comparison with respect to communication cost between our approach and approach of [7].
5. Experimental Results
In this paper, we focus on comparative evaluation of ECC based homomorphic encryption schemes to implement secure multiparty addition. We implement our proposed secure multi party addition protocol using four ECC based schemes such as EC-NS, EC-OU, EC-P and EC-EG.
5.1. Experimental Setup
We carry out the experiments in JAVA. The experiments are conducted on three different machines to emulate the true distributed scenario consisting of three parties. All machines have similar configuration of Intel Core i5 processor, 4GB of RAM and 3.20 GHz of processing power. All reported results are averaged from 5 runs of the protocol.
All the participating parties initially agree upon the ECC parameters required for the respective ECC algorithm. The ring topology among the parties is set up and each party knows its neighbor on ring. One party in a ring is randomly designated as Initiator.
The secure three party addition protocol is implemented with four different homomorphic algorithms based on ECC. Our test application successfully shows fully functional secure three party addition protocol over real network.
5.2. Experimental Results
We evaluate ECC based encryption schemes for secure multiparty addition based on two metrics viz. the computational cost and the communication cost. Computational cost is measured as time taken for computation and communication cost is measured as number of bytes exchanged over communication channel.
We perform experiments with different ECC parameter sizes viz. 112-bit, 160-bit and 256-bit. For EC-OU, the prime value is 341 bit long and for remaining encryption schemes, prime value is similar to the size of Elliptic Curve Parameter Size i.e. 112 bit or 160 bit or 256 bit.
Table 2 shows the cost for running secure three party addition protocol using four ECC based encryption schemes.
As shown in Table 2, EC-EG gives better performance among all in terms of computational cost. However, if we consider the communication cost, EC-OU gives better performance. The result for higher computational cost for EC-OU is that in EC-OU, prime number p,q are 341 bits long and for other schemes prime numbers are same as the size of EC parameter size. To get the fair comparison, we then took random parameter size as 341 bits for all the algorithms and measure the cost of running secure multiparty addition using 341-bit value. The results are shown in Table 3.
Table 2. Results for Secure Multiparty Addition using various ECC based encryption schemes.
Table 3. Results for Secure Multiparty Addition using various ECC based encryption schemes keeping 341-bit primes for all schemes.
Table 3 shows that keeping 341-bit prime value fixed for all schemes results in higher computational cost for the encryption schemes other than EC-OU. In these experiments, we found that EC-OU and EC-EG takes lesser time where as EC-OU takes lesser space which is reasonably lesser than the other three schemes. Results for computational and communication cost are shown in Figures 2 and 3 respectively for varying length of primes.
Results for computational and communication cost for 341-bit fixed length prime are shown in Figures 4 and 5 respectively. As shown in Figures 4 and 5, if we consider both computational and communication cost, EC-OU perform better than all algorithms selected for evaluation.
6. Conclusion
In this paper, we propose a novel approach to securing multiparty computation using elliptic curve cryptography. We empirically evaluated various ECC based homomorphic encryption schemes for our proposed protocol. We demonstrate that EC-OU algorithm performs better among four selected algorithms. Our secure multiparty addition protocol achieves better efficiency in terms of communication cost as compared to corresponding secret sharing based approach and hence is scalable with respect to a number of parties. In addition, we highlighted various applications such as privacy preserving data mining as the candidate applications for our proposed approaches.
Figure 2. Comparison of Computatio nal cost for various ECC schemes for varying length of prime.
Figure 3. Comparison of Communication cost for various ECC schemes for varying length of prime.
Figure 4. Comparison of Computational cost for various ECC schemes for 341-bit prime.
Figure 5. Comparison of Communication cost for various ECC schemes for 341-bit prime.
Our future includes incorporating EC-OU based secure multiparty computation in privacy preserving data mining application.