High-Dimensional Regression on Sparse Grids Applied to Pricing Moving Window Asian Options ()
1. Introduction
Methods for pricing a large variety of exotic options have been developed in the past decades. Still, the pricing of high dimensional American-style moving average options remains a challenging task. The price of this type of options depends on the full path of the underlying, not only at the final exercise date but also during the whole period of exercisable times. We consider in this paper the case of an early-exercisable floating-strike moving window Asian option (MWAO) with discrete observations for the computation of the exercise value. The exercise value of the MWAO depends on a moving average of the underlying stock over a period of time.
Carriere [1] first introduces the simulation-based method for solving American-type option valuation problems. A similar but simpler method is presented by Longstaff and Schwartz [2]. Their method is known as the Least Squares Monte Carlo (LSM) method. It uses the least-squares regression method to determine the optimal exercise strategy. Longstaff and Schwartz also use their LSM method to price an American-Bermuda-Asian option that can be exercised on a specific set of dates after an initial lockout period. Their American-Bermuda-Asian option has an arithmetic average of stock prices as the underlying. The pricing problem can be reduced to two dimensions after introducing another variable in the partial differential equation (PDE) to represent the arithmetic average.
The dimension reduction technique as in LongstaffSchwartz [2] can not be applied for the pricing problem of MWAOs. Since moving averages shift up and down when the underlying prices shift up and down especially when the first observation in the moving window drops out and a new one comes in, the whole history of stock prices is important in determining the optimal exercise strategy of MWAOs. This leads to an arbitrary number of dimensions and presents a computational challenge. Pricing methods for MWAOs have been described by very few authors besides Broadie and Cao [3]. Broadie and Cao price a fixed strike MWAO, using polynomials of underlying asset price and arithmetic average as the regression basis function. Bilger [4] applies the LSM method to price MWAOs. He uses a different choice of basis functions (i.e. the underlying asset S and a set of averages) for evaluating the conditional expected option value. Kao and Lyuu [5] present results for moving average-type options traded in the Taiwan market. Their method is based on the binomial tree model and they include up to 6 discrete observations in the averaging period for their numerical examples. Bernhart et al. [6] use a truncated Laguerre series expansion to reduce the infinite dimensional dynamics of a moving average process to a finite dimensional approximation and then apply the LSM algorithm to price the finite-dimensioned moving average American-type options. Their numerical implementations can handle dimensions up to 8, beyond that their method becomes infeasible. Dai et al. [7] use a forward shooting grid method to price European and American-style moving average barrier options. The window lengths in their numerical examples range from three or four days to two or three months.
In this paper, we apply an alternative type of basis functions—the sparse grid basis functions—to the simulation-based LSM approach for pricing American-style MWAOs. The sparse grid technique overcomes the low-dimension limit associated with full grid discretizations and achieves reasonable accuracy for approximating high-dimensional problems. Instead of using a predetermined set of basis functions in the least squares regressions, the sparse grid basis functions are adaptive to the data—it is more general and considers as many information in the moving window as possible. Using numerical examples, we demonstrate the convergence of the pricing algorithms for MWAOs for different numbers of Monte-Carlo paths, different sparse grid levels and a fixed length of observation period of 10 days. Sparse grid is a discretization technique that is designed to circumvent the “curse of dimensionality” problem in standard grid-based methods for approximating a function. The idea of sparse grid was originally discovered by Smolyak [8] and was rediscovered by Zenger [9] for PDE solutions in 1990. Since then, it has been applied to many different topics, such as integration [10,11] or Fast Fourier Transform (FFT) [12]. Sparse grids have also been used for finite element PDE solutions by Bungartz [13], interpolation by Bathelmann et al. [14], clustering by Garcke et al. [15], and PDE option pricing by Reisinger [16].
The structure of this paper is as follows: first, we formulate the pricing problem of a moving window Asian option and explain why this problem is computationally challenging. This is followed by a brief description of the LSM approach and the sparse grid technique. Finally, we provide some numerical examples for pricing MWAOs with discretely sampled observations using LSM with sparse grid type basis functions.
Throughout this paper, we consider equity options on a single underlying stock in the Black Scholes [17] framework.
2. Moving Window Asian Option
MWAO is an American-style option that makes use of the moving average dynamics of stock prices. Similar to an American option which pays the difference between the current underlying price and a fixed strike, a MWAO pays the difference between current stock price and the floating moving average or the difference between a floating moving average and a fixed strike.
2.1. Continuous Time Version
Before going into the details of an MWAO, we set up the process for the underlying stock. The stock prices are assumed following a geometric Brownian motion (GBM) process
(1)
where 
is the constant riskless interest rate, 
is the constant stock return volatility and 
is the increment of a standard Wiener process under the risk-neutral measure. The initial stock price is denoted as 
and at time 
the stock price is
. The value of a MWAO option written on the stock is denoted in general as
, or 
resp. 
when we stress the dependence on 
or
. The option value 
satisfies the following Black Scholes PDE
(2)
The following American constraint sets a minimum value for the function
. The constraint has to be satisfied at each time
, where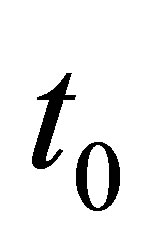 
denotes the setup time of the option and 
denotes a fixed window length
(3)
(4)
where 
is the payoff of a MWAO from exercise at time
. It depends on the stock price 
and a weighted moving average 
of the stock prices. The moving average 
is computed using the weight function 
on a window of stock prices ranging from time 
to time
. In this paper, we consider the payoff function
(5)
when setting the weight 
in (4), we have an equally-weighted arithmetic moving average
Differentiating this expression with respect to time 
leads to
where the updating process of 
depends not only on the stock price at time
, but also on the stock price at time
. This is clearly not Markovian. An optimal exercise strategy performed on the above moving average process 
has to consider
, 
and all stock prices 
in between. Since all the values 
are used in computing the moving average
, and 
in turn determines the MWAO payoff in (3), there are infinitely many prices involved in the computation of an optimal exercise strategy. This is a challenging infinite-dimensional problem in continuous time [6,7].
2.2. Discretizations
To implement the pricing problem for the MWAO, we consider the finite dimensional case with discretely sampled observations. Define a set of times
with
, and 
for
. At time
, the value of 
and 
is respectively denoted as 
and
.
We consider constant weight 
in defining a discretely sampled moving average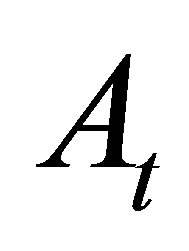 
(6)
where 
denotes the number of samples used in computing the moving average. Using the weight function 
in defining the moving average
, the boundary condition (3) at times 
has the following discretized form
(7)
where the weight function 
assigns a zero weight to an initial observation in the moving window and a weight of one to the rest of the observations. With this weight function we have effectively used the past 
samples to form the moving window. The above condition holds for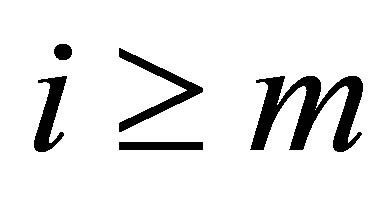
, after an initial allowance for the window length. The dimension of this MWAO problem equals to the number of discrete samples 
used in the averaging window.
Our method for valuing the MWAO uses the discretized process and a quadrature of
. The valuation proceeds backwards in time, starting at the option maturity
, where condition (7) holds with equality. Then we solve for the option value at current time
. For short window length 
and thus low dimensionality, this procedure can be reformulated in a PDE setting and solved numerically. However, due to the “curse of dimensionality”, the PDE method is ineffective for dimensions of more than three or four. For window length 
larger than four, the high dimensional problem has to be solved using approximate representations or special numerical techniques.
3. Numerical Procedure
The previous sections provided the mathematical formulations and discussed the discretization issues related to the MWAO. This section details the numerical methods we use for pricing MWAOs. The algorithm proposed by this paper is effectively a combination of three techniques that are well established in their respective fields. The three techniques that we use as a practical tool for valuing a MWAO are Monte Carlo simulation, least squares regression and sparse grids. Especially in quantitative finance, sparse grids technique has not yet lived to its full potential. This paper contributes to use sparse grids in solving high-dimensional problems. Since all the three techniques have been documented in full detail by the cited sources, we summarize in the following the main aspects of each technique. Without explicitly mentioning it, all prices in our computations are discounted prices, meaning that prices are already normalized by the bank account numeraire. We use
, 
and 
to denote discounted stock prices, discounted payoffs and discounted option values.
3.1. Monte Carlo Simulation
A standard method that is used when dimensionality causes numerical difficulties is the Monte Carlo simulation method. This method alone does not resolve our issue, but provides the framework for our algorithm. We assume that the stock price underlying a MWAO follows the GBM process defined in (1). The discretized stock price process is sampled at the set of discrete times 
so that each of the realizations
, 
with 
denoting the number of Monte-Carlo paths, has the following normalized representation
(8)
where 
is drawn from a standardized Normal distribution.
The price of the MWAO is the expected value of the (discounted) payoff at the optimal stopping time. The optimal stopping time provides a strategy that maximizes the option value without using any information about future stock prices.
3.2. Least Squares
At each exercise time
, the option holder decides whether to exercise the option and get the payoff 
or to continue holding the option. In order to maximize the option value 
at time
, the holder exercises if
(9)
where 
denotes the expectation taken under the risk neutral measure. In the LSM approach, the value of 
is approximated by a function 
(10)
The value of 
is computed using a least square regression on many path-realizations
. The regressions start at one time step before the maturity
.
The function 
is a linear combination of the basis functions 
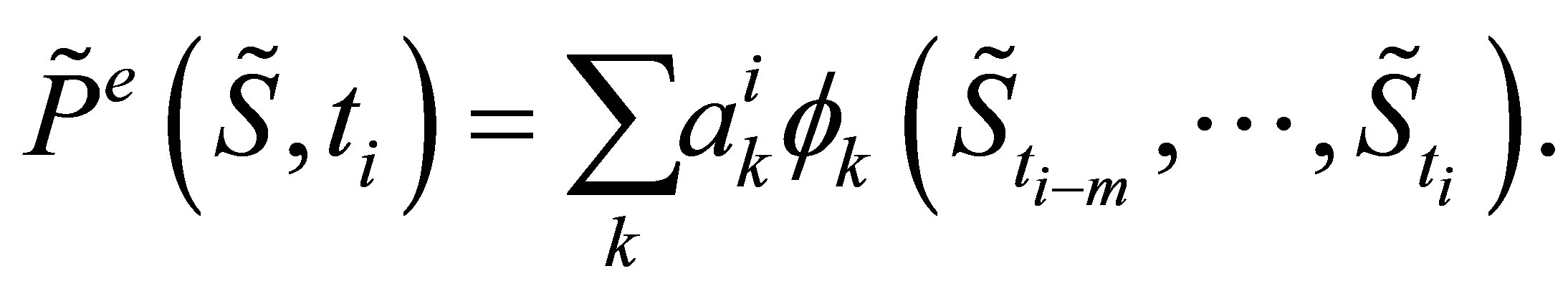(11)
The coefficients 
are found by minimizing the 
-norm
(12)
where 
is the option value of a Monte Carlo path realization 
at time
. The option value 
is given as the maximum between the estimated continuation value and the intrinsic value. A numerically more stable algorithm is to set
(13)
where the computed 
is used only in earlyexercise decisions, this avoids the accumulation of approximation errors when stepping backwards in time.
Given the option payoff 
at maturity time, a backward induction dynamic programming method solves for all values
, starting at time 
and iterating back to
. Based on the values
, we compute an estimated option value, known as the in-sample price
(14)
This approach has an obvious shortcoming. Each of the estimated option values 
contains information about its future stock path
. In order to avoid this perfect foresight bias, we compute an out-of-sample option price: we generate additional simulation paths
, 
but use the coefficients 
fitted to the old set of simulation paths
,
. Consequently, the out-of-sample value does not depend on knowledge of the future paths. The out-of-sample option value is computed by
(15)
with
(16)
In our implementations, we compute only the out-ofsample value since it is the value for which we can state the optimal exercise policy without information about the future. The expected value of the out-of-sample price 
is always a lower bound for the option value, and the estimate 
is crucial for the convergence of the least squares Monte Carlo simulation method. We are confined to finitely many samples and to finite degrees of freedom in the regressions, thus are not able to perfectly represent the real shape of 
using the estimate
. A less than optimal exercise strategy is performed and provides a lower biased option value.
3.3. Basis Functions
An important issue in the LSM approach is a careful choice of the basis functions 
in (11). We will use in this paper a linear combination of the sparse grid type basis functions to approximate the conditional expected value 
involved in the optimal exercise rules. We need one dimension for each observation in the averaging window, this leads to a high dimensionality in the computational problem. Sparse grid [8] is a discretization technique designed to circumvent this “curse of dimensionality” problem. It gives a more efficient selection of basis functions. This technique has been successfully applied in the field of high-dimensional function approximations [15] and many others [10,13,16,18].
In the following we provide a brief description of the sparse grid approach. We start from constructing onedimensional basis functions in a general case and show how to build multi-dimensional basis functions from the one-dimensional ones. Next we create a finite set of basis functions for numerical computations. Sparse grid then efficiently combines the sets of basis functions in a way such that the resulting function set is linearly independent. Following this, we detail on two specific types of sparse basis functions - a polynomial function and a piecewise linear function - to be used as the basis functions in the LSM regressions in this paper.
3.3.1. Constructing the Basis Functions
When approximating a function with simpler functions or numerically extracting the shape of a function, it is common to build such a function representation using some basis functions. We consider here a set of basis functions 
and we call the set (sets) of basis functions “function basis (bases)”. From the set
, we construct an approximating function 
as a linear combination of the basis functions
(17)
with coefficients 
for
, and 
for some set
. The basis functions 
can be a one-dimensional or multi-dimensional mapping from 
to
.
For the one-dimensional case, many function bases are well known and widely used. Examples include polynomials, splines, B-splines, Bessel functions, trigonometric functions, and so on. For the multi-dimensional case, the set of basis functions that are commonly used is more scarce. There are two common approaches to constructing multi-dimensional basis functions from the one-dimensional ones: the radial basis functions [19] and the tensor product functions [20]. In this paper we focus on the tensor product approach. To construct a tensor product basis function, we select one-dimensional functions 
and multiply their respective function value evaluated at the corresponding component of
. Specifically, for 
and each m-dimensional basis function
, we choose a set of one dimensional functions
and
then multiply the 
-th function 
evaluated at the 
-th element
, for
, to have the following representation of an 
-dimensional basis function
(18)
3.3.2. Creating a Function Basis
Having created multi-dimensional basis functions in a general case, we now select a finite set of these functions to be our basis for numerical analyses. Since we will do computations on different levels of accuracy, we will also need a set of basis functions on different levels. Naturally, the more basis functions we put in the set, the more accurate are our function approximations.
We decide that on a level 
there are 
basis functions. The one-dimensional function basis 
with 
functions is the following set
(19)
where 
are one-dimensional basis functions, and 
is a monotonously increasing function that determines the size of our basis at level
.
In order to create an 
-dimensional function basis, we choose a level
. For each dimension
, the level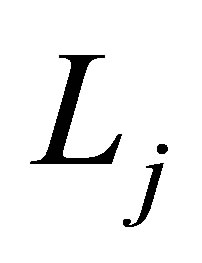 
implies a function basis 
via (19). Using the tensor product function, the 
-dimensional function basis 
is constructed as
(20)
where 
denotes any of the one-dimensional basis functions from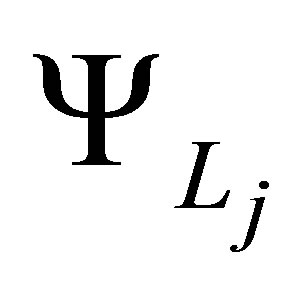
, evaluated at the 
th element of
.
It was our original goal to construct a function basis with increasing expressiveness for increasing levels. This multi-dimensional level 
is not a very good starting point. Consider the case where all dimensions are equally important, we would have to use a level of the form
. The size of the resulting function set would be extremely large, a phenomenon known as the “curse of dimensionality” problem:
(21)
Choosing 
dimensions and 
results in 
functions with a corresponding number of coefficients to be solved.
3.3.3. Sparse Grids
Sparse grids were developed as an escape from the “curse of dimensionality” problem. They allow reasonably accurate approximations in high dimensions at low computational cost. The idea behind the sparse grid is to combine the tensor basis of different levels.
Let 
be the set of basis functions on level
. We define it as the union of all tensor function bases 
where the sum of 
levels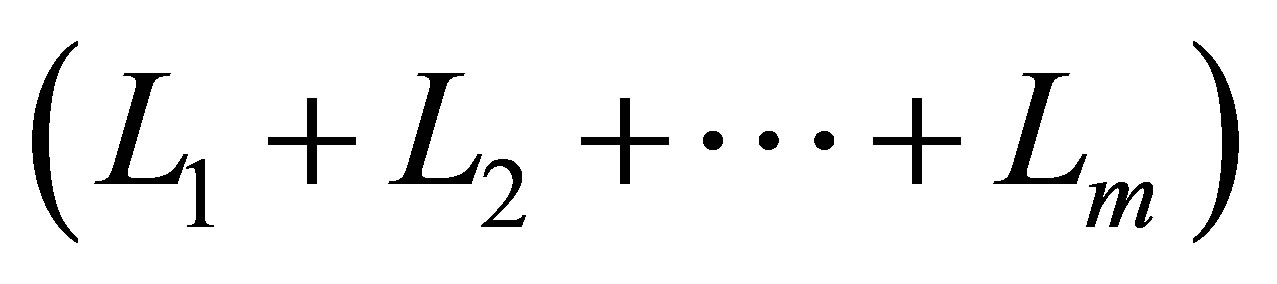 
is equal to
, with 
and 
denoting the set of all non-negative numbers
(22)
Considering a simple example with 
dimensions on level
, i.e.
. For 
with
, there are three possible combinations of the levels 
and 
that sum to 2:
, 
and
. From this, we could create a set 
as the union of the tensor function bases:
.
The first set 
has high resolution in the first dimension
, while the last set 
mainly resolves the second dimension
. By construction, basis functions with high resolution in both dimensions, such as
, are left out in the sparse set, making the sparse basis ideal for approximating functions with bounded mixed derivatives.
The computational effort of sparse grids compared with conventional full grids decreases radically while the error rises only slightly: for the representation of a function 
over an m-dimensional domain with minimal mesh size
, a sparse grid employs 
points and a full grid has 
grid points. At the same time, the 
interpolation error for smooth functions is 
for sparse grids and 
for full grids.
Having constructed a sparse basis 
on a top level, we now create two specific types of sparse basis functions that will be used as the function sets in our LSM regression problem: a polynomial sparse function basis and a piecewise linear function basis. Compared to the piecewise linear basis functions, the polynomial sparse basis functions are easier to understand and easier to implement. As solutions to higher dimensional problems, the piecewise linear basis functions are more adaptive. They can be extended to effectively place the basis functions on the dimension that contributes more to the problem solution. As a result, piecewise linear basis functions have seen wide applicability to solving PDEs [18] and interpolating functions [21]. In our paper, we use these two types of sparse basis functions to cross validate the results of our high dimensional pricing problem.
3.3.4. A Polynomial Sparse Basis
A polynomial function basis with 
basis functions in the one-dimensional case has the following construction
(23)
From the one-dimensional functions
, we can build a multi-dimensional tensor basis according to (20).
As an example, for the two-dimensional case
, we have the first dimension in 
with one-dimensional functions
and the second dimension in 
with one-dimensional functions
.
Equation (20) then gives the following list of tensor basis functions
(24)
Building upon the two-dimensional function basis
, we construct a sparse basis function set for the three sparse levels
, 
, and
, where
. We let the three levels correspond to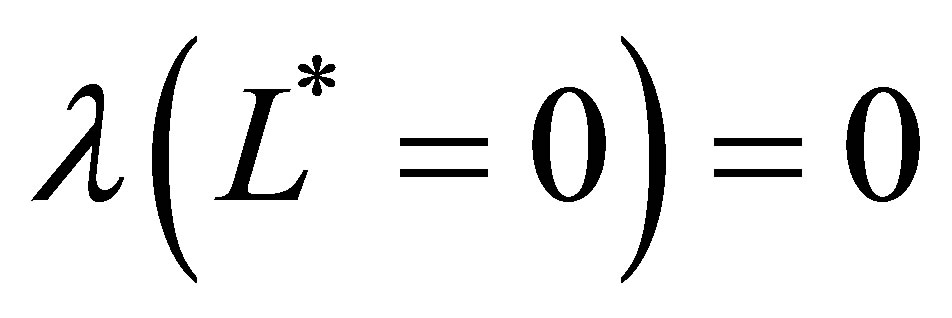
, 
and 
number of basis functions. Using (22) to unite the function sets, our sparse bases for the two dimensional function space are the following sets
(25)
The above sparse basis function sets 
are created by taking the unions of the tensor bases of 
according to (22). As an example, the sparse set 
is constructed as a union of
and
.
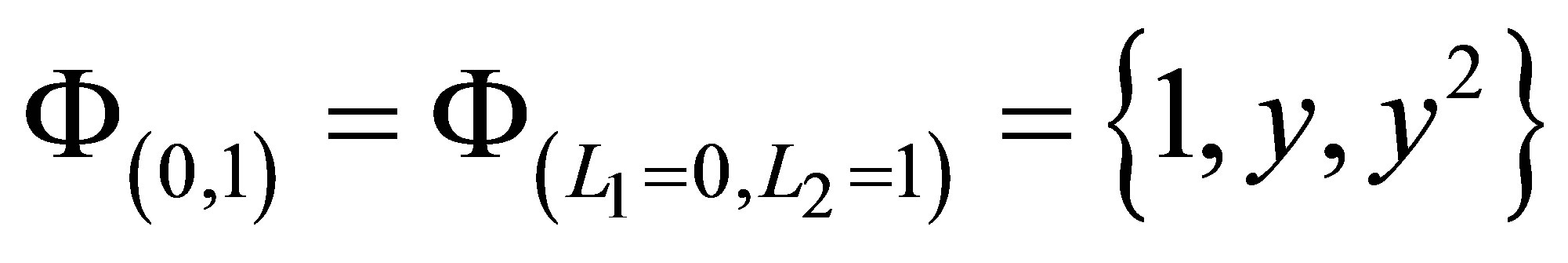The set 
is arrived at by having 
number of basis functions in the 
direction and 
basis functions in the 
direction from the two-dimensional set
, ceteris paribus.
We have just created a polynomial sparse basis 
in two dimensions. Higher dimensional function bases can be similarly constructed using the tensor product approach, depending on the dimension of the problem we intend to solve. In our LSM regression problems, we have for example used 
dimensions and a polynomial sparse level of
.
While the polynomial sparse basis functions aim for a global fit, the piecewise linear basis functions fit locally to the approximated functions and it is to the task of constructing the piecewise linear basis functions that we now turn.
3.3.5. Piecewise Linear Functions on [0,1]
The piecewise linear function is a type of basis function that is commonly used in sparse grid applications. To create a piecewise basis for various levels, we utilize a construction approach known from multi-resolution analysis. We define a mother function 
and generate our basis by scaling and translating from 
(26)
It has been found computationally advisable to have only one basis function on the first level. Hence we start with the constant 1 on level 
and transform 
on successive levels. This construction avoids the inclusion of costly boundary points by creating boundary functions that are less scaled than inner functions. Klimke and Wohlmuth [21] is a good reference on piecewise linear basis functions.
The one-dimensional function bases of levels
, 
, 
, 
, 
in 
as generated from the one-dimensional basis functions 
in (26) are the following sets
(27)
(28)
where the series 
in (28) is a sequence of odd numbers. The one-dimensional function bases in 
can be analogously generated from (26).
The construction of a two-dimensional sparse basis in the 
and 
directions respectively for levels
, L* = 1 and
, where
, follows from (22)
(29)
As an example, the sparse basis function set 
is created by taking the unions of the function bases of
, 
, and
, where 
is the tensor product of 
and
, with 
given in (27) and
. The set 
is constructed using the tensor product function (20).
The two-dimensional sparse bases can be extended to higher dimensions depending on the problem dimensions we intend to solve. The resulting higher-dimensional function sets can then be used in the LSM regressions by selecting an optimal sparse level for that problem dimension.
3.3.6. Implementations
We perform the regressions required by (12) on sparse polynomial basis functions 
and sparse piecewise linear basis functions 
as explained in Section 3.3.4 and 3.3.5, respectively. As an example, in the case of sparse polynomial basis functions of 
dimensions, the approximating function 
of (11) is a linear combination of the basis functions in the polynomial sparse basis set 
in (25). At sparse level
the set
, and the approximating function
For the sparse piecewise linear basis functions of 
dimensions, the approximating function 
is a linear combination of the basis functions in the piecewise linear sparse basis set 
in (29). At sparse level
, the set
and the approximating function
In our implementations, we use sparse levels 
from 
up to 
and dimensions 
for computing the basis functions. This is sufficient for our purposes. But, we do not perform the regressions on 
directly. Instead, we use scaled values of 
such that for each path
, we compute
where 
are defined such that
. For discretely sampled observations, the dimension of the problem is effectively 
dimensions because of the weight function 
used in computing the moving averages. When extrapolating to the continuous case, the dimension of the problem approaches infinity as 
goes to
.
The regression itself is performed solving the least squares problem of (12) via QR-decomposition. Furthermore, the regression is only performed on paths with a positive exercise value
. This significantly decreases the computational effort.
4. Numerical Example
We provide in this section a numerical case study of using sparse grid basis functions in LSM pricing MWAOs. We will use a discretely sampled averaging window spanning ten observations with the weight function α in (6).
The properties of the MWAO are defined in Table 1. The underlying stock prices are sampled at a regular frequency, e.g. every trading day at a specific time.
To analyze the convergence of our pricing algorithm for MWAOs, we use the notation 
to denote the out-of-sample result 
as defined in (15). Each Monte Carlo value 
depends on the number of sample paths
, the level of the sparse grid function basis
, the number of observations in the averaging window
, and the quadrature scheme
.
We compute different 
with
, 
, 
and 
fixed in order to get an estimate for the mean
(30)
of 
different Monte Carlo prices. Each 
valuation 
is based on a randomly generated
Table 1. Specifications of a moving window Asian option with a floating strike. The moving averages are based on discretely sampled stock prices.
Monte Carlo seed. The number of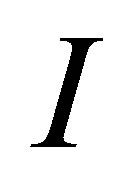 
ranges from 10 to 1000 depending on an estimate of the Monte Carlo error. For instance, if the error is acceptable based on our 95% confidence level at
, we stop the computation and obtain the mean price estimate using (30). Otherwise, we continue computing 
by increasing the value of 
until the error is acceptable. The number of samples 
per Monte Carlo price results from combining the in-sample paths 
and the out-of-sample paths 
such that
. We use 30% of the sample paths for regressions and 70% for option valuation out-of-sample.
Figure 1 presents the mean 
for different numbers of samples 
and different levels
, but with the dimensions 
and the weights 
fixed. Included in the figure are the results from the polynomial and the piecewise linear sparse basis functions. The option values at sparse level 
converge quickly to a value of about 
which does not change after 30,000 simulations. With
, the sparse level 
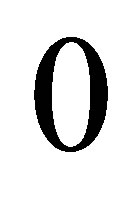consists of just one basis function (i.e. a constant) and the resulting exercising decision is almost trivial. Sparse level 
consists of 21 basis functions. This allows for a more sophisticated strategy with a better utilization of the option. After about 300,000 simulations, the option value saturates at 7.62 for both polynomial and piecewise linear basis functions. The sparse level 
with 241 basis functions results in similar values after 1,000,000 simulations. For the polynomial sparse basis functions, a third level 
with 2001 basis functions already exceeds our available computational resources, such that the saturation level could not be computed. The values for polynomial sparse level 3 are thus not presented. One
Figure 1. The option values for MWAO. The figure shows MWAO values estimated by least squares Monte Carlo combined respectively with polynomial sparse basis functions and with piecewise linear sparse basis functions. The sparse level ranges from 0 to 3 and the number of simulation paths runs from 
to
. In the figure, “polynomial basis level #” refers to the MWAO values estimated with the polynomial basis functions at a sparse level #, where # is the number for the sparse level. Similarly, “piecewise basis level #” points to MWAO values estimated with the piecewise linear basis functions at the sparse level #. The data for the MWAO are specified in Table 1.
thing worth mentioning is that higher sparse levels initially perform inferior to lower sparse levels due to the over-fitted regression functions.
The corresponding values in Figure 1 are presented in Table 2 for polynomial sparse basis functions and in Table 3 for piecewise linear sparse basis functions. The mean values of a series of valuations
,
, is denoted by 
(30), the standard deviation of the series across 
valuations is denoted by
. For a single evaluation 
with LSM, 
can be seen as a measure of how close the value is to the mean of 
valuations. Thus 
does not measure the error relative to the true option value. The mean estimate 
(30) will be biased lower than the true values due to the suboptimal estimate of the optimal exercise strategy
. At sparse level 
both polynomial and piecewise linear basis functions deliver similar MWAO prices up to two decimal points after 
sample paths. At sparse level 
with 
sample paths the MWAO prices are the same up to three decimal point in both cases. Based on the results, both types of sparse basis functions solve our high-dimensional least squares problem and the prices converge to a level of 
at 
sample paths for sparse levels 
and sparse level
. Since the polynomial sparse basis functions are easier to construct and easier to implement, we recommend them as the bases of choice for our MWAO pricing problem.
The price of our moving average window option has three main sources of error: the number of simulation paths
, the level of the function basis 
and the number of integration samples
. The best possible approximation would have to reduce the errors originated from using these limiting parameters.
5. Conclusion
This paper presents a general and convergent algorithm for pricing early-exercisable moving window Asian options. The computational difficulty of the pricing task stems from what defines the option’s underlying: an either discretely or continuously sampled average over a moving window. We have applied a generalized framework to solve this high-dimensional problem by combining the least-squares Monte Carlo method with the
sparse grid basis functions. The sparse grid technique has been specifically developed as a cure to the “curse of dimensionality” problem. It allows more efficient selection of basis functions and can successfully approximate high-dimensional functions with less computational effort. We have used both the polynomial and the piecewise linear sparse basis functions in the least-squares regressions and found that the results converge to values up to two decimal points, independent of the type of basis functions used. We recommend the polynomial sparse basis as the basis of choice for this type of pricing problems since they are easier to construct and easier to implement. The approach presented in this paper can be generalized to pricing other high-dimensional early-exercisable derivatives that use a moving average as the underlying.
Appendix
ThetaML Implementation of the MWAO
This appendix gives a ThetaML (Theta Modeling Language)1 implementation of the MWAO pricing problem described in the text. To help understand the code, we first provide a brief description of the ThetaML language and some ThetaML specific commands and operators used in the models.
ThetaML supports standard control structures such as loops and if statements. It operates on a virtual timing model with the theta command. The theta command describes the time-determined behavior of financial derivatives. It allows time to pass. The fork command makes it possible to model simultaneous processes and enables cross-dependencies among the stochastic variables. The future operator “!” allows forward access to the future values of a variable, this operation is based on forward algorithms.
ThetaML modularizes the pricing task of MWAO into a simulation model for the stock prices and the numeraire, an exercise model for obtaining future early-exercise values, and a pricing model for computing the MWAO prices. ThetaML virtually parallels and synchronizes the processes—stock prices, numeraire, early exercise cash flows and MWAO prices—to the effect that it is as if these four processes step forward in time as they would have behaved in real life financial markets. ThetaML specific commands and operators are briefly explained in the models where they appear. Process variables in ThetaML models, such as “S”, “CUR”, “A”, implicitly incorporates scenarioand time-indices.
1 model StateProcesses
2 % This model simulates stock prices that follow a Geometric Brownian motion process
3 % and a numeraire process that are discounted at a constant interest rate;
4 % the arguments are in troduced into the model after the “import” keyword, results
5 % computed by the model are exported
6 import S0 “Initial stock prices”
7 import r “Risk_free interest rate”
8 import sigma “Volatility of stock prices”
9 export S “Stock price process”
10 export CUR “Numeraire process in currency CUR”
11
12 % initialize the stock prices at “S0”
13 S = S0
14 % initialize the numeraire at 1 CUR
15 CUR = 1
16 % “loop inf” runs till the expiry time of a pricing application
17 loop inf
18 % “@dt” extracts the smallest time interval from this model time to the next
19 theta @dt
20 % updates the GBM process of the stock prices for the time step “@dt”
21 S = S * exp((r - 0.5*sigma^2)*@dt + sigma*sqrt(@dt)*randn())
22 % update the numeraire for the time step “@dt”
23 CUR = CUR*exp(-r*@dt)
24 end
25 end
1 model MWAOExerciseValue
2 % This model computes the Early exercise values for MWAO, assuming daily exercises.
3 % Early exercises are possible after an initial allowance of a window length “m”
4 import S “Stock prices”
5 import CUR “Numeraire in currency CUR”
6 import m “Window length”
7 import T “Option maturity time”
8 export ExerciseValue “Exercise value”
9 export TimeGrid “A set of exercise times”
10
11 % initialize an array with length “m” to hold a past window of “m” stock prices
12 C = 0 * [1:m]
13 % initialize the moving average to “S/m”, where “S” are the time 0 stock prices
14 A = S/m
15 % initialize “C[m]” to the time 0 stock prices “S”
16 C[m] = S
17
18 ExerciseValue = 0
19 index = 1
20 % early exercise times range from “1/250” to “T”, equally spaced at “1/250”
21 TimeGrid = [1/250:1/250:T]
22
23 % “t” loops through the exercise time sand takes the value of the pointed element
24 loop t: Time Grid
25 % “theta” advances “t_@time” time units to the next time point
26 theta t_@time
27 % update the moving average by adding “S” evaluated at this time divided by “m”;
28 % at the end of “m” periods, subtract “S/m” evaluated at the start window time
29 A = A + S/m - C[index]/m
30 % record the stock price “S” at this time in “C”
31 C[index] = S
32 % increment the index by 1
33 index = index + 1
34 % reset “index” to 1 if “index” is bigger than “m”
35 if index > m
36 index = 1
37 end
38
39 % store the discounted exercise values for in-the-money paths
40 if @time >= 1/250 * (m-1)
41 ExerciseValue = max(A-S,0)*CUR
42 end
43
44 theta @dt
45 % reset Exercise Value to 0 at non-exercising times
46 ExerciseValue = 0
47
48 end
49 end
1 model MWAOPrice
2 % This model returns the MWAO prices across all the Monte-Carlo paths, using the
3 % early-exercise strategies obtained from the model MWAO Exercise Values
4 import Exercise Value “Exercise value”
5 import TimeGrid “A set of exercise times”
6 export Price “MWAO prices”
7
8 % at time 0, “Price” is assigned expected value of “value!”; the future operator “!” accesses the
9 % values of the variable “value” determine data later in stance
10 Price = E(value!)
11 % loop through the exercise times
12 loop t: TimeGrid
13 % early exercise evaluations, the “E” function computes the conditional expected
14 % discounted “value!”, using the Least Squares Monte Carlo regressions combined
15 % with the Sparse Grid type basis functions
16 if E(value!) < ExerciseValue
17 value = ExerciseValue
18 end
19 % time passing of “t-@time” with the “theta” command
20 theta t-@ time
21 end
22 % at the option maturity time, set the option pay off values
23 if ExerciseValue>0
24 value = ExerciseValue
25 else
26 value = 0
27 end
28 end
The stock prices and numeraire are first simulated in the external models “StateProcesses”, then imported as processes into the exercise model “MWAOExercise Values” to compute future early-exercise values. The early-exercise cash flows are next imported as a process into the pricing model “MWAOPrice” to determine the MWAO price.
The ThetaML future operator “!” appears in the model “MWAOPrice”. It allows the possibility to use the variable “value” at the model time when its values are not pre-assigned. Computationally, whenever the compiler encounters the future operator “!”, it evaluates the codes backward in time. So, when computing the time 0 option price, the compiler goes from the option maturity back to time 0, and assigns the computed time 0 value to “Price”.
NOTES
*ThetaML is a payoff description language that explicitly incorporates the passage of time. Product path dependencies, settlements, and early exercises are all appropriately addressed. ThetaML also offers the benefit to specify the complete structure of a structured product independent of the underlying stochastic processes. For details on ThetaML, please consult the references Dirnstorfer et al. [22], Dirnstorfer et al. [23] and Schraufstetter [24].