1. Introduction
Einstein’s lasting legacy is a geometry where space and time are woven into a single fabric. Rather than an abstract concept, geometry acquires an operational character, with light the defining actor. A spherical wave of light, perceived identically by all the inertial observers, is at the very foundation of Einstein’s Special Relativity. Further, Einstein’s General Relativity connects spacetime and gravity, with light’s trajectories manifesting the curvature of space-time.
Few other alternatives have been proposed to study and explore geometrical issues. A renown example is string theory. A string introduces a length, correlated with the string tension, and while classical strings live in all dimensions, “quantum strings” can live in specific number of dimensions. As a consequence the number of space dimensions became an open issue and a plethora of theories have been proposed living in extra dimensions [1-6]. One may wonder: Is there a natural explanation for the emerging large number of space dimensions? Should we suspect that quantum mechanics is associated to specific geometries?
In an historic and highly original approach, Cartan introduced spinors in order to obtain linear representations of different geometries [7,8]. This important idea was further expanded by Penrose, with spinor networks creating discrete space-time [9,10].
A profound sense of the foundations of geometry has been developed by Wheeler [11,12]. Wheeler considers that geometry is preceded by a stage named pregeometry, with pregeometry a network based on the calculus of propositions. Thus the entire geometrical edifice rests upon a form of logic.
Drawing from all these, we consider in the present work the geometry linked to a quantum spinor. We have indicated already [13] that the relational logic, or its equivalent formulation as a category theory, may serve as the common foundation of quantum mechanics and string theory. Category theory has been proven a fertile ground to address a variety of issues, like quantization of spacetime [14], attaching a formal language to a physical system [15], studying quantum information theory [16], exploring topological quantum field theories [17]. We have shown also that a relation (or a “morphism” in a category theory) may be represented by a spinor [18]. It is quite natural then to consider a composition of relations, or equivalently a composition of spinors, and following the Cartan-Penrose intuition to search for the corresponding geometry.
A single spinor gives rise to the Riemann-Bloch spin sphere, which is topologically equivalent to the null cone of Minkowski spacetime. We study the coupling of two Weyl spinors and the emerging geometry. There are two ways to couple two spinors, a Majorana-type coupling and a Dirac-type coupling. We find that the Majoranatype coupling leads to an entangled state respecting the well known entanglement rules. On the other hand the Dirac-type coupling generates an extra dimension, withing which two branes coexist. The emerging picture is quite similar to the ekpyrotic scenario [19-21], though in our case there is a significant difference. By construction, one brane hosts left-handed particles (our brane), while the other brane hosts right-handed particles. A distinct and interesting phenomenology is developed, based notably on the left-right symmetry embodied in the spacetime. The distance in the extra dimension is fixed by the amount of entanglement and if we consider that it may become a continuous variable, then we obtain the Milne geometry.
We should insist that we do not prove or derive a cosmological model, following Einstein’s legacy. Rather, by visiting the foundations of quantum mechanics and string theory, we explore the geometries consistent with entangled spinors. Geometry is not assumed but is the outcome of a quantum event. If a quantum string may indicate the number of space dimensions, then a quantum spinor may hint to the possible geometrical structures. We consider also that our study of coupled propositionsrelations-spinors is a concrete realization of Wheeler’s vision. A thorough exploration of the phenomenological implications of our proposal would be the best sign of its relevance.
2. Entanglement and Geometry
Consider the proposition-spinor . The relationship
. The relationship  is defined by [18]
is defined by [18]
 (1)
(1)
 receives the decomposition
receives the decomposition
 (2)
(2)
with 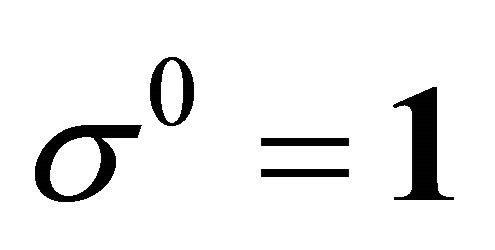 and
and 
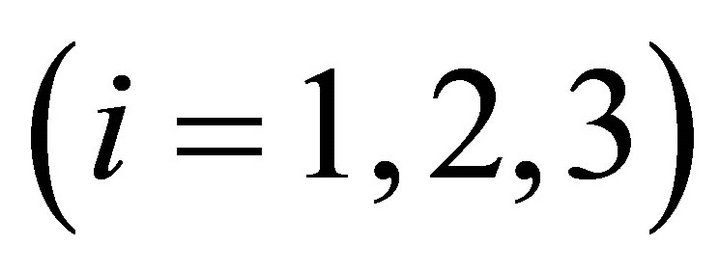 the Pauli matrices. We deduce that
the Pauli matrices. We deduce that
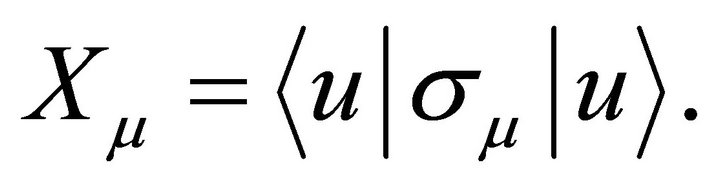 (3)
(3)
 satisfies identically the equation
satisfies identically the equation
 (4)
(4)
Equation (4) receives a double interpretation. It may represent a null vector belonging to Minkowski spacetime [7-10], indicating the logic-algebraic origin of Minkowski spacetime. On the other hand, with , it represents the spinor Riemann-Bloch sphere. Inversely, given Equation (4), we may search for its spinorial representations. We obtain the Cartan-Weyl equations
, it represents the spinor Riemann-Bloch sphere. Inversely, given Equation (4), we may search for its spinorial representations. We obtain the Cartan-Weyl equations
 (5)
(5)
 (6)
(6)
with  and
and  the left-handed and right-handed Weyl spinors.
the left-handed and right-handed Weyl spinors.
With a single spinor related to Minkowski spacetime, we may ask what kind of geometry emerges when we entangle two spinors. Lets consider first the Majorana type entanglement. Given a left-handed spinor , following Majorana’s recipe [22,23], we may construct a right-handed spinor
, following Majorana’s recipe [22,23], we may construct a right-handed spinor 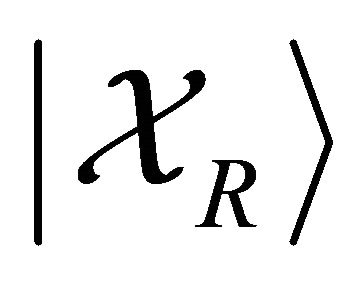 by
by
 (7)
(7)
Starting with two left-handed Weyl spinors
 (8)
(8)
we define the four-component Majorana spinor
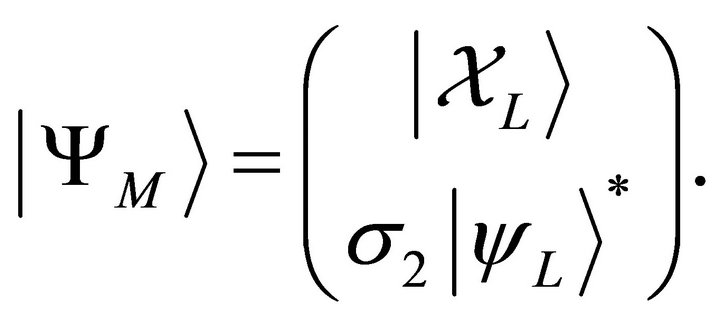 (9)
(9)
With  we find
we find
 (10)
(10)
 (11)
(11)
 (12)
(12)
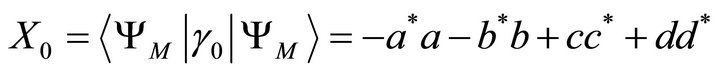 (13)
(13)
where we used
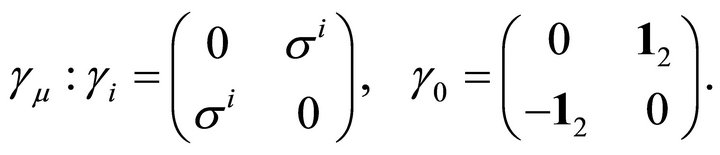 (14)
(14)
The quantity 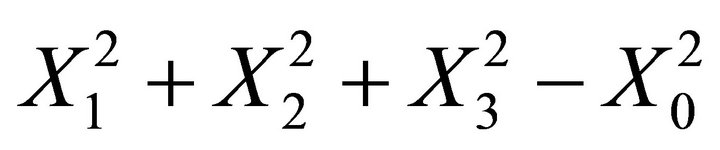 is not anymore zero. We find
is not anymore zero. We find
 (15)
(15)
Considering


with
 (16)
(16)
we obtain
 (17)
(17)
The requirement that the Riemann-Bloch sphere remains intact, Equation (4), implies the condition
 (18)
(18)
The above condition guarantees that there is no coupling between the upper spinor and the lower spinor composing the Majorana spinor, Equation (9). Equally well the quantity 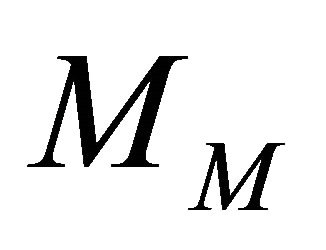 is a direct measure of entanglement in its own right.
is a direct measure of entanglement in its own right.
The usual description of a two-qubit pure state is to write, in an obvious notation,
 (19)
(19)
To measure the inherent entanglement, it has been proposed to make use of the “concurrence” [24]. The concurrence C involves the spin-flipping of spinors, in direct analogy to the time honored Majorana’s reversal of handedness (see our Equation (7) ). In both ways we obtain the same estimate for the entanglement, though the framework of derivation is different. In another direction the two-qubit entanglement has been studied by making appeal to quaternions [25]. A Hopf fibration, from the seven dimensional sphere 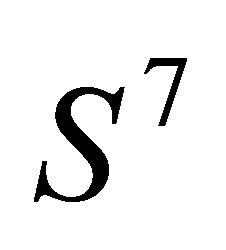 to the four dimensional sphere
to the four dimensional sphere , allows to set aside the global phase degrees of freedom. An operator, termed “entanglor”, provides an estimate for the entanglement identical to ours
, allows to set aside the global phase degrees of freedom. An operator, termed “entanglor”, provides an estimate for the entanglement identical to ours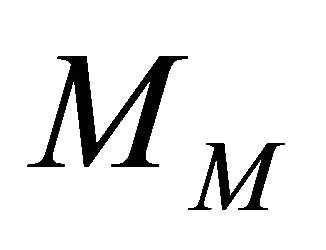 . Thus our Majorana entanglement reproduces the ordinary two-qubit entanglement [24-27], offering furthermore a space-time picture of the process.
. Thus our Majorana entanglement reproduces the ordinary two-qubit entanglement [24-27], offering furthermore a space-time picture of the process.
For the Dirac entanglement we select a left-handed Weyl spinor and a right-handed Weyl spinor. Writing
 (20)
(20)
and
 (21)
(21)
we obtain
 (22)
(22)
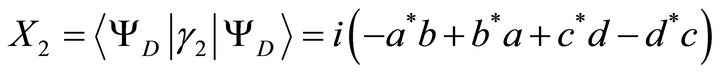 (23)
(23)
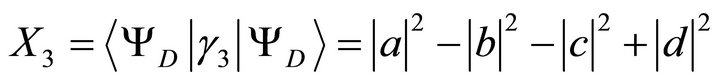 (24)
(24)
 (25)
(25)
The quantity  is not anymore zero. We obtain
is not anymore zero. We obtain
 (26)
(26)
Considering


we find
 (27)
(27)
The absence of entanglement and the re-establishment of the Riemann-Bloch sphere is obtained, when the condition
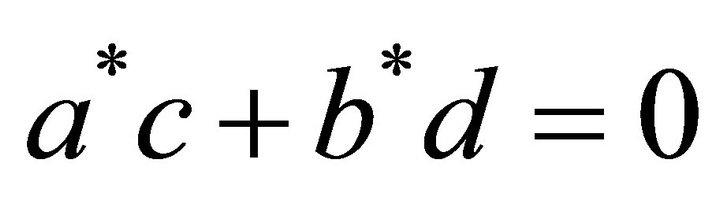 (28)
(28)
is fulfilled. The above condition certifies the absence of a coupling between the upper left-handed spinor and the lower right-handed spinor, Equation (21), or equivalently the absence of a mass term.
Notice the different character of Majorana entanglement and Dirac entanglement. Majorana entanglement couples two left-handed (or two right-handed) spinors, while Dirac entanglement couples a left-handed spinor and a right-handed spinor. Also in the Majorana case  lies outside the null cone of Minkowski spacetime, while in the Dirac case
lies outside the null cone of Minkowski spacetime, while in the Dirac case  lies inside the null cone.
lies inside the null cone.
Let us define ,
, . The Dirac entanglement, Equation (26), takes then the form of a space-like hyperboloid
. The Dirac entanglement, Equation (26), takes then the form of a space-like hyperboloid
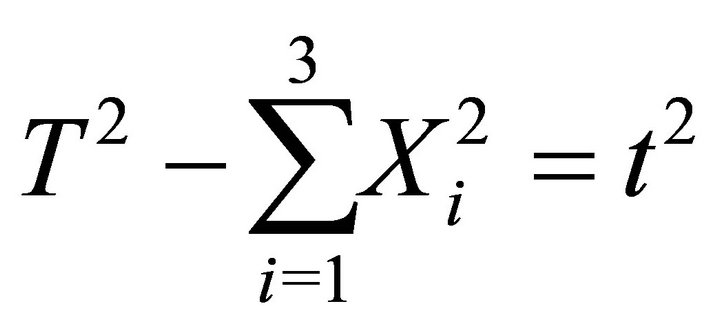 (29)
(29)
A comparison with the previous null cone geometry, indicates that quantum entanglement, specified and quantified by t, generates an extra dimension. The distance along this extra dimension indicates how far we are from the null cone. Furthermore our space-time acquires a double-sheet structure, reminding the ekpyrotic model where two branes coexist. There is though a distinct difference. In our model, by construction, one brane hosts left-handed particles (our brane), while the other brane hosts right-handed particles.
For a a specific quantum spinor the amount of entanglement t is fixed. Still we may imagine that we “tune” t and consider t as a continuous variable. A varying t will offer us a continuous foliation of the internal space of the null cone. We can adopt a reparametrization, satisfying automatically Equation (29) and leading us to the four independent dynamical degrees of freedom
 (30)
(30)
The induced metric becomes then
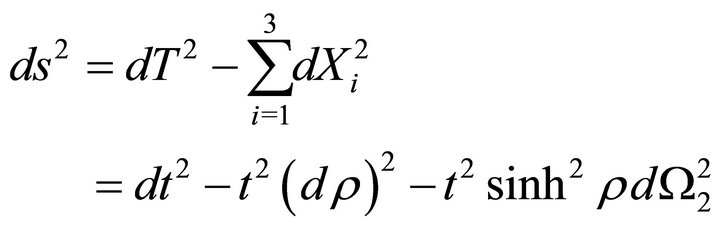 (31)
(31)
representing a Milne universe.
We have opted to use alternative ways in studying spacetime geometries, next to the well established and checked Einstein’s General Relativity. Geometry and the number of dimensions are not abstract, mathematical constructions, but the outcome of a quantum event. Studying geometries consistent with quantum entanglement has its own merit and in the next section we consider the phenomenological implications.
3. Phenomenology
Everything is under evolution. Ordinary matter and radiation, stars, galaxies, clusters of galaxies emerge as parts of an unfolding cosmic evolution. Within this process of universal evolution, should we evolve our own notions of space and time? Is spacetime itself an emergent property of a deeper theory or, to use Wheeler’s terminology, it originates from a pregeometry? The close connection we found between a relation and a spinor, led us to follow the Cartan-Penrose argumentation [7-10,28, 29] and use the relation-spinor as the building block of space-time. If a single spinor is associated to Minkowski space-time, our study indicates that the entanglement of two spinors gives rise to a more complex space-time. At first quantum entanglement generates an extra dimension, indicating that a quantum system in d dimensions is analogous to a classical system in d + 1 dimensions [30]. Further within the extra dimension two 3-dimensional branes coexist. The outcome is very similar to the ekpyrotic model [19-21]. According to the ekpyrotic scenario a violent collision between the two branes results to a conflagration, resembling the conventional “big bang”. It should be noted though that the ekpyrotic model is derived within the heterotic M-theory [31,32], while the universe we suggest emerges out of a quantum logical process. Furthermore the two branes are not identical in our case. By construction one brane hosts left-handed particles (our brane), while the other brane hosts righthanded particles. Considering that the amount of entanglement is a continuous variable we obtain the Milne geometry.
The Lagrangian for a particle in a Milne universe is
 (32)
(32)
The equations of motion are easily solved in the case of one-dimensional branes. We find
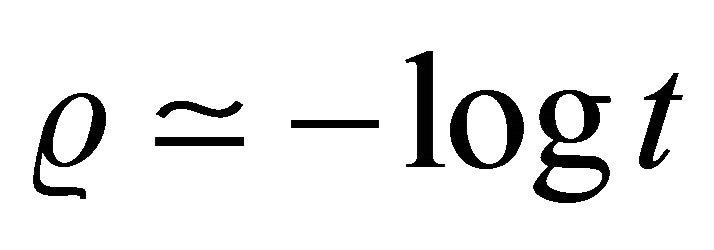 (33)
(33)
As  goes to zero we approach the time of branecollision (the ekpyrosis moment) and the distance
goes to zero we approach the time of branecollision (the ekpyrosis moment) and the distance  across the brane becomes infinite. We gather that at the collision time the correlation along the brane is infinite and all the points in the brane are causally connected [33]. The apparent homogeneity and isotropy of our universe can be accounted therefore, making less pressing the need for an inflantionary scenario [34,35].
across the brane becomes infinite. We gather that at the collision time the correlation along the brane is infinite and all the points in the brane are causally connected [33]. The apparent homogeneity and isotropy of our universe can be accounted therefore, making less pressing the need for an inflantionary scenario [34,35].
The conventional way to restore left-right symmetry is to introduce an extra  gauge group in the energy desert above the scale of the standard
gauge group in the energy desert above the scale of the standard  interactions. The right-handed gauge bosons are more massive compared to the left-handed gauge bosons, leading to parity violation at low energies [36,37]. Within our approach the left-right symmetry is achieved with the extra dimension hosting two “mirror’’ branes, a lefthanded brane and a right-handed brane. Higgs scalars, denoted by
interactions. The right-handed gauge bosons are more massive compared to the left-handed gauge bosons, leading to parity violation at low energies [36,37]. Within our approach the left-right symmetry is achieved with the extra dimension hosting two “mirror’’ branes, a lefthanded brane and a right-handed brane. Higgs scalars, denoted by  and
and , live in the corresponding branes, though having different vacuum expectation values. An interaction term
, live in the corresponding branes, though having different vacuum expectation values. An interaction term  may induce a mixing of the two Higgs scalars, serving also as a mediator between the two branes. At the ekpyrotic moment
may induce a mixing of the two Higgs scalars, serving also as a mediator between the two branes. At the ekpyrotic moment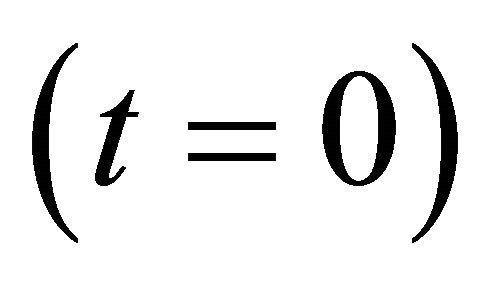 , the full conformal
, the full conformal 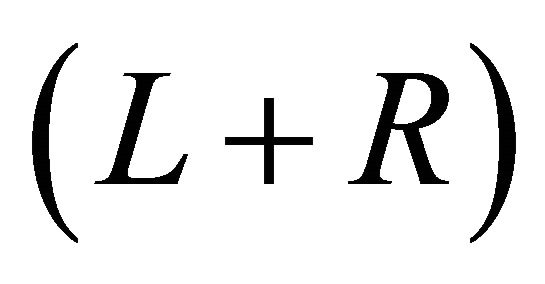 symmetry is achieved. From a phenomenological point of view the particles living in the “other” brane behave as mirror-duplicate of the particles in our visible world [38,39].
symmetry is achieved. From a phenomenological point of view the particles living in the “other” brane behave as mirror-duplicate of the particles in our visible world [38,39].
The most prominent candidate for mediation between the two branes is the neutrino particle. The left-handed neutrino, an essential ingredient of the standard model, resides in our brane, while its counterpart, the righthanded neutrino, resides in the other brane. The two braneworlds are equivalent to a two-sheeted spacetime  [39,40], with
[39,40], with 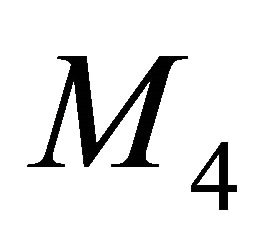 standing for a four-dimensional continuous manifold and the fifth dimension reduced to two discrete points separated by a distance
standing for a four-dimensional continuous manifold and the fifth dimension reduced to two discrete points separated by a distance  (the amount of entanglement). The neutrino mass matrix involves Majorana mass terms coupling neutrinos residing in the same brane and Dirac mass terms coupling neutrinos across the branes. The actual neutrino masses emerge then in a natural way. The well known phenomenon of neutrino oscillations acquire a novel character as a swapping between the branes [41]. Notice also the evolving nature of the neutrino mass. Close to ekpyrosis the Dirac neutrino is massless, affecting in a distinc way cosmology.
(the amount of entanglement). The neutrino mass matrix involves Majorana mass terms coupling neutrinos residing in the same brane and Dirac mass terms coupling neutrinos across the branes. The actual neutrino masses emerge then in a natural way. The well known phenomenon of neutrino oscillations acquire a novel character as a swapping between the branes [41]. Notice also the evolving nature of the neutrino mass. Close to ekpyrosis the Dirac neutrino is massless, affecting in a distinc way cosmology.
In our universe we register three main components. Visible matter accounts for about 4%, dark matter for 21% and dark energy for the remainder. In the usual approach we consider that dark matter consists of particles (classified as cold, warm, hot), while the dynamics of dark energy is assumed by the cosmological constant . In our case we explain dark matter and dark energy by invoking geometry. Everything that is localized in the other brane and in the extra dimension appears dark to us. If we assume that in our observed brane, matter is equally shared between visible and invisible matter, with the same analogy holding in the other brane, then we obtain naturally that our visible matter is ~1/5 of the entire matter content, in agreement with the observations. Similar arguments have been developed in models where the brane is folded many times inside the extra dimension [42]. Since we have located most of the matter outside our brane, we may easily imagine that the local distribution of visible matter is not identical to the local distribution of the entire matter. In an imaginative journey, as we leave the center of our galaxy, moving a fraction of the millimeter across the extra dimension to reach the “other” brane, we are not going to land at the center of the “other” galaxy. The local matter distribution in the “mirror” brane is not the same with the matter distribution in our brane, and the net effect is a displacement of the dark matter density with respect the visible matter density. Such an effect has been recently observed. The peak of the local dark matter density differs from the center of our galaxy by several hundred parsec [43].
. In our case we explain dark matter and dark energy by invoking geometry. Everything that is localized in the other brane and in the extra dimension appears dark to us. If we assume that in our observed brane, matter is equally shared between visible and invisible matter, with the same analogy holding in the other brane, then we obtain naturally that our visible matter is ~1/5 of the entire matter content, in agreement with the observations. Similar arguments have been developed in models where the brane is folded many times inside the extra dimension [42]. Since we have located most of the matter outside our brane, we may easily imagine that the local distribution of visible matter is not identical to the local distribution of the entire matter. In an imaginative journey, as we leave the center of our galaxy, moving a fraction of the millimeter across the extra dimension to reach the “other” brane, we are not going to land at the center of the “other” galaxy. The local matter distribution in the “mirror” brane is not the same with the matter distribution in our brane, and the net effect is a displacement of the dark matter density with respect the visible matter density. Such an effect has been recently observed. The peak of the local dark matter density differs from the center of our galaxy by several hundred parsec [43].
Gravity is not confined to the brane and matter fields on the brane can emit gravitational waves into the bulk. The brane energy-momentum tensor is not conserved therefore and it is essential to include this energy flow into realistic cosmological models. The leakage of gravitational energy into extra dimension affects the cosmological expansion [44], inducing an accelerating expansion for the three dimensional space [45-47]. Thus an alternative to the non-zero cosmological constant scenario is offered.
It is well known that life manifests a strong biohomochirality. In the living organisms we encounter only lefthanded aminoacids and right-handed sugars. There are many hypotheses advanced regarding the origin of biohomochirality. We would like to point out the hypothesis linking the bio-asymmetry to the fundamental parity violation of the weak interactions. The weak neutral currents (mediated by Z0) stabilize preferentially the L-aminoacids and D-sugars over the D-aminoacids and L-sugars. The difference in energy between the two enantiomers is small. A phenomenon of autocatalysis in a far from equilibrium state, amplifies the small difference and in a period of 104 years leads to a unique chirality [48,49]. If this working hypothesis is a valid one, then in the “mirror” brane the corresponding weak neutral currents will operate in the opposite direction. In that case the lifeforms of the other brane will have exclusively D-aminoacids and L-sugars.
4. In Lieu of Conclusions
Quantum mechanics and string theory display a highly relational nature, with both of them sharing the same relational logic [13]. Our representation of a relation by a spinor allowed us to connect logic with geometry and space-time. We found that the entanglement of two spinors generates an extra dimension and the distance in the extra dimension is measured by the amount of entanglement. Finally two brane-geometries are entangled together: one brane hosting left-handed particles and another brane hosting right-handed particles. We would like to draw also a parallel with the CFT/AdS duality [50,51]. A spinor may be viewed as the space-time orientation of a pixel on a holographic screen [52]. Through the pixel on the light-cone a null ray passes. What the quantum entanglement offers us is the exploration of the internal space of the light-cone (the bulk). On very general grounds it has been shown the correspondence between quantum entanglement, classical renormalization group and holographic gauge/gravity duality [53-56]. The stringy degrees of freedom operating in the CFT/ AdS duality are assumed in our case by the entanglement degrees of freedom and quantum phenomena are encoded in classical geometry.
The emerging geometry offers a rich phenomenology: a novel way to approach left-right symmetry on cosmological scale, a link of dark matter and dark energy to the dynamics of extra space, particles and forces as mediators between the branes, a connection between the leftright symmetry breaking and biohomochirality. Within our approach time acquires a new role. The beginning of time is not set at the “big bang”, 13.7 billions years ago, but somehow is lost in the previous aeons. The time allocated to universe’s evolution is longer than 13.7 billion years, involving also the time periods between successive “ekpyrotic” moments. During these periods-aeons part of the creation of the universe was carried out. Thus the difficulty in accommodating the different distinct phenomena within a single history, exemplified by the account of the “anthropic principle” [57,58], is significantly reduced. Searching for the ruins from a previous aeon, or the archeology of the universe, is the most intricate and complicated task. Yet, it has been already suggested that in the CMB there are traces from an activity preceding the “big-bang” [59].
Altogether our approach offers links between logic— quantum mechanics—cosmology and allows addressing foundational questions regarding the evolution of the universe. A relevant phenomenology may serve as the testing ground of these ideas.
5. Acknowledgements
One of us (A.N.) would like to acknowledge useful discussions with Prof. Brian Schmidt and Prof. Ernest Ma during the 16th Paris Cosmology Colloquium. The present work is supported by the Templeton Foundation.