Einstein-Podolsky-Rosen Steering and Nonlocality in Open Quantum Systems ()
1. Introduction
Quantum entanglement (QE) has emerged as a fascinating subject and a fundamental aspect of quantum mechanics since the pioneering efforts of Einstein and colleagues [1] . This phenomenon represents a type of non-local correlation manifesting in the inseparability of states, and it has played a significant role in advancing key tasks in quantum information processing and transmission [2] - [8] . Notably, correlations derived from local measurements on entangled systems can exhibit nonlocal properties [9] . The theory of local hidden variables imposes constraints on the measurement statistics for a broad set of quantum systems [10] . Nonlocality, an essential feature of QE, was highlighted through the “EPR paradox,” central to understanding nonlocality [1] . This paradox questions quantum theory’s ability to explain what has been termed “spooky action at a distance.” Schrödinger further elucidated this by introducing the concept of quantum steering (or EPR steering), which allows local measurements to control a distant quantum subsystem without direct interference [11] . Quantum steering (QS) is widely applied as a quantifier of the quantum correlation that exhibits the Einstein-Podolsky-Rosen (EPR) paradox. In the field of modern quantum information theory, it is considered a form of quantum correlation between quantum entanglement (QE) and Bell’s nonlocality. Entangled states are regarded as a superclass of steerable states [12] . Recently, QS has attracted significant attention in both experimental and theoretical research [13] - [19] . Steerable states can be applied in channel discrimination [20] , cryptography [21] , and teleportation [22] . Additionally, Quantum Steering (QS) is attributed to operational descriptions [23] . Both discrete and continuous quantum systems exhibit some QS inequalities, which are derived using the uncertainty relation in terms of entropy [24] [25] [26] . There have been significant experimental and theoretical developments aimed at explaining this form of nonlocality [25] [26] [27] [28] . Among these developments, significant standards for QS have been established by demonstrating QS in various aspects [29] [30] . The study of the Bell plan facilitates the expression of Bell-like inequalities for QS. Furthermore, the criteria for QS utilize the relationship between Quantum Entanglement (QE) and the uncertainty relation [29] [30] .
In addition to characterizing and quantifying correlations, understanding the behavior of these correlations under the influence of decoherence is another significant issue. Practical quantum systems inevitably interact with their surroundings, which during their dynamical evolution leads to decoherence [31] . In recent decades, studies have primarily focused on relaxation and dephasing in Markovian and non-Markovian open quantum systems. Consequently, dynamic evolution is an important property of quantum systems, which renders the quantum of finite time intriguing [32] . In nearly all models used to depict open quantum systems, the coherence of a state asymptotically descends to zero. Additionally, the entanglement dynamics often exhibit sudden death in a decoherent environment [33] . Thus, the asymptotic dynamics of various physical quantities offer ideal systems for examining the quantum properties crucial to information and quantum optics. Various systems, including quantum dot systems [34] [35] [36] [37] [38] , impurity systems [39] [40] [41] [42] [43] , and trapped ions [44] [45] [46] , implement these architectures. The performance of quantum properties is often characterized by environmental noise present in quantum systems. Therefore, developing a method for estimating noise levels is critical to mitigate the phenomenon of decay under decoherence. Controlling the environmental conditions of a quantum system is essential for managing its degradation effects. In this manuscript, we investigate the dynamical behavior of quantum systems (QS), Bell nonlocality, and quantum entanglement (QE) in open quantum systems. We examine the development of a two-qubit system within the framework of Kossakowski-type quantum dynamical semigroups. This study highlights how the fundamental criteria of the quantum model impact the quantumness measures of the asymptotic states. We present various scenarios where the asymptotic states exhibit steerability, entanglement, and Bell nonlocality. Additionally, we demonstrate the resilience of quantum measures of correlations against environmental influences, maintaining their integrity over extended periods.
The manuscript is organized as follows: Section 2 discusses the measures of quantumness, which describe the quantum correlations. Section 3 introduces the quantum model for the open quantum system and presents the numerical results. A summary is provided in the final section.
2. Quantum Steering, Quantum Nonlocality and Nonlocal Correlation
The local hidden state model for discrete observables has been developed [25] [26] [30] . Through the consideration of the positivity of the relative entropy, it is possible to evaluate the local hidden state constraints in the scenario involving discrete variables: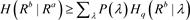 , here
(
) and
(
) represent, respectively, discrete observables with outcomes
(
) and
(
).
describes the discrete Shannon entropy of
with
. The steering inequality for the discrete variables is acquired by [30] :
, here
(
) and
(
) represent, respectively, discrete observables with outcomes
(
) and
(
).
describes the discrete Shannon entropy of
with
. The steering inequality for the discrete variables is acquired by [30] :
. (1)
For quantum systems defined in two dimensional space, the inequality of the entropy uncertainty relation (EUR) steering is given by [30]
(2)
where QS occurs when the inequality is violated. Consider a bipartite system of qubits in the X-state
(3)
where
are real. By performing a convenable local unitary transformation, the state
defined in equation (3) according to the Bloch decomposition can be written as
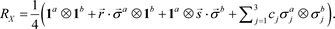 (4)
(4)
where
and
are the vectors of Bloch and
representing the Pauli matrices. Then, based on the definition of the QS inequality in equation (2) and using the matrix state
in equation (3), the QS inequality in the context of Pauli measurements is given by [47]
(5)
where
with
are the diagonal (
) and anti-diagonal (
) elements of the state
. Additionally, an inequality has been developed to assess whether a bipartite quantum state is steerable [29] . Recently, Cavalcanti et al. proposed other parameters for the quantification of Quantum Steering (QS) [48] . Subsequently, a measure of steering was introduced, taking into account the maximal violation of the steering inequalities [49] .
We introduce the Bell Clauser-Horen-Shimony-Holt (CHSH) to test the quantum nonlocality. As stated by the Horodecki criterion [10] ,
with
. The elements
design the eigenvalues of
with
is obtained from the coefficients [10] [50]
. (6)
Their eigenvalues are given by
It is obvious to note that
is greater than
, and then the Bell inequality maximum violation is introduced by the formula [47]
(7)
We utilize the entanglement of formation (EOF) developed by the Wootters [51] [52] to exhibit the entanglement in the qubits state
(8)
where the function
is stated by
(9)
and the concurrence by
(10)
where
define the eigenvalues of
in decreasing order and
is given by
(11)
where
is the complex conjugate of R. The degree of QE varies from
for the case of separables states to
for the case of Bell states.
3. Asymptotic States and Numerical Results
In this section, we present the physical model of asymptotic quantum states, considering a system that evolves according to Kossakowski-type quantum dynamical semigroups. Furthermore, we provide results describing the evolution of the quantifiers.
Consider two qubits placed in an environment, analyzed using standard weak-coupling limit techniques [53] . The reduced irreversible quantum dynamics of this system is characterized by a single parameter known as quantum dynamical semigroups, represented by
. The behavior of this system is described by the master equation:
where the generator L accounts for the influences of the external environment through the elements of the Kossakowski matrix [53] [54] [55] . Officially, we have
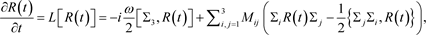 (12)
(12)
where the parameter
designs the system frequency,
,
is the 2 × 2 identity matrix,
represent the Pauli matrices and the M matrix is given by
(13)
This illustrates that the semigroup obtained by using the main equation includes purely positive maps
for all
. Using
and
, the fully dissipative contribution to the quantum state is
(14)
In this manner, there exist six Kraus operators
(
;
) and
6 × 6 Kossakowski matrix is written
(15)
From open systems theory [53] [56] , the coefficients
related to the ith Pauli matrix of the αth qubit and, respectively, the jth Pauli matrix of the βth qubit,
;
, are defined through the use of Fourier transorms of the time-correlation functions with regard to the equilibrium state of the environment.
Now, we are going to examine the temporal evolution of the two qubits defined initially in the state
(16)
Here the parameters A, B, C and D are considered to be real constants with the normalization condition
, and that elements
form an orthonormal basis related to the basis
by
(17)
Here
and
define the Bell states.
The density matrix (16) can be represented as
(18)
Equation (18) is entangled when
or
. The both conditions cannot be met at the same time. The density operator (18) covers a large family of states for the system of qubits, including Bell states [57] [58] , Werner states [59] , Horodecki states [59] , and so on.
The temporal evolution of
can be obtained as
(19)
where the time-dependent coefficients are given by
(20)
with
(21)
It is acknowledged that, in certain situations, the coupling of the environment does not necessarily destroy coherence but can instead generate it. This phenomenon may also be observed in the current model due to the reduced dynamics described in equation (12).
We now examine three classes of correlations in the asymptotic dynamics for different families of initial states. Based on equations (6), (8), and (9), we demonstrate the performance of Quantum Steerability (QS), Quantum Nonlocality, and Quantum Entanglement (QE) in qubit states with respect to the parameters of the model. The quantum correlations for diverse sets of initial states, assuming various values of the parameter γ, are depicted in Figures 1-3. Generally, it is observed that changes in the parameter γ significantly affect the quantum dynamics and the measures of quantum correlations for different states.The measures of the Bell nonlocality and Quantum Steering (QS) can exhibit similar behavior during their time evolution.It is interesting to note that by carefully selecting the parameter
and the initial state of the two qubits, we can control and manipulate these quantum measures in the asymptotic dynamics. When starting with an initial separable state of two qubits, we observe that the state of the qubits is unsteerable and does not demonstrate quantum nonlocality, despite the generation of entanglement, as illustrated in Figure 1. This indicates that both steering and Bell nonlocalities, starting from the initial separable state, are satisfied and accompanied by an entangled state in the asymptotic dynamics, for different values of γ. In the case of an initial Horodecki state, the quantum measures firstly decrease from their maximal value, where the two qubits’ state is maximally steerable (for the case of
), quantum nonlocality with the Tsirelson bound and maximally entangled state, and thereafter the measures decrease with the time exhibiting the sudden death phenomenon of entanglement with the absence of QS and Bell nonlocality. We obtain that QS and Bell nonlocality disappear before the entanglement. Moreover, we observe that the change in the parameter γ does not largely affect the behaviour of the quantum measures during the dynamics, as seen in Figure 2. In the third example, specifically for an initial Werner state, we observe that the qubits’ state exhibits steerability and Bell nonlocality, indicating the presence of entanglement during the asymptotic dynamics. This observation is depicted in Figure 3 for the case of
, where both CHSH and steering inequalities are violated, confirming the entanglement of the qubits’ state. Conversely, for the case of
as presented in Figure 3, the qubits’ state remains entangled without violating steering and CHSH inequalities. Additionally, variations in the values of γ can enhance the correlations throughout the dynamics.
![]()
Figure 1. Asymptotic dynamics of the correlations for the initial state,
, is plotted as a function of the time t for
and
. The axis
represents the case for which the QS inequality defined in equation (5) holds the value 2. The blue dash-dotted curve displays the variety of the QS inequality, red dashed curve represents the variation of the Bell inequality and green solid line shows the variety of the QE. The panel (a) is for
and panel (b) is for
.
![]()
![]()
Figure 2. Asymptotic dynamics of the correlations for the initial Horodecki state,
, is plotted as a function of the time t for the case of
(entangled state) and
(bell state). The blue dash-dotted curve displays the variation of the QS inequality, red dashed curve represents the variation of the Bell inequality and green solid line shows the variety of the QE. The panels (a) and (b) are respectively for
and
with
(bell state). The panels (c) and (d) are respectively for
and
with
(entangled mixed state). The axis
represents the case for which the QS inequality defined in equation (5) holds the value 2.
![]()
![]()
Figure 3. Asymptotic dynamics of the correlations for the initial Werner state,
, is plotted as a function of the time t for the case of
and
. The blue dash-dotted curve displays the variation of the QS inequality, red dashed curve represents the variation of the Bell inequality and green solid line shows the variety of the QE. The panels (a) and (b) are respectively for
and
with
. The panels (c) and (d) are respectively for
and
with
. The axis
represents the case for which the QS inequality defined in equation (5) holds the value 2.
4. Conclusion
We have investigated the dynamic behavior of quantum steering (QS), Bell nonlocality, and entanglement of formation in open quantum systems. Our study introduced a system comprising two qubits within the Kossakowski quantum dynamical semigroup framework. It was demonstrated that the quantum characteristics of the asymptotic states are influenced by the primary parameter of the model under consideration, and that manipulation of these characteristics can be achieved through careful selection of these parameters. Our analysis spanned various scenarios, encompassing Werner states, Bell states, and Horodecki states, wherein the asymptotic states exhibit steerability and entanglement, coupled with Bell nonlocality. Additionally, we demonstrated that the three measures of quantum correlations are capable of withstanding the effects of external environments, thereby preserving their integrity over extended durations.