1. Introduction
Recently, we proposed the quaternion time theory [1] , which seems to show promise in describing spacetime in arbitrary frames of reference. In addition, the quaternion theory of time addresses the optical Doppler effect [2] , as initially analyzed mathematically by Voigt [3] and experimentally demonstrated by Ives and Stilwell [4] [5] .
Similar to the theory of time, the present work adopts the Euclidean division algebra postulate, stating that division algebras with Euclidean norm, consisting of real numbers, complex numbers, real quaternions, and octonions, are essential mathematical tools of nature. Note that higher order normed division algebras are not possible based on the theorems of Frobenius and Hurwitz [6] [7] .
It seems remarkable that from the beginning, Maxwell attempted to summarize electromagnetic equations in a four-dimensional form using real quaternions [8] and [9] , which were originally introduced by Hamilton [10] and [11] . Clearly, this effort had only limited success primarily because of the lack of a comprehensive quaternion spacetime theory and the absence of a suitable quaternion calculus during Maxwell’s lifetime.
Eventually, the original Maxwell equations were significantly modified, particularly by Heaviside [12] , who changed the four-dimensional mathematical formalism of Maxwell to favor a three-dimensional real vector representation. While this effort made Maxwell’s equations significantly more accessible mathematically, some of the key results of Maxwell’s theory became significantly modified, particularly those related to the electromotive force and electromagnetic current expressions [13] [14] .
Historically, various forms of quaternion analysis have been applied to derive Maxwell’s equations in quaternion form. However, most studies used complex bi-quaternions, where each of the four quaternion parameters is represented by a complex number. This was initially proposed by Conway [15] [16] , and Silberstein [17] [18] , who demonstrated that the bi-quaternion form of relativity and Maxwell equations can be reconciled with the Minkowski spacetime [19] . More recently, the bi-quaternion approach inspired several representations of Maxwell’s equations by Waser [20] , and Arbab [21] [22] . Also, a bi-quaternion form of quantum mechanics was proposed by Adler [23] , and was further extended by Horwitz [24] [25] . Recently, several publications on quaternion quantum electrodynamics and the unification of Maxwell equations with Dirac were presented by Chanyal [26] [27] [28] .
The bi-quaternion approach introduces additional degrees of freedom and additional numerical parameters in comparison with the original real quaternion division algebra, where each of the four quaternion parameters is a real quantity. However, the complex bi-quaternion extension of the real quaternion algebra is no longer a normed division algebra, and consequently will not be used in the present work.
In the present study we only use normed division algebras, as defined by Frobenius and Hurwitz; consequently, we limit our development to real quaternions only. We do not seek compatibility with the Minkowski spacetime, because we developed an alternative fully functional formulation of the spacetime using the real quaternion time [1] .
Note that a real quaternion differentiation procedure was empirically proposed and discussed by Deavours [29] , Jack [30] , and Dunning-Davies [31] , which resulted in a close resemblance of the quaternion expressions to the modified version of Maxwell’s equations.
In this study, we embark on the development of a suitable quaternion differentiation procedure that can be applied to any physical system. We propose a quaternion path derivative and gradient operator and apply them to the quaternion electromagnetic potential. We postulate that the first derivative results in an electromagnetic force field, similar to the traditional Lorentz force. We then assume that the second derivative, represented by the quaternion Laplacian, is equal to the quaternion current density. We show that the new equations can be written equivalently in terms of the quaternion electromagnetic potential as well as the quaternion electromagnetic fields, thus reconciling the differences between the potential and field representations of electromagnetism pointed out by Aharonov and Bohm [32] . The new equations represent action at a distance due to the quaternion time formulation and consequently automatically account for the retarded potentials.
We show that the new scalar electric field, which is missing in the original version of Maxwell’s equations, leads to a conduction current, which we identify as a new form of Ohm’s law. In addition, we show that the sign of the electrical displacement current in the modified version of Maxwell’s equations does not agree with our analytical version of the electromagnetic equations. However, we demonstrate that the resulting analytical electromagnetic equations are in good agreement with the original version of Maxwell’s equations.
Because, real quaternions can be written in the normal or complex conjugate form, we suggest that this dual representation corresponds to the expression of the electromagnetic laws in the reference frames of a signal transmitter and receiver.
2. Transmitter and Receiver Coordinate Systems
We begin our study by analyzing a physical experiment in which a transmitter of electromagnetic interaction sends a signal to a receiver, which may be located some distance from the transmitter.
When both the transmitter and receiver are located at the same location, which we consider as the origin of the coordinate system, the time of signal emission by the transmitter,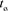 
, is a real scalar quantity equal to the time of signal detection by the receiver,
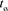. Next, we consider the time delay, which is equal to the difference between the times of signal detection and emission, for the receiver and transmitter separated by a vector distance,
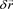. Naturally, this delay is due to the maximum speed of any electromagnetic signal propagation, which is assumed to be equal to the speed of light, c. Therefore, we can introduce the concept of time at a distance to account for the time delay between the transmitter and receiver of electromagnetic interaction. Remarkably, Lorentz introduced the concept of four-dimensional local time to address the issue of time delay [33] [34] . Later, Einstein abandoned the concept of local time in favor of the four-dimensional non-Euclidean spacetime [19] . However, the concepts of action at a distance and time at a distance, continued to be of interest and were expressed as retarded potentials by Lienard [35] , Wiechert [36] , and Jefimenko [37] . In the retarded potentials approach, time at a distance is represented by a real scalar value, which neglects the three-dimensional nature of space.
Recently, we suggested [1] that Euclidean normed division algebras are essential for the representation of physical reality. Consequently, we used a Euclidean quaternion representation of time intervals, as an alternative to non-Euclidean spacetime.
To demonstrate the quaternion time, we again consider a stationary transmitter of the electromagnetic signal at the origin, while the receiver is located at a vector distance,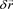 
, away from the origin. Again, we assume that the real scalar time, 
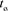, is the time of the signal emission by the transmitter at the origin. In addition, we assume that the time-of-flight of the electromagnetic interaction in three-dimensional space can be expressed as a three-dimensional vector, 
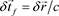. Then, we suggest that the following quaternion time expression represents the time of electromagnetic signal arrival at a distance,
(1)
A three-dimensional space representation of the transmitter reference frame is shown in Figure 1.
![]()
Figure 1. Time delay of an electromagnetic signal propagation from a transmitter at the origin to a receiver at a distance, 
, in the transmitter reference frame.
Alternatively, we can move the origin of the coordinate system to the location of the signal receiver. Now, the signal transmitter is located at a distance of,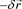
. Then, we can define the remote time at the transmitter location as,
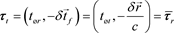(2)
assuming that we performed a clock synchronization procedure [1] , such that,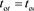
. We show a three-dimensional representation of the quaternion time in the receiver reference frame in Figure 2.
Therefore, we can summarize the time at a distance expressions in the transmitter and receiver coordinate systems respectively,
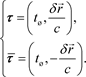(3)
Using postulates of time algebra [1] , we define the measured time-of-flight interval as the absolute value of the quaternion time interval. Then, from (1) and (2),
(4)
Note that the absolute value of the time interval at a distance is symmetric and independent of the choice of the coordinate system. Thus, the measured value of the time delay between the electromagnetic signal emission and signal detection is described by a scalar interval equal to the length of the quaternion time-of-flight. However, we always assume that the measured time-of-flight is positive in the direction from the transmitter to the receiver.
To clarify the experimental procedure, let us consider a clock on the kitchen wall and an imaging camera with a built-in clock that can time-stamp the images.
![]()
Figure 2. Time delay of an electromagnetic signal propagation from a distant transmitter to a receiver at the origin, as a function of the three-dimensional distance, 
, in the laboratory reference frame.
First, we bring the camera to the location of the kitchen clock, where we synchronize the two clocks. Next, we bring the camera some distance away, for example about three meters from the kitchen clock, 
, and take a picture of the kitchen clock from that distance. We can describe the same experiment in either the transmitter reference system of the kitchen clock or the receiver reference frame of the imaging camera resulting in the quaternion time expressions of (3). Thus, based on (4), we will observe a real scalar difference of about,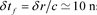 
between the time-stamp of the picture and the time shown on the clock in the image. Importantly, the time in the image, which corresponds to the emission time, is earlier than the time of the time-stamp, which corresponds to the time of signal detection. Consequently, the measured time interval is always positive from the transmitter to the receiver, as expected from (3) and (4).
In the presence of relative motion between the transmitter and receiver, we can define the quaternion time interval and its conjugate using the vector velocity [1] ,
![]()
(5)
Here we defined the relative vector velocity as,
![]()
(6)
Then, the measured time of flight interval becomes velocity and time dependent,
![]()
(7)
Now, we can calculate the measured the time interval at a distance, ![]()
, relative to the time interval at the origin, ![]()
,
![]()
(8)
This leads to a scalar relation for the time interval at a distance in the presence of motion,
![]()
(9)
which we recognize as the Lorentz time dilation formula. It has been shown [1] that (9) leads to the optical Doppler effect analysis initiated by [3] and experimentally verified by Ives and Stilwell [4] [5] .
3. Quaternion Frequency and Energy
Let us assume that the electromagnetic interaction can be represented by a monochromatic wave with angular frequency, ![]()
, where the period of oscillations is equal to the quaternion time interval,![]()
.
Subsequently, for electromagnetic waves, we can define the quaternion frequency [1] and its conjugate as,
![]()
(10)
Note that owing to the properties of quaternion division, we observe a sign change in the vector part of the quaternion frequency. The normal quaternion corresponds to the frequency in the receiver coordinate system, whereas the conjugate representation corresponds to the frequency in the transmitter coordinate system.
By using wave and particle duality, we introduce the quaternion energy of a free wave and express it using correspondence as the quaternion mass, ![]()
, of a free particle,
![]()
(11)
where, ![]()
, is Planck’s constant and, ![]()
, is a vector momentum.
Thus, we obtained a quaternion description of the inertial particle motion in the transmitter and receiver coordinate systems.
The measured inertial energy is again given by the absolute value of the quaternion energy [1] resulting in the well known expression,
![]()
(12)
Note that the measured energy is symmetric with respect to the quaternion and its conjugate and consequently does not depend on the choice of the coordinate system.
Next, let us assume that the external electromagnetic interaction can be expressed using a quaternion electromagnetic potential, ![]()
, similar to the four-potential of the traditional electromagnetic theory. Then, we express the total quaternion energy, including the energy of the free particle motion together with the external electromagnetic interaction, in the receiver and transmitter coordinate systems as,
![]()
(13)
where, q, is the elementary particle charge representing a scale parameter of the electromagnetic interactions and consequently becoming a key physical parameter of electromagnetic theory. Note that we preserved the sign convention in (13), whereas the normal quaternion expression corresponds to the potential in the receiver coordinate system while the conjugate expression corresponds to the potential in the transmitter coordinate system.
Again, we can easily obtain the measured value of the total particle energy as the square of the Euclidean norm of the total energy [1] ,
![]()
(14)
In the presence of external electromagnetic interactions, the applied energy is generally a function of the quaternion time whereas the free particle energy is a constant. Therefore, we assume that the total quaternion energy is generally time dependent via the external energy.
To account for both energy and time, we introduced [1] an eight-dimensional octonion configuration manifold, which we call the Olam (Hebrew for the World), ![]()
, where the quaternion time, ![]()
, is the main independent attribute and the quaternion energy, ![]()
, is the main time dependent dynamic attribute, which is orthogonal to the quaternion time. We can express the Olam configuration manifold in the receiver and transmitter coordinate systems using the Cayley-Dikson construction,
![]()
(15)
Therefore, we were able to express the total energy, including the free particle energy and energy of the external electromagnetic interaction, as an octonion configuration manifold in the receiver and transmitter coordinate systems.
Let us assume that all the dynamic properties of a physical system are determined using variations in the quaternion energy with quaternion time.
Therefore, we need to introduce a viable quaternion calculus using the properties of quaternion division algebra to account for variations of the quaternion energy with quaternion time.
4. Quaternion Time Path Derivative
A frequently used quaternion derivative was introduced by Fueter [38] [39] using a quaternion version of the Cauchy-Riemann condition. Similarly, a quaternion gradient, its conjugate, and Laplace operators were proposed by Devours [29] , who attempted to derive Maxwell’s equations using the quaternion approach.
By contrast, we propose defining a quaternion gradient operator along the quaternion path interval, whereas the components of the derivative’s nominator and denominator are interrelated by the path interval rather than by the Cauchy-Riemann condition. This allows for a simpler and more intuitive definition of the derivative.
Let us consider the quaternion function of the quaternion time, ![]()
, along a quaternion time path in the quaternion time manifold.
Let us assume that the quaternion time path [1] , is a sequence of connected quaternion time intervals from the source point, ![]()
, to the final destination time point,![]()
.
![]()
(16)
Here, we assume that the time path can be broken into, N, discrete quaternion time intervals, as shown in Figure 3. Note that the total sum is not dependent on the actual time intervals but is a function of only the initial and final quaternion time points.
The measured length of the quaternion time path, ![]()
, is equal to the sum of the individual measured quaternion time intervals, ![]()
, along the time path from the source-point to the destination-point.
![]()
(17)
Therefore, the total measured time path depends on the path [1] .
Assume that the quaternion function, ![]()
, can be broken into corresponding intervals, ![]()
, along the time path,
![]()
(18)
Next we define an infinitesimal quaternion time interval,
![]()
(19)
where, the time interval has an infinitesimal length,
![]()
(20)
We define the differential interval of a quaternion function, ![]()
, which corresponds to the differential time interval, ![]()
, as,
![]()
(21)
Next, we use quaternion division to define a proper quaternion path derivative,
![]()
Figure 3. Multiple paths arriving at the same quaternion time point may result in different measured times.
noting that because of the non-commutative nature of quaternion division, we need to define both the right and left derivatives. Therefore, we define the right derivative as,
![]()
(22)
Similarly, the left quaternion path derivative is defined as,
![]()
(23)
Consequently, the quaternion path derivative can be defined for any quaternion function of a quaternion time interval, as long as the operation of division is valid and the absolute value of the time interval is not equal to zero,![]()
.
We define a quaternion path gradient operator using the definition of the quaternion multiplicative inverse,
![]()
(24)
Next, we use the condition of partial differentiation to simplify Equation (24). For example, we calculate the scalar part as, ![]()
, assuming that, ![]()
, while, ![]()
, ![]()
,![]()
. This leads from (24) to,
![]()
(25)
Using a similar calculation for all partial derivatives, we obtain a quaternion version of the total time gradient operator along the path in terms of partial derivatives,
![]()
(26)
Therefore, using quaternion division, we defined a mathematically consistent version of the path gradient which is a quaternion conjugate of the traditional gradient [38] [39] because of the properties of quaternion division. The conjugate quaternion representation of the normal quaternion gradient operator is critical to our theory.
Similarly, we can define a conjugate quaternion gradient operator over the path,
![]()
(27)
Using the definitions of the right and left derivatives (22) and (23), we express the quaternion path derivative of a quaternion function as a function multiplied by a conjugate gradient operator as follows,
![]()
(28)
The conjugate path derivative of a quaternion function is then given by the conjugate function multiplied by a normal quaternion gradient expression,
![]()
(29)
We use a quaternion multiplication formula, which can be expressed in terms of vector and scalar quantities using the Heaviside-Gibbs vector notation for any two quaternions, ![]()
and![]()
,
![]()
(30)
Using (28) and (30), we derive a complete quaternion derivative represented in the vector notation,
![]()
(31)
Similarly using (29) and (30), we derive the quaternion conjugate derivative,
![]()
(32)
Next, we define the quaternion Laplacian operator multiplying the quaternion derivative by its conjugate [29] ,
![]()
(33)
Note that the quaternion Laplacian operator can be considered a scalar operator and consequently commutes with the quaternion function. We express the quaternion Laplacian operator in terms of partial derivatives as,
![]()
(34)
Thus, the Laplacian operator has the same form for the left and right derivatives as well as for the regular and conjugate quaternion functions.
Note that we can use a similar procedure to define derivatives of a complex function, ![]()
, which depends on a complex variable![]()
, as complex numbers also belong to a set of normed division algebras. Because complex numbers are commutative, we have only one of each normal and conjugate derivatives,
![]()
(35)
Note that the complex path derivative is different from the traditional complex derivative and should be valid for any complex function and complex time interval where the absolute value of the time interval is not equal to zero,![]()
. Therefore, the Cauchy-Riemann condition is not required for either the complex or quaternion path derivatives.
Similar to the quaternion Laplacian operator, we can define a complex Laplacian,
![]()
(36)
Thus, we defined a complete set of normal and conjugate derivatives for both the complex and quaternion functions.
5. Application of Quaternion Differentiation to Electromagnetic Potentials
Assume that the total energy of the particle changes along the time path under the influence of an external interaction, as given by (13).
Using the quaternion time-path derivative, we develop a quaternion electromagnetic equations using a modified version of the quaternion electromagnetic potential function,![]()
. Then, we express the externally applied electromagnetic energy in the transmitter and receiver coordinate systems respectively,
![]()
(37)
This allows us to develop electromagnetic equations using quaternion time differentiation rather than traditional space differentiation. We use the definitions of the conjugate and normal quaternion gradient operators, which correspond to the time path gradients in the transmitter and receiver coordinate systems, respectively,
![]()
(38)
According to Newton’s Second Law, the force is defined as,![]()
. Note that based on the definition (37) of the potential function, ![]()
, has units of the momentum. Therefore, we define the quaternion electromagnetic force in terms of the derivatives of the quaternion potential, which in the receiver reference frame becomes,
![]()
(39)
which we identify as the quaternion form of the Lorentz electromagnetic force equations expressed in terms of the applied potentials. Similarly, we can define the electromagnetic force in the transmitter reference frame as,
![]()
(40)
The Laplacian operator has the same form for the left and right derivatives as well as for the regular and conjugate potential functions. This property seems extremely suggestive, as we can now define the quaternion current density in terms of the quaternion applied potential, by correspondence with the conventional Poisson’s equation [16] ,
![]()
(41)
where we define the scalar part of the quaternion current density as the scalar charge density multiplied by the saturation velocity, ![]()
, while the vector part is the vector current density,![]()
.
Therefore, the quaternion current density can be readily expressed in terms of the applied scalar and vector potentials,
![]()
(42)
We succeeded in expressing the scalar charge density and vector current density in terms of the scalar and vector applied potentials,
![]()
(43)
The resulting equations represent electromagnetic interactions and electromagnetic matter in terms of the applied quaternion potential. Because the resulting equations are in Laplacian form, they automatically represent wave equations for the potentials and consequently lead to the electromagnetic potential waves.
6. Application of Quaternion Differentiation to Electromagnetic Fields
Next, we use quaternion electromagnetic potentials and forces to define the electromagnetic fields, which allows us to derive electromagnetic equations in a more familiar three dimensional field form of the conventional Maxwell equations.
To do so, we apply the multiplication formula to the quaternion applied potential and gradient operators in the receiver reference frame,
![]()
(44)
resulting in the following form of the quaternion derivative in terms of vector relations,
![]()
(45)
Note that using quaternion multiplication, we conclude that the vector gradient operator, ![]()
, and the divergence operator, ![]()
, are commutative. On the other hand, the vector curl operator, ![]()
, is anti-commutative.
Let us define the quaternion electric field, ![]()
, and the quaternion magnetic field, ![]()
, as the anti-commutator and commutator expressions of the derivative [30] ,
![]()
(46)
Using the left and right differentiation of the external potential, we define the electromagnetic force in terms of the quaternion electric and magnetic fields as follows,
![]()
(47)
where we determine the scalar and vector components of the fields from (45) and (46),
![]()
(48)
We note that the vector electric, ![]()
, and the vector magnetic, ![]()
fields, defined here (48) are similar to the modern definitions [13] [14] . However, we note in (48) the existence of a scalar electric field, ![]()
, which is absent in Maxwell’s equations. Jack [30] suggested that the scalar electric field describes thermal electricity. On the other hand, the quaternion magnetic field is represented by a pure vector quantity, ![]()
, similar to the traditional expression.
Note that the resulting force expressions (47) have correct dimensions based on our definitions of the electric and magnetic fields (48), unlike the traditional empirical expression, which includes a vector velocity in front of the magnetic field [13] . The force equations (47) indicate the existence of two types of charges that behave differently in the magnetic field, while we did not use the carrier velocity to define the two types of charges. It seems that the two Lorentz force field expressions (47), obtained analytically from basic mathematical principles, properly describe the forces on charged particles without the need to use the empirical particle velocity.
Next, we apply the conjugate quaternion gradient operator to obtain the quaternion Laplacian in terms of electromagnetic fields. As mentioned previously, we used the quaternion current density definition (42) to derive the following two expressions for electromagnetic currents,
![]()
(49)
Using quaternion multiplication in (49) we finally obtain,
![]()
(50)
Despite the apparent difference between the two Laplacian expressions in (50), they must yield the same result because of the commutative property of the quaternion Laplacian, which lead to the following result for the quaternion current density,
![]()
(51)
The above derivation uses the following vector relation for the electromagnetic fields,
![]()
(52)
which we immediately recognize as Faraday’s law of Maxwell’s equations [13] [14] , which we derive from purely mathematical properties of the quaternion calculus. In addition, we used the following vector identity in (50),
![]()
(53)
Therefore, we can express the scalar charge density and vector current density in terms of the electromagnetic fields as,
![]()
(54)
In addition to the static traditional charge density given by the divergence of the vector electric field,
![]()
(55)
we can identify a time-dependent component of charge density, which by comparison with the time dependent semiconductor charge density we recognize as the generation-recombination charge,
![]()
(56)
The vector current density in (54) can be expressed in terms of various components, similar to the original Maxwell equations,
![]()
(57)
where,
![]()
(58)
we identify as the time dependent displacement current. The magnetic current density we identify as,
![]()
(59)
Finally, we introduce the conduction current component,
![]()
(60)
which we identify as the new form of Ohm’s law for the conduction current. Note that our form of Ohm’s resembles Shockley’s version of the conduction current in semiconductors,
![]()
(61)
where, ![]()
, is the semiconductor charge density, ![]()
, is the carrier mobility, and, ![]()
, is the quasi Fermi potential.
We believe that our analytical definition of Ohm’s law is advantageous because it was derived purely analytically from the basic mathematical properties of quaternion mathematics. Note that the scalar electric field is responsible for both the generation-recombination charge density and the new form of Ohm’s law.
Note that in the original Maxwell equations [9] , Ohm’s law is defined empirically as,
![]()
(62)
where, ![]()
, is the empirical electrical conductivity. Surprisingly, Ohm’s law does not appear in Heaviside’s version of electromagnetic equations [12] , where the total current is written without the conduction component,
![]()
(63)
Furthermore, the sign of the displacement current, ![]()
, is different in the modified equations, which seems to be a misrepresentation of the original form of Maxwell’s equations. The particular choice of displacement current is essential for Heaviside’s version, as it leads to electromagnetic wave equations in terms of the electric and magnetic fields [12] . Maxwell [9] expressed the magnetic and electric currents separately, corresponding to the presence of either the magnetic or electric field. When both electric and magnetic fields are present, the identification and separation of the current components in (57) becomes complicated by the interrelation between the vector and scalar fields in terms of the more fundamental potentials (48).
Therefore, it seems that the new analytical formulation of the quaternion form of Maxwell’s equation helped us detect an error in the widely used modified version of the electromagnetic equations [13] [14] , which is a modified version of the original Maxwell equations [9] .
Therefore, we can summarize the new quaternion version of the electromagnetic equations in the receiver reference frame in terms of both potentials and fields as follows,
![]()
(64)
The set of equations is completed by a supplementary vector relationship between the electric and magnetic fields, which is equivalent to Faraday’s law,
![]()
(65)
which together with the definition of the fields in terms of potentials (48) create a non-trivial relation between the electric and magnetic fields. This is not desirable for any electromagnetic theory as it interferes with the clear identification of the electromagnetic currents and waves. Therefore, it seems advantageous to express the theory in terms of potentials only, where we can treat the scalar potential, ![]()
, and vector potential, ![]()
, as truly independent quantities. Consequently, it seems preferable to use the electromagnetic matter equations in terms of potentials, as we obtained here using the quaternion gradient (40) and Laplacian (41) operators. This is consistent with results of Aharonov and Bohm [32] .
7. Postulates and Equations of Time and Matter
Thus, based on the previous work previous work [1] and the current study, we can formulate the main postulates and equations of electromagnetic matter. First, we express all the equation in the receiver frame of reference, where the time of signal emission is given by the quaternion time at a distance.
Postulate 1 (Euclidean Division Algebras). Division algebras with Euclidean norm, consisting of real numbers, complex numbers, real quaternions, and octonions, are essential mathematical tools of nature. Any measurement by an apparatus located at the origin of a coordinate system is given by a real scalar number. Furthermore, any measurement at a distance of a physical quantity at a distance from the origin is given by a real scalar absolute value, which is its Euclidean norm,
![]()
(66)
Postulate 2 (Quaternion Time at a Distance). There is a maximum speed of any signal propagation, which is identified in a vacuum with the speed of light, c. Because of the maximum speed, there is a positive propagation delay, which is represented by a vector time of flight,![]()
. Then, the time of signal emission at a distance from the origin in the receiver reference frame is given by the conjugate quaternion expression,
![]()
(67)
Postulate 3 (Quaternion Total Energy). During arbitrary motion under the influence of an external interaction, including propagation and rotation, we must consider the three-dimensional nature of space and momentum. Therefore, the energy of arbitrary motion is given by the quaternion energy including the quaternion potential of the external electromagnetic interaction,
![]()
(68)
The quaternion time and time-dependent quaternion energy form an orthogonal eight-dimensional octonion manifold that fully describes the the natural world. The octonion configuration manifold can be represented as two orthogonal quaternions using the Cayley-Dikson construct,
![]()
(69)
Postulate 4 (First Quaternion Derivatives—Force Fields). The dynamic properties of natural phenomena are given by variations in the quaternion energy with quaternion time. The quaternion path derivative is defined using the properties of quaternion division. The first quaternion derivative of the external quaternion potential with respect to time is proportional to the force produced by external interactions. We can write the force in terms of quaternion derivatives as,
![]()
(70)
The force fields include scalar and collinear electric fields, and rotational magnetic field components.
Postulate 5 (Second Quaternion Derivative—Matter Current). The second derivative of the quaternion energy with respect to time, given by a quaternion Laplacian operator, is proportional to the electromagnetic matter current, which includes scalar matter density and three-dimensional vector current,
![]()
(71)
This can be considered a generalized quaternion version of Maxwell’s current equations.
Postulate 6 (Conjugate Quaternions—Transmitter and Receiver Frames). All the physical quantities in the transmitter reference frame assume a quaternion conjugate representation of the corresponding mathematical expressions in the receiver reference frame. The process of conjugation is a mathematical involution that does not carry new information for the absolute values of the measured physical quantities, which are the same in the receiver and transmitter reference frames. However, imaginary vector quantities, such as vector force fields and currents, assume opposite directions owing to conjugation.
It can be easily shown that the electromagnetic equations in the transmitter frame of reference become,
![]()
(72)
Note that the present electromagnetic equations include a formulation of time at a distance and consequently account for the retarded potentials of the action at a distance.
8. Conclusions
We demonstrated an analytic derivation of electromagnetic matter equations using the theory of quaternion time and applying it to electromagnetic interactions. We assumed the existence of a time delay between the emission of the electromagnetic signal detection due to the final speed of signal propagation. We introduced the transmitter and receiver coordinate systems to describe the interaction and showed that the resulting quaternion expressions are conjugates of each other.
Then, we proposed a quaternion path derivative using the division properties of quaternions. We defined the gradient operator as the multiplicative inverse of the quaternion time. We applied the quaternion gradient and Laplacian operators to the quaternion electromagnetic potential to derive the quaternion form of Maxwell’s equations.
This resulted in a new definition of electromagnetic force, which led to a scalar electric field. We demonstrated that the scalar electric field is responsible for the additional effects appearing in the electromagnetic equations, which can be interpreted as the generation-recombination charge density and a new form of Ohm’s law for the conduction current density. Crucially, we demonstrated the electromagnetic equations using equivalent quaternion potential and field equations. It appears that the potential formulation is preferable because it lacks the complex interdependence of the electric and magnetic fields.
We showed that the quaternion sets of the time and matter equations in the transmitter reference are quaternion conjugates of the same equations in the receiver reference frame. Therefore, the new theory of electromagnetic matter based on normed division algebras appears to be highly comprehensive, logical, and compelling.
Acknowledgements
I thank Prof. Leon Altschul, Victor E. Matizen, and Prof. Jeremy Dunning-Davies for their helpful discussions. I thank Prof. Alan J. Oppenheim and Ray Stata for continuous encouragement of this research. Many thanks to Gennady Fiksman, Valery Garber, and Heidi Brun for their detailed reviews.