Finite Time Domain Dynamics of Dirac Fields

Emmanouil George Thrapsaniotis

Athens, Greece.

DOI: 10.4236/jamp.2023.1112250                

Abstract

In the present paper we consider the case of a Dirac field in a finite time domain and coupled to an external field. We decompose the field and its Hamiltonian in terms of creation and annihilation operators and path integrate it via Grassmannian variables techniques. In that way we obtain its finite time domain Green function. We use it in the perturbative study of the interaction of Dirac particles with classical electromagnetic waves.

Keywords

Dirac Fields, Finite Time Domain, Time Propagation, Electromagnetic Wave, Perturbation Theory

1. Introduction

Quantum field theory is an important area of physics with various applications [1] [2] [3] [4] . It studies the dynamics of particles of various characteristics including spin, charge and mass.

In the present paper, we intend to give techniques for the study of finite time evolution within quantum field theory (See [5] for earlier attempts). More particularly we consider the case of finite time domain Dirac fields [6] - [11] evolution and study them via path integral methods. We begin from their standard Lagrangian and Hamiltonian densities, expand the fields in terms of anticommuting creation and annihilation operators and path integrate the corresponding Hamiltonian via standard Grassmannian variables techniques [12] . So, on considering vacuum to vacuum transitions we derive the corresponding Green function. It gives the whole dynamical information of the physical system. We use it in the study of Dirac particles’ interaction with an external field [6] [7] [8] , specifically a classical electromagnetic wave. We use perturbative methods with respect to the electromagnetic field and keep first-order terms. From the derived expressions we can study the time evolution of the distribution in space of quantities such as the probability density and therefore of the possible motion of the particles. More particularly here we derive for certain times contour plots of the probability density of a particle initially at rest which has a Gaussian spinor form. We observe that due to the interaction the particle’s probability density spreads and the particle moves away from its initial position.

The present paper proceeds as follows. In section 2 we give the present Dirac field system, expand the field in terms of anticommuting creation and annihilation operators and path integrate the Hamiltonian within a finite time domain to extract the transition amplitude between Grassmann states and more particularly between vacuum states. Then in section 3, we use that result to obtain the Green function. In section 4 we use that Green function in order to perturbatively extract the time evolution of the probability density of a Gaussian Dirac particle interacting with an electromagnetic wave and give appropriate contour plots. Finally, in section 5, we give our conclusions.

In the present paper we set $c=\hslash =1$ . Then $e^2=\alpha \simeq \frac{1}{137}$ , where $\alpha$ is the

fine structure constant. Below we maintain the mass symbol m for clarity and finally in our calculations we set $m=1$ as well. The electron rest energy is $m{c}^2$ while the Rydberg energy has value $m{c}^2{\alpha }^2/2$ . The atomic units of length, time

and energy are $\frac{{\hslash }^2}{m{e}^2}$ , $\frac{{\hslash }^3}{m{e}^4}$ and $\frac{m{e}^4}{{\hslash }^2}$ respectively.

2. System and Path Integration

We consider a Dirac field $\Psi$ of mass m coupled to a current X. Its Lagrangian is

$L=\bar{\Psi }\left(i{\gamma }^{\mu }{\partial }_{\mu }-m\right)\Psi +\bar{X}\Psi +\bar{\Psi }X$ (1)

and its corresponding classical action

$I_0\left(\Psi ,X\right)={\displaystyle \int \text{d}\tau }{\displaystyle \int {\text{d}}^{3}x\left[\bar{\Psi }\left(i{\gamma }^{\mu }{\partial }_{\mu }-m\right)\Psi +\bar{X}\Psi +\bar{\Psi }X\right]}$ (2)

${\gamma }^{\mu }$ are Dirac matrices and $\bar{\Psi }={\Psi }^{+}\beta ={\Psi }^{+}{\gamma }^0$ .

We introduce the current in order to use standard properties of the Green function and obtain it after integrating the whole system (see Equation (55) below).

So according to variational considerations, the free field $\Psi$ obeys the equation

$\left(i{\gamma }^{\mu }{\partial }_{\mu }-m\right)\Psi =0$ (3)

called the Dirac equation.

The momentum canonically conjugate to the spinor field has the form

$\pi =\frac{\partial L}{\partial \stackrel{\dot{}}{\Psi }}=i{\Psi }^{+}$ (4)

and the quantum Hamiltonian is given as

$H={\displaystyle \int {\text{d}}^{3}x}\left[\pi \stackrel{\dot{}}{\Psi }-L\right]={\displaystyle \int {\text{d}}^{3}x}\left[{\Psi }^{+}\left(-i\stackrel{\to }{\alpha }\cdot \stackrel{\to }{\nabla }+\beta m\right)\Psi -\bar{X}\Psi -\bar{\Psi }X\right]$ . (5)

Here we study fermions. So $\Psi$ and ${\Psi }^{+}$ must satisfy equal time anticommutation relations,

$\left\{{\Psi }_{\alpha }\left(\stackrel{\to }{x},t\right),{\Psi }_{\beta }^{+}\left(\stackrel{\to }{y},t\right)\right\}={\delta }_{\alpha \beta }{\delta }^3\left(\stackrel{\to }{x}-\stackrel{\to }{y}\right)$ (6)

$\left\{{\Psi }_{\alpha }\left(\stackrel{\to }{x},t\right),{\Psi }_{\beta }\left(\stackrel{\to }{y},t\right)\right\}=\left\{{\Psi }_{\alpha }^{+}\left(\stackrel{\to }{x},t\right),{\Psi }_{\beta }^{+}\left(\stackrel{\to }{y},t\right)\right\}=0$ . (7)

We expand the fields in creation and annihilation operator components

${\Psi }_{\alpha }\left(\stackrel{\to }{x},t\right)={\displaystyle \underset{r=1}{\overset{4}{\sum }}{\displaystyle \int \frac{{\text{d}}^{3}p}{{\left(2\pi \right)}^3}}}\frac{m}{E_{\stackrel{\to }{p}}}b\left(\stackrel{\to }{p},r,t\right)w_{\alpha }\left(\stackrel{\to }{p},r\right){\text{e}}^{i\stackrel{\to }{p}\cdot \stackrel{\to }{x}}$ (8)

${\Psi }_{\alpha }^{+}\left(\stackrel{\to }{x},t\right)={\displaystyle \underset{r=1}{\overset{4}{\sum }}{\displaystyle \int \frac{{\text{d}}^{3}p}{{\left(2\pi \right)}^3}}}\frac{m}{E_{\stackrel{\to }{p}}}{b}^{+}\left(\stackrel{\to }{p},r,t\right)w_{\alpha }^{+}\left(\stackrel{\to }{p},r\right){\text{e}}^{-i\stackrel{\to }{p}\cdot \stackrel{\to }{x}}$ (9)

and let the sources have the form

$X\left(\stackrel{\to }{x},t\right)={\displaystyle \underset{r=1}{\overset{4}{\sum }}{\displaystyle \int \frac{{\text{d}}^{3}p}{{\left(2\pi \right)}^3}}}\frac{m}{E_{\stackrel{\to }{p}}}\chi \left(\stackrel{\to }{p},r,t\right)w\left(\stackrel{\to }{p},r\right){\text{e}}^{i\stackrel{\to }{p}\cdot \stackrel{\to }{x}}$ (10)

$\bar{X}\left(\stackrel{\to }{x},t\right)={\displaystyle \underset{r=1}{\overset{4}{\sum }}{\displaystyle \int \frac{{\text{d}}^{3}p}{{\left(2\pi \right)}^3}}}\frac{m}{E_{\stackrel{\to }{p}}}{\chi }^{\ast }\left(\stackrel{\to }{p},r,t\right)\bar{w}\left(\stackrel{\to }{p},r\right){\text{e}}^{-i\stackrel{\to }{p}\cdot \stackrel{\to }{x}}$ . (11)

We have set

$E_{\stackrel{\to }{p}}=\sqrt{m^2+{\stackrel{\to }{p}}^2}$ (12)

$w\left(\stackrel{\to }{p},1\right)=\sqrt{\frac{E_{\stackrel{\to }{p}}+m}{2m}}\left(\begin{array}{c}1\\ 0\\ \frac{p_z}{E_{\stackrel{\to }{p}}+m}\\ \frac{p_{+}}{E_{\stackrel{\to }{p}}+m}\end{array}\right)$ (13)

$w\left(\stackrel{\to }{p},2\right)=\sqrt{\frac{E_{\stackrel{\to }{p}}+m}{2m}}\left(\begin{array}{c}0\\ 1\\ \frac{p_{-}}{E_{\stackrel{\to }{p}}+m}\\ \frac{-p_z}{E_{\stackrel{\to }{p}}+m}\end{array}\right)$ (14)

$w\left(\stackrel{\to }{p},3\right)=\sqrt{\frac{E_{\stackrel{\to }{p}}+m}{2m}}\left(\begin{array}{c}\frac{-p_z}{E_{\stackrel{\to }{p}}+m}\\ \frac{-p_{+}}{E_{\stackrel{\to }{p}}+m}\\ 1\\ 0\end{array}\right)$ (15)

and

$w\left(\stackrel{\to }{p},4\right)=\sqrt{\frac{E_{\stackrel{\to }{p}}+m}{2m}}\left(\begin{array}{c}\frac{-p_{-}}{E_{\stackrel{\to }{p}}+m}\\ \frac{p_z}{E_{\stackrel{\to }{p}}+m}\\ 0\\ 1\end{array}\right)$ (16)

where $p_{\pm }=p_x\pm i{p}_y$ .

The spinors satisfy the following orthogonality and completeness relations

$w^{+}\left(\stackrel{\to }{p},r\right)w\left(\stackrel{\to }{p},r^{\prime }\right)=\frac{E_{\stackrel{\to }{p}}}{m}{\delta }_{r{r}^{\prime }}$ (17)

$\bar{w}\left({\epsilon }_r\stackrel{\to }{p},r\right)w\left({\epsilon }_{r^{\prime }}\stackrel{\to }{p},r^{\prime }\right)={\epsilon }_r{\delta }_{r{r}^{\prime }}$ (18)

${\displaystyle \underset{r=1}{\overset{4}{\sum }}{w}_{\alpha }\left(\stackrel{\to }{p},r\right)w_{\beta }^{+}\left(\stackrel{\to }{p},r\right)}=\frac{E_{\stackrel{\to }{p}}}{m}{\delta }_{\alpha \beta }$ (19)

where ${\epsilon }_r=1$ for $r=1,2$ and ${\epsilon }_r=-1$ for $r=3,4$ .

In order ${\Psi }_{\alpha }\left(\stackrel{\to }{x}\right)$ and ${\Psi }_{\beta }^{+}\left(\stackrel{\to }{x}\right)$ to satisfy the anticommutation relations (6, 7), $b$ and $b^{+}$ must satisfy

$\left\{b\left(\stackrel{\to }{p},r\right),b^{+}\left({\stackrel{\to }{p}}^{\prime },r^{\prime }\right)\right\}={\left(2\pi \right)}^3\frac{E_{\stackrel{\to }{p}}}{m}{\delta }_{r{r}^{\prime }}{\delta }^3\left(\stackrel{\to }{p}-{\stackrel{\to }{p}}^{\prime }\right)$ (20)

$\left\{b\left(\stackrel{\to }{p},r\right),b\left({\stackrel{\to }{p}}^{\prime },r^{\prime }\right)\right\}=\left\{b^{+}\left(\stackrel{\to }{p},r\right),b^{+}\left({\stackrel{\to }{p}}^{\prime },r^{\prime }\right)\right\}=0$ . (21)

Now, on using the above information the Hamiltonian (5) takes the following form

$H={\displaystyle \underset{r=1}{\overset{4}{\sum }}{\displaystyle \int \frac{{\text{d}}^{3}p}{{\left(2\pi \right)}^3}}}\frac{m}{E_{\stackrel{\to }{p}}}{\epsilon }_r\left[E_{\stackrel{\to }{p}}{b}^{+}\left(\stackrel{\to }{p},r\right)b\left(\stackrel{\to }{p},r\right)-\frac{m}{E_{\stackrel{\to }{p}}}\left(\chi \left(\stackrel{\to }{p},r,t\right)b^{+}\left(\stackrel{\to }{p},r\right)+{\chi }^{\ast }\left(\stackrel{\to }{p},r,t\right)b\left(\stackrel{\to }{p},r\right)\right)\right]$ . (22)

We observe that it constitutes of the sum of single mode Hamiltonians of the form

$H_0=E{b}^{+}b-\frac{m}{E}\left(\chi b^{+}+{\chi }^{\ast }b\right)$ (23)

where $b$ and $b^{+}$ are annihilation and creation operators for fermions which satisfy the anticommutation relations (20, 21). They are a reflection of the Pauli principle. We intend to evaluate the propagator. Initially we consider the free case with the following Hamiltonian for one fermion

$H_1=E{b}^{+}b$ (24)

We intend to construct a path integral representation of the evolution operator $U_1\left(t\right)={\text{e}}^{-i{H}_{1}t}$ . To proceed we introduce Grassmann variables $\xi$ , $\bar{\xi }$ within a Grassmann algebra $\Im$ and represent the Hamiltonian operator $H_1$ as an operator acting on functions defined on that Grassmann algebra $\Im$ . Then

$H_1=E\bar{\xi }\frac{\partial }{\partial \bar{\xi }}$ , $\bar{\xi }\in \Im$ . (25)

Functions of $\bar{\xi }$ constitute a vector space of dimension two.

What motivates to use Grassmann variables is the fact that they obey a similar algebraic structure with the anticommutation structure obeyed by the Fermionic operators $b^{+}$ and $b$ . So, we proceed via standard path integral techniques [1] [12] . At first, we suppose that t is small and get

$\langle \bar{\xi }|U_1\left(t\right)|{\xi }^{\prime }\rangle =\left[1-itE\bar{\xi }\frac{\partial }{\partial \bar{\xi }}+O\left(t^2\right)\right]{\text{e}}^{-\bar{\xi }{\xi }^{\prime }}={\text{e}}^{-\bar{\xi }{\xi }^{\prime }\left(1-iEt\right)}+O\left(t^2\right)$ . (26)

Then we use the group property

${\displaystyle \int \text{d}{\xi }^{″}\text{d}{\bar{\xi }}^{″}\langle \bar{\xi }|U_2|{\xi }^{″}\rangle {\text{e}}^{{\bar{\xi }}^{″}{\xi }^{″}}\langle {\bar{\xi }}^{″}|U_1|{\xi }^{\prime }\rangle }=\langle \bar{\xi }|U_2{U}_1|{\xi }^{\prime }\rangle$ (27)

to write the evolution operator at finite time

$\langle {\bar{\xi }}_f|U_1\left(t_f,t_i\right)|{\xi }_i\rangle =\underset{n\to \infty }{\lim }{\displaystyle \int {\displaystyle \underset{k=1}{\overset{n-1}{\prod }}\text{d}{\xi }_k\text{d}{\bar{\xi }}_k}}\exp \left[i{S}_1\left({\bar{\xi }}_k,{\xi }_k\right)\right]$ (28)

where

$S_1\left({\bar{\xi }}_k,{\xi }_k\right)=i{\displaystyle \underset{k=1}{\overset{n-1}{\sum }}{\bar{\xi }}_k\left({\xi }_k-{\xi }_{k-1}\right)+i{\bar{\xi }}_n{\xi }_{n-1}-E\epsilon {\displaystyle \underset{k=1}{\overset{n}{\sum }}{\bar{\xi }}_k{\xi }_{k-1}}}$ (29)

$\epsilon =\frac{t_f-t_i}{n}$ (30)

and

${\xi }_0={\xi }_i,{\bar{\xi }}_n={\bar{\xi }}_f$ . (31)

In the large n limit we obtain the path integral representation for the matrix elements of $U_1\left(t_f,t_i\right)$

$\langle {\bar{\xi }}_f|U_1\left(t_f,t_i\right)|{\xi }_i\rangle ={\displaystyle \underset{\xi \left(t_i\right)={\xi }_i}{\overset{\bar{\xi }\left(t_f\right)={\bar{\xi }}_f}{\int }}D\xi }\left(t\right)D\bar{\xi }\left(t\right)\exp \left[i{S}_1\left(\bar{\xi },\xi \right)\right]$ (32)

with

$S_1\left(\bar{\xi },\xi \right)=-i\bar{\xi }\left(t_f\right)\xi \left(t_f\right)+{\displaystyle \underset{t_i}{\overset{t_f}{\int }}\text{d}t\bar{\xi }\left(t\right)\left[i\stackrel{\dot{}}{\xi }\left(t\right)-E\xi \left(t\right)\right]}$ . (33)

The above expressions immediately generalize to the case of the Hamiltonian (23). Then we obtain the path integral

$\langle {\bar{\xi }}_f|U_0\left(t_f,t_i\right)|{\xi }_i\rangle ={\displaystyle \underset{\xi \left(t_i\right)={\xi }_i}{\overset{\bar{\xi }\left(t_f\right)={\bar{\xi }}_f}{\int }}D\xi }\left(t\right)D\bar{\xi }\left(t\right)\exp \left[iS\left(\bar{\xi },\xi \right)\right]$ (34)

and the action

$\begin{array}{l}{S}_1\left(\bar{\xi },\xi \right)\\ =-i\bar{\xi }\left(t_f\right)\xi \left(t_f\right)+{\displaystyle \underset{t_i}{\overset{t_f}{\int }}\text{d}t\left\{\bar{\xi }\left(t\right)\left[i\stackrel{\dot{}}{\xi }\left(t\right)-E\xi \left(t\right)\right]+\frac{m}{E}\left(\chi \left(t\right)\bar{\xi }\left(t\right)+{\chi }^{\ast }\left(t\right)\xi \left(t\right)\right)\right\}}\end{array}$ (35)

where

$U_0\left(t_f,t_i\right)={\text{e}}^{-i{\displaystyle \underset{t_i}{\overset{t_f}{\int }}\text{d}t{H}_0\left(t\right)}}$ . (36)

The path integral (34) with action (35) is Gaussian and therefore it can be evaluated exactly. The saddle point equation obtained by varying $\bar{\xi }\left(t\right)$ yields

$i\stackrel{\dot{}}{\xi }-E\xi +\frac{m}{E}\chi =0$ (37)

with solution

$\xi \left(t\right)={\text{e}}^{-iE\left(t-t_i\right)}{\xi }_i+i\frac{m}{E}{\displaystyle \underset{t_i}{\overset{t}{\int }}\text{d}\tau }{\text{e}}^{-iE\left(t-\tau \right)}\chi \left(\tau \right)$ (38)

Similarly, the variation of $\xi \left(t\right)$ gives

$-i\stackrel{\dot{}}{\bar{\xi }}-E\bar{\xi }+\frac{m}{E}{\chi }^{\ast }=0$ (39)

with solution

$\bar{\xi }\left(t\right)={\text{e}}^{-iE\left(t_f-t\right)}{\bar{\xi }}_f+i\frac{m}{E}{\displaystyle \underset{t}{\overset{t_f}{\int }}\text{d}\tau {\text{e}}^{-iE\left(\tau -t\right)}}{\chi }^{\ast }\left(\tau \right)$ . (40)

In the above equations we have taken into account boundary conditions.

Finally, we restore the variables appearing in Equation (22) and perform standard manipulations within Equation (35) to obtain the propagator

$\begin{array}{l}{U}_0\left({\bar{\xi }}_f\left(\stackrel{\to }{p},r\right),t_f;{\xi }_i\left(\stackrel{\to }{p},r\right),t_i;X,\bar{X}\right)\\ =\exp \{{\bar{\xi }}_f\left(\stackrel{\to }{p},r\right){\text{e}}^{-i{E}_{\stackrel{\to }{p}}\left(t_f-t_i\right)}{\xi }_i\left(\stackrel{\to }{p},r\right)\begin{array}{c}\underset{}{}\\ \end{array}\\ +i\frac{m}{E_{\stackrel{\to }{p}}}{\displaystyle \underset{t_i}{\overset{t_f}{\int }}\text{d}t\left({\bar{\xi }}_f\left(\stackrel{\to }{p},r\right){\text{e}}^{-i{E}_{\stackrel{\to }{p}}\left(t_f-t\right)}\chi \left(\stackrel{\to }{p},r,t\right)+{\chi }^{\ast }\left(\stackrel{\to }{p},r,t\right){\text{e}}^{-i{E}_{\stackrel{\to }{p}}\left(t-t_i\right)}{\xi }_i\left(\stackrel{\to }{p},r\right)\right)}\\ -\frac{1}{2}{\left(\frac{m}{E_{\stackrel{\to }{p}}}\right)}^2{\displaystyle \underset{t_i}{\overset{t_f}{\int }}{\displaystyle \underset{t_i}{\overset{t_f}{\int }}\text{d}t}\text{d}{t}^{\prime }{\chi }^{\ast }\left(\stackrel{\to }{p},r,t\right){\text{e}}^{-i{E}_{\stackrel{\to }{p}}\left|t-t^{\prime }\right|}\chi \left(\stackrel{\to }{p},r,t^{\prime }\right)}\}\end{array}$ (41)

To derive that the normalization constant in Equation (41) is one we set $\chi ={\chi }^{\ast }=0$ and use the semigroup property.

In order to obtain the final form of the Grassmannian amplitude we have to integrate diagonally between the initial variable $\eta$ and the final one $\bar{\zeta }$. I.e.

$\begin{array}{l}U\left(\bar{\zeta }\left(\stackrel{\to }{p},r\right),t_f;\eta \left(\stackrel{\to }{p},r\right),t_i;X,\bar{X}\right)\\ ={\displaystyle \int \text{d}\xi \left(\stackrel{\to }{p},r\right)\text{d}\bar{\xi }\left(\stackrel{\to }{p},r\right){\text{e}}^{\bar{\xi }\left(\stackrel{\to }{p},r\right)\xi \left(\stackrel{\to }{p},r\right)}}\langle \bar{\zeta }\left(\stackrel{\to }{p},r\right)|\xi \left(\stackrel{\to }{p},r\right)\rangle \\ \times U_0\left(\bar{\xi }\left(\stackrel{\to }{p},r\right),t_f;\xi \left(\stackrel{\to }{p},r\right),t_i;X,\bar{X}\right)\langle \bar{\xi }\left(\stackrel{\to }{p},r\right)|\eta \left(\stackrel{\to }{p},r\right)\rangle \end{array}$ (42)

For the similar case of coherent states see [13] [14] .

Now

$\langle \bar{\zeta }\left(\stackrel{\to }{p},r\right)|\xi \left(\stackrel{\to }{p},r\right)\rangle =\exp \left[-\bar{\zeta }\left(\stackrel{\to }{p},r\right)\xi \left(\stackrel{\to }{p},r\right)\right]$ (43)

and

$\langle \bar{\xi }\left(\stackrel{\to }{p},r\right)|\eta \left(\stackrel{\to }{p},r\right)\rangle =\exp \left[-\bar{\xi }\left(\stackrel{\to }{p},r\right)\eta \left(\stackrel{\to }{p},r\right)\right]$ (44)

So, on evaluating the Grassmannian integral that appears we obtain

$\begin{array}{l}U\left(\bar{\zeta }\left(\stackrel{\to }{p},r\right),t_f;\eta \left(\stackrel{\to }{p},r\right),t_i;X,\bar{X}\right)\\ =\exp \{-\frac{\bar{\zeta }\left(\stackrel{\to }{p},r\right)\eta \left(\stackrel{\to }{p},r\right)}{1+{\text{e}}^{-i{E}_{\stackrel{\to }{p}}\left(t_f-t_i\right)}}+\ln \left(1+{\text{e}}^{-i{E}_{\stackrel{\to }{p}}\left(t_f-t_i\right)}\right)\underset{}{\begin{array}{c}\\ \end{array}}\\ +i\frac{m}{E_{\stackrel{\to }{p}}}{\displaystyle \underset{t_i}{\overset{t_f}{\int }}\text{d}t\left(\bar{\zeta }\left(\stackrel{\to }{p},r\right)\frac{{\text{e}}^{i{E}_{\stackrel{\to }{p}}t}}{{\text{e}}^{i{E}_{\stackrel{\to }{p}}{t}_i}+{\text{e}}^{i{E}_{\stackrel{\to }{p}}{t}_f}}\chi \left(\stackrel{\to }{p},r,t\right)+{\chi }^{\ast }\left(\stackrel{\to }{p},r,t\right)\frac{{\text{e}}^{-i{E}_{\stackrel{\to }{p}}t}}{{\text{e}}^{-i{E}_{\stackrel{\to }{p}}{t}_i}+{\text{e}}^{-i{E}_{\stackrel{\to }{p}}{t}_f}}\eta \left(\stackrel{\to }{p},r\right)\right)}\\ -{\left(\frac{m}{E_{\stackrel{\to }{p}}}\right)}^2{\displaystyle \underset{t_i}{\overset{t_f}{\int }}{\displaystyle \underset{t_i}{\overset{t}{\int }}\text{d}t}\text{d}{t}^{\prime }{\chi }^{\ast }\left(\stackrel{\to }{p},r,t\right)\lambda \left(\stackrel{\to }{p},t_f,t_i,t,t^{\prime }\right)\chi \left(\stackrel{\to }{p},r,t^{\prime }\right)}\}\end{array}$ (45)

We have set

$\lambda \left(\stackrel{\to }{p},t_f,t_i,t,t^{\prime }\right)={\text{e}}^{-i{E}_{\stackrel{\to }{p}}\left(t-t^{\prime }\right)}-\frac{2\cos \left(E_{\stackrel{\to }{p}}\left(t-t^{\prime }\right)\right)}{1+{\text{e}}^{i{E}_{\stackrel{\to }{p}}\left(t_f-t_i\right)}}=-i\frac{\sin \left(E_{\stackrel{\to }{p}}\left(t-t^{\prime }\right)-\frac{E_{\stackrel{\to }{p}}\left(t_f-t_i\right)}{2}\right)}{\cos \left(\frac{E_{\stackrel{\to }{p}}\left(t_f-t_i\right)}{2}\right)}$ (46)

Finally

$\begin{array}{l}U\left(\bar{\zeta }\left(\stackrel{\to }{p},r\right),t_f;\eta \left(\stackrel{\to }{p},r\right),t_i;X,\bar{X}\right)\\ =\exp \{-\frac{\bar{\zeta }\left(\stackrel{\to }{p},r\right)\eta \left(\stackrel{\to }{p},r\right)}{1+{\text{e}}^{-i{E}_{\stackrel{\to }{p}}\left(t_f-t_i\right)}}+\ln \left(1+{\text{e}}^{-i{E}_{\stackrel{\to }{p}}\left(t_f-t_i\right)}\right)\begin{array}{c}\\ \\ \\ \end{array}\\ +i\frac{m}{E_{\stackrel{\to }{p}}}{\displaystyle \underset{t_i}{\overset{t_f}{\int }}\text{d}t\left(\bar{\zeta }\left(\stackrel{\to }{p},r\right)\frac{{\text{e}}^{i{E}_{\stackrel{\to }{p}}t}}{{\text{e}}^{i{E}_{\stackrel{\to }{p}}{t}_i}+{\text{e}}^{i{E}_{\stackrel{\to }{p}}{t}_f}}\chi \left(\stackrel{\to }{p},r,t\right)+{\chi }^{\ast }\left(\stackrel{\to }{p},r,t\right)\frac{{\text{e}}^{-i{E}_{\stackrel{\to }{p}}t}}{{\text{e}}^{-i{E}_{\stackrel{\to }{p}}{t}_i}+{\text{e}}^{-i{E}_{\stackrel{\to }{p}}{t}_f}}\eta \left(\stackrel{\to }{p},r\right)\right)}\\ +i{\left(\frac{m}{E_{\stackrel{\to }{p}}}\right)}^2{\displaystyle \underset{t_i}{\overset{t_f}{\int }}{\displaystyle \underset{t_i}{\overset{t_f}{\int }}\text{d}t}\text{d}{t}^{\prime }{\chi }^{\ast }\left(\stackrel{\to }{p},r,t\right)\Theta \left(t-t^{\prime }\right)\frac{\sin \left(E_{\stackrel{\to }{p}}\left(t-t^{\prime }\right)-\frac{E_{\stackrel{\to }{p}}\left(t_f-t_i\right)}{2}\right)}{\cos \left(\frac{E_{\stackrel{\to }{p}}\left(t_f-t_i\right)}{2}\right)}\chi \left(\stackrel{\to }{p},r,t^{\prime }\right)}\}\end{array}$ (47)

$\Theta \left(t-t^{\prime }\right)$ is the step function.

We can obtain the finite time domain Green function of Dirac fields from the present considerations. We do that in the next section.

3. Green Function

According to the discussion of the previous section in the case of the Hamiltonian (23) the vacuum-to-vacuum amplitude in the presence of sources is

$\begin{array}{l}U\left(0,t_f;0,t_i;X,\bar{X}\right)=\exp \{\ln \left(1+{\text{e}}^{-i{E}_{\stackrel{\to }{p}}\left(t_f-t_i\right)}\right)\begin{array}{c}\\ \\ \\ \end{array}\\ +i{\left(\frac{m}{E_{\stackrel{\to }{p}}}\right)}^2{\displaystyle \underset{t_i}{\overset{t_f}{\int }}{\displaystyle \underset{t_i}{\overset{t_f}{\int }}\text{d}t}\text{d}{t}^{\prime }{\chi }^{\ast }\left(\stackrel{\to }{p},r,t\right)\Theta \left(t-t^{\prime }\right)\frac{\sin \left(E_{\stackrel{\to }{p}}\left(t-t^{\prime }\right)-\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{\cos \left(\frac{E_{\stackrel{\to }{p}}T}{2}\right)}\chi \left(\stackrel{\to }{p},r,t^{\prime }\right)\}}\end{array}$ (48)

where $T=t_f-t_i$ .

In the case of the Hamiltonian (22) we can proceed via similar steps to arrive to a superposition of expressions of the form (48). In our manipulations we have to take into account that ${\epsilon }_r,r=3,4$ is negative. Therefore the sign of time is modified (see Equation (50) below).

Moreover, we transform the functional dependence on $\chi ,{\chi }^{\ast }$ back to the dependence on $X,\bar{X}$ . To achieve that we make use of the orthonormality of the w spinors

${\epsilon }_r\bar{w}\left(\stackrel{\to }{p},r\right)w\left(\stackrel{\to }{p},r^{\prime }\right)={\delta }_{r{r}^{\prime }}$ (49)

Then we obtain the generating functional $Z\left(X,\bar{X}\right)$ of the correlation functions of the Dirac Lagrangian in the case of a finite time domain in the following form

$\begin{array}{l}Z\left(X,\bar{X}\right)=Z\left(0,0\right)\exp \{i{\displaystyle \underset{t_i}{\overset{t_f}{\int }}{\displaystyle \underset{t_i}{\overset{t_f}{\int }}\text{d}t}\text{d}{t}^{\prime }{\displaystyle \int \frac{{\text{d}}^{3}p}{{\left(2\pi \right)}^3}\frac{m}{E_{\stackrel{\to }{p}}}}{\left(\frac{m}{E_{\stackrel{\to }{p}}}\right)}^2}\begin{array}{c}\\ \\ \\ \end{array}\\ \times ({\displaystyle \underset{r,r^{\prime }=1}{\overset{2}{\sum }}{\chi }^{\ast }\left(\stackrel{\to }{p},r,t\right)\bar{w}\left(\stackrel{\to }{p},r\right)\Theta \left(t-t^{\prime }\right)}\frac{\sin \left(E_{\stackrel{\to }{p}}\left(t-t^{\prime }\right)-\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{\cos \left(\frac{E_{\stackrel{\to }{p}}T}{2}\right)}w\left(\stackrel{\to }{p},r^{\prime }\right)\chi \left(\stackrel{\to }{p},r^{\prime },t^{\prime }\right)\\ -{\displaystyle \underset{r,r^{\prime }=3}{\overset{4}{\sum }}{\chi }^{\ast }\left(\stackrel{\to }{p},r,t\right)\bar{w}\left(\stackrel{\to }{p},r\right)\Theta \left(t^{\prime }-t\right)}\frac{\sin \left(E_{\stackrel{\to }{p}}\left(t^{\prime }-t\right)-\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{\cos \left(\frac{E_{\stackrel{\to }{p}}T}{2}\right)}w\left(\stackrel{\to }{p},r^{\prime }\right)\chi \left(\stackrel{\to }{p},r^{\prime },t^{\prime }\right))\}\end{array}$ (50)

Now since

$\left(\cancel{p}-{\epsilon }_{r}m\right)w\left(\stackrel{\to }{p},r\right)=0$ (51)

we can write

${\displaystyle \underset{r^{\prime }=1}{\overset{2}{\sum }}{\displaystyle \underset{r=1}{\overset{2}{\sum }}\bar{w}\left(\stackrel{\to }{p},r\right)w\left(\stackrel{\to }{p},r^{\prime }\right)}}={\displaystyle \underset{r,r^{\prime }=1}{\overset{4}{\sum }}\bar{w}\left(\stackrel{\to }{p},r\right)\left(\frac{\cancel{p}+m}{2m}\right)w\left(\stackrel{\to }{p},r^{\prime }\right)}$ (52)

and

${\displaystyle \underset{r^{\prime }=3}{\overset{4}{\sum }}{\displaystyle \underset{r=3}{\overset{4}{\sum }}\bar{w}\left(\stackrel{\to }{p},r\right)w\left(\stackrel{\to }{p},r^{\prime }\right)}}={\displaystyle \underset{r,r^{\prime }=1}{\overset{4}{\sum }}\bar{w}\left(\stackrel{\to }{p},r\right)\left(\frac{\cancel{p}-m}{2m}\right)w\left(\stackrel{\to }{p},r^{\prime }\right)}$ (53)

So on using the above equations, Equation (50) becomes

$\begin{array}{l}Z\left(X,\bar{X}\right)=Z\left(0,0\right)\\ \times \exp \{i{\displaystyle \underset{t_i}{\overset{t_f}{\int }}{\displaystyle \underset{t_i}{\overset{t_f}{\int }}\text{d}t}\text{d}{t}^{\prime }{\displaystyle \int {\text{d}}^{3}x}{\displaystyle \int {\text{d}}^3{x}^{\prime }}{\displaystyle \int \frac{{\text{d}}^{3}p}{{\left(2\pi \right)}^3}}{\displaystyle \underset{r=1}{\overset{4}{\sum }}{\displaystyle \int \frac{{\text{d}}^3{p}^{\prime }}{{\left(2\pi \right)}^3}}}\frac{m}{E_{{\stackrel{\to }{p}}^{\prime }}}{\chi }^{\ast }\left({\stackrel{\to }{p}}^{\prime },r,t\right)\bar{w}\left({\stackrel{\to }{p}}^{\prime },r\right){\text{e}}^{-i{\stackrel{\to }{p}}^{\prime }\cdot \stackrel{\to }{x}}}\frac{\Theta \left(t-t^{\prime }\right)}{2E_{\stackrel{\to }{p}}}\\ \times \left(\cancel{p}+m\right)\frac{\sin \left(E_{\stackrel{\to }{p}}(t-t^{\prime })-\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{\cos \left(\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{\text{e}}^{i\stackrel{\to }{p}\cdot \left(\stackrel{\to }{x}-{\stackrel{\to }{x}}^{\prime }\right)}{\displaystyle \underset{r^{\prime }=1}{\overset{4}{\sum }}{\displaystyle \int \frac{{\text{d}}^3{p}^{″}}{{\left(2\pi \right)}^3}}}\frac{m}{E_{{\stackrel{\to }{p}}^{″}}}w\left({\stackrel{\to }{p}}^{″},r^{\prime }\right)\chi \left({\stackrel{\to }{p}}^{″},r^{\prime },t^{\prime }\right){\text{e}}^{i{\stackrel{\to }{p}}^{″}\cdot {\stackrel{\to }{x}}^{\prime }}\\ -{\displaystyle \underset{r=1}{\overset{4}{\sum }}{\displaystyle \int \frac{{\text{d}}^3{p}^{\prime }}{{\left(2\pi \right)}^3}}}\frac{m}{E_{{\stackrel{\to }{p}}^{\prime }}}{\chi }^{\ast }\left(-{\stackrel{\to }{p}}^{\prime },r,t\right)\bar{w}\left(-{\stackrel{\to }{p}}^{\prime },r\right){\text{e}}^{-i{\stackrel{\to }{p}}^{\prime }\cdot \stackrel{\to }{x}}\frac{\Theta \left(t^{\prime }-t\right)}{2E_{\stackrel{\to }{p}}}\left(\cancel{p}-m\right)\frac{\sin \left(E_{\stackrel{\to }{p}}\left(t^{\prime }-t\right)-\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{\cos \left(\frac{E_{\stackrel{\to }{p}}T}{2}\right)}\\ \times {\text{e}}^{-i\stackrel{\to }{p}\cdot \left(\stackrel{\to }{x}-{\stackrel{\to }{x}}^{\prime }\right)}{\displaystyle \underset{r^{\prime }=1}{\overset{4}{\sum }}{\displaystyle \int \frac{{\text{d}}^3{p}^{″}}{{\left(2\pi \right)}^3}}}\frac{m}{E_{{\stackrel{\to }{p}}^{″}}}w\left(-{\stackrel{\to }{p}}^{″},r^{\prime }\right)\chi \left(-{\stackrel{\to }{p}}^{″},r^{\prime },t^{\prime }\right){\text{e}}^{i{\stackrel{\to }{p}}^{″}\cdot {\stackrel{\to }{x}}^{\prime }}\}\end{array}$ (54)

Therefore, since the Green function is given as

$\begin{array}{c}G\left(\stackrel{\to }{x}-{\stackrel{\to }{x}}^{\prime },t-t^{\prime };T\right)=\langle 0|T\left\{\Psi \left(t,\stackrel{\to }{x}\right)\bar{\Psi }\left(t^{\prime },{\stackrel{\to }{x}}^{\prime }\right)\right\}|0\rangle \\ =-\frac{1}{Z\left(0,0\right)}{\frac{{\delta }^2}{\delta \bar{X}\delta X}Z\left(X,\bar{X}\right)|}_{X=\bar{X}=0}\end{array}$ (55)

upon performing the functional derivations, we get

$\begin{array}{l}G\left(\stackrel{\to }{x}-{\stackrel{\to }{x}}^{\prime },t-t^{\prime };T\right)\\ =-i{\displaystyle \int \frac{{\text{d}}^{3}p}{{\left(2\pi \right)}^3}}(\frac{\Theta \left(t-t^{\prime }\right)}{2E_{\stackrel{\to }{p}}}\left(\cancel{p}+m\right)\frac{\sin \left(E_{\stackrel{\to }{p}}\left(t-t^{\prime }\right)-\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{\cos \left(\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{\text{e}}^{i\stackrel{\to }{p}\cdot \left(\stackrel{\to }{x}-{\stackrel{\to }{x}}^{\prime }\right)}\\ +\frac{\Theta \left(t^{\prime }-t\right)}{2E_{\stackrel{\to }{p}}}\left(\cancel{p}-m\right)\frac{\sin \left(E_{\stackrel{\to }{p}}\left(t-t^{\prime }\right)+\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{\cos \left(\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{\text{e}}^{-i\stackrel{\to }{p}\cdot \left(\stackrel{\to }{x}-{\stackrel{\to }{x}}^{\prime }\right)})\end{array}$ (56)

or

$\begin{array}{l}G\left(\stackrel{\to }{x}-{\stackrel{\to }{x}}^{\prime },t-t^{\prime };T\right)\\ =-i{\displaystyle \int \frac{{\text{d}}^{3}p}{{\left(2\pi \right)}^3}}(\frac{\Theta \left(t-t^{\prime }\right)}{E_{\stackrel{\to }{p}}}\left(\cancel{p}+m\right)\frac{\sin \left(E_{\stackrel{\to }{p}}\left(t-t^{\prime }\right)-\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{1+{\text{e}}^{-i{E}_{\stackrel{\to }{p}}T}}{\text{e}}^{-i\frac{E_{\stackrel{\to }{p}}T}{2}}{\text{e}}^{i\stackrel{\to }{p}\cdot \left(\stackrel{\to }{x}-{\stackrel{\to }{x}}^{\prime }\right)}\\ +\frac{\Theta \left(t^{\prime }-t\right)}{E_{\stackrel{\to }{p}}}\left(\cancel{p}-m\right)\frac{\sin \left(E_{\stackrel{\to }{p}}\left(t-t^{\prime }\right)+\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{1+{\text{e}}^{-i{E}_{\stackrel{\to }{p}}T}}{\text{e}}^{-i\frac{E_{\stackrel{\to }{p}}T}{2}}{\text{e}}^{-i\stackrel{\to }{p}\cdot \left(\stackrel{\to }{x}-{\stackrel{\to }{x}}^{\prime }\right)})\end{array}$ (57)

Further after appropriate geometric series expansions Equations (56, 57) can be written in the form

$\begin{array}{l}G\left(\stackrel{\to }{x},\tau ;T\right)\\ ={\displaystyle \int \frac{{\text{d}}^{3}p}{{\left(2\pi \right)}^3}}[\frac{\Theta \left(\tau \right)}{2E_{\stackrel{\to }{p}}}\left(\cancel{p}+m\right){\text{e}}^{i\stackrel{\to }{p}\cdot \stackrel{\to }{x}}\left({\text{e}}^{-i{E}_{\stackrel{\to }{p}}\tau }{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{\left(-1\right)}^n{\text{e}}^{-in{E}_{\stackrel{\to }{p}}T}}-{\text{e}}^{i{E}_{\stackrel{\to }{p}}\tau }{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{\left(-1\right)}^n{\text{e}}^{-i\left(n+1\right)E_{\stackrel{\to }{p}}T}}\right)\\ -\frac{\Theta \left(-\tau \right)}{2E_{\stackrel{\to }{p}}}\left(\cancel{p}-m\right){\text{e}}^{-i\stackrel{\to }{p}\cdot \stackrel{\to }{x}}\left({\text{e}}^{i{E}_{\stackrel{\to }{p}}\tau }{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{\left(-1\right)}^n{\text{e}}^{-in{E}_{\stackrel{\to }{p}}T}}-{\text{e}}^{-i{E}_{\stackrel{\to }{p}}\tau }{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{\left(-1\right)}^n{\text{e}}^{-i\left(n+1\right)E_{\stackrel{\to }{p}}T}}\right)]\end{array}$ (58)

We should expect that after the integrations the above series converge and therefore, we can truncate them. Alternatively, we can bypass the poles in Equation (57) if we introduce a constant $\mu$ which is smaller but close to one and write Equation (57) in the form

$\begin{array}{l}G\left(\stackrel{\to }{x}-{\stackrel{\to }{x}}^{\prime },t-t^{\prime };T\right)\\ =-i{\displaystyle \int \frac{{\text{d}}^{3}p}{{\left(2\pi \right)}^3}}(\frac{\Theta \left(t-t^{\prime }\right)}{E_{\stackrel{\to }{p}}}\left(\cancel{p}+m\right)\frac{\sin \left(E_{\stackrel{\to }{p}}\left(t-t^{\prime }\right)-\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{1+\mu {\text{e}}^{-i{E}_{\stackrel{\to }{p}}T}}{\text{e}}^{-i\frac{E_{\stackrel{\to }{p}}T}{2}}{\text{e}}^{i\stackrel{\to }{p}\cdot \left(\stackrel{\to }{x}-{\stackrel{\to }{x}}^{\prime }\right)}\end{array}$ (59)

$+\frac{\Theta \left(t^{\prime }-t\right)}{E_{\stackrel{\to }{p}}}\left(\cancel{p}-m\right)\frac{\sin \left(E_{\stackrel{\to }{p}}\left(t-t^{\prime }\right)+\frac{E_{\stackrel{\to }{p}}T}{2}\right)}{1+\mu {\text{e}}^{-i{E}_{\stackrel{\to }{p}}T}}{\text{e}}^{-i\frac{E_{\stackrel{\to }{p}}T}{2}}{\text{e}}^{-i\stackrel{\to }{p}\cdot \left(\stackrel{\to }{x}-{\stackrel{\to }{x}}^{\prime }\right)})$

We can use the above expressions in the study of the propagation of Dirac fields in a finite time domain spacetime.

4. Application

Now we apply the above theory to the propagation of a Dirac particle interacting with an external (classical) electromagnetic field characterized by its potential $A_{\mu }$ . Then the action will have the form

$I\left(\Psi ,A\right)={\displaystyle \int \text{d}\tau }{\displaystyle \int {\text{d}}^{3}x\left[\bar{\Psi }\left(i{\gamma }^{\mu }{\partial }_{\mu }-e{\gamma }^{\mu }{A}_{\mu }-m\right)\Psi \right]}$ (60)

and according to variational considerations $\Psi$ satisfies the equation

$\left(i{\gamma }^{\mu }{\partial }_{\mu }-e{\gamma }^{\mu }{A}_{\mu }-m\right)\Psi =0$ (61)

while the corresponding Green function $G_A\left({\stackrel{\to }{x}}_2,{\tau }_2;{\stackrel{\to }{x}}_1,{\tau }_1;T\right)$ obeys the equation

$\left[i{\cancel{\partial }}_2-e\cancel{A}\left({\stackrel{\to }{x}}_2,{\tau }_2\right)-m\right]G_A\left({\stackrel{\to }{x}}_2,{\tau }_2;{\stackrel{\to }{x}}_1,{\tau }_1;T\right)=i{\delta }^{\left(3\right)}\left({\stackrel{\to }{x}}_2-{\stackrel{\to }{x}}_1\right)\delta \left({\tau }_2-{\tau }_1\right)$ (62)

Green functions are important as functionally they are the inverses of the dynamic operators describing the evolution of the various systems. So combined with perturbation theory they constitute a powerful tool. Below we apply that mathematical structure to the present system.

In fact here we intend to consider the time evolution of a Dirac spinor and calculate its probability density as a function of time. Let initially the Dirac particle spinor be $\psi \left(\stackrel{\to }{y},0\right)=\phi \left(\stackrel{\to }{y}\right)$ . Then the final spinor $\psi \left(\stackrel{\to }{x},T\right)$ is

$\psi \left(\stackrel{\to }{x},T\right)={\displaystyle \int {\text{d}}^{3}y{G}_A\left(\stackrel{\to }{x},T;\stackrel{\to }{y},0;T\right){\gamma }^0\phi \left(\stackrel{\to }{y}\right)}$ (63)

and its four current $j^{\mu }\left(\stackrel{\to }{x},T\right)$ has the form

$j^{\mu }\left(\stackrel{\to }{x},T\right)=e\bar{\psi }\left(\stackrel{\to }{x},T\right){\gamma }^{\mu }\psi \left(\stackrel{\to }{x},T\right)$ (64)

Now we suppose that $e{\cancel{A}}_{\mu }$ is small enough to be treated as a perturbation so that $G_A$ may be expressed as an (asymptotic) expansion in $e{\cancel{A}}_{\mu }$ . Then via standard methods [2] we can get the integral equation

$\begin{array}{l}{G}_A\left({\stackrel{\to }{x}}_3,{\tau }_3;{\stackrel{\to }{x}}_1,{\tau }_1;T\right)\\ =G\left({\stackrel{\to }{x}}_3,{\tau }_3;{\stackrel{\to }{x}}_1,{\tau }_1;T\right)-i{\displaystyle \int {\text{d}}^3{\stackrel{\to }{x}}_2}{\displaystyle \underset{0}{\overset{T}{\int }}\text{d}{\tau }_2}G\left({\stackrel{\to }{x}}_3,{\tau }_3;{\stackrel{\to }{x}}_2,{\tau }_2;T\right)e\cancel{A}\left({\stackrel{\to }{x}}_2,{\tau }_2\right)G_A\left({\stackrel{\to }{x}}_2,{\tau }_2;{\stackrel{\to }{x}}_1,{\tau }_1;T\right)\end{array}$ (65)

where we have set (see Equation (56))

$G\left({\stackrel{\to }{x}}_3,{\tau }_3;{\stackrel{\to }{x}}_1,{\tau }_1;T\right)=G\left({\stackrel{\to }{x}}_3-{\stackrel{\to }{x}}_1,{\tau }_3-{\tau }_1;T\right)$ (66)

So, we suppose that $A_{\mu }$ is the potential of a plane electromagnetic wave propagating along the wavevector $\stackrel{\to }{k}$ , with frequency $\omega$ , polarization vector $\stackrel{\to }{\epsilon }$ and amplitude ${\Delta }_0$ Then

$\stackrel{\to }{A}\left(\stackrel{\to }{x},\tau \right)={\Delta }_0\left(\stackrel{\to }{\epsilon }{\text{e}}^{i\left(\omega \tau -\stackrel{\to }{k}\cdot \stackrel{\to }{x}\right)}+\stackrel{\to }{\epsilon }{\text{e}}^{-i\left(\omega \tau -\stackrel{\to }{k}\cdot \stackrel{\to }{x}\right)}\right)$ (67)

and

$A_0\left(\stackrel{\to }{x},\tau \right)=0$ (68)

Further we set

$\phi \left(\stackrel{\to }{y}\right)={\left(\frac{1}{\pi {\sigma }^2}\right)}^{3/4}{\text{e}}^{-\frac{{\stackrel{\to }{y}}^2}{2{\sigma }^2}}\left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right)$ (69)

On combining Equations (63, 65) we obtain to first order with respect to $\stackrel{\to }{A}$ the expression

$\begin{array}{c}\psi \left(\stackrel{\to }{x},T\right)={\displaystyle \int {\text{d}}^3\stackrel{\to }{y}G\left(\stackrel{\to }{x},T;\stackrel{\to }{y},0;T\right){\gamma }^0\phi \left(\stackrel{\to }{y}\right)}\\ -i{\displaystyle \underset{0}{\overset{T}{\int }}\text{d}{\tau }_2}{\displaystyle \iint {\text{d}}^3{\stackrel{\to }{x}}_2}{\text{d}}^3\stackrel{\to }{y}G\left(\stackrel{\to }{x},T;{\stackrel{\to }{x}}_2,{\tau }_2;T\right)e\cancel{A}\left({\stackrel{\to }{x}}_2,{\tau }_2\right)G\left({\stackrel{\to }{x}}_2,{\tau }_2;\stackrel{\to }{y},0;T\right){\gamma }^0\phi \left(\stackrel{\to }{y}\right)\end{array}$ (70)

Then upon using Equation (56) and substituting Equations (67, 68, 69) we get

$\begin{array}{c}{\psi }_{\delta }\left(\stackrel{\to }{x},T\right)=-i{\displaystyle \int \frac{{\text{d}}^{3}p}{{\left(2\pi \right)}^3}}\frac{1}{2E_{\stackrel{\to }{p}}}{\left(\cancel{p}+m\right)}_{\delta 1}{\text{e}}^{i\stackrel{\to }{p}\cdot \stackrel{\to }{x}}{\left(4\pi {\sigma }^2\right)}^{3/4}{\text{e}}^{-\frac{{\sigma }^2{\stackrel{\to }{p}}^2}{2}}\tan \left(\frac{E_{\stackrel{\to }{p}}T}{2}\right)\\ -ie{\Delta }_0{\displaystyle \underset{\alpha ,\beta }{\sum }{\displaystyle \underset{0}{\overset{T}{\int }}\text{d}{\tau }_2}}{\displaystyle \iint \frac{{\text{d}}^3{p}_1{\text{d}}^3{p}_2}{{\left(2\pi \right)}^3}}\frac{1}{2E_{{\stackrel{\to }{p}}_1}}{\left({\cancel{p}}_1+m\right)}_{\delta \beta }{\text{e}}^{i{\stackrel{\to }{p}}_1\cdot \stackrel{\to }{x}}\frac{\sin \left(E_{{\stackrel{\to }{p}}_1}{\tau }_2-\frac{E_{{\stackrel{\to }{p}}_1}T}{2}\right)}{\cos \left(\frac{E_{{\stackrel{\to }{p}}_1}T}{2}\right)}\\ \times \left({\text{e}}^{i\omega {\tau }_2}{\delta }^{\left(3\right)}\left({\stackrel{\to }{p}}_1+\stackrel{\to }{k}-{\stackrel{\to }{p}}_2\right)+{\text{e}}^{-i\omega {\tau }_2}{\delta }^{\left(3\right)}\left({\stackrel{\to }{p}}_1-\stackrel{\to }{k}-{\stackrel{\to }{p}}_2\right)\right)\\ \times {\cancel{\epsilon }}_{\beta \alpha }\frac{1}{2E_{{\stackrel{\to }{p}}_2}}{\left({\cancel{p}}_2+m\right)}_{\alpha 1}{\left(4\pi {\sigma }^2\right)}^{3/4}{\text{e}}^{-\frac{{\sigma }^2{\stackrel{\to }{p}}_2^2}{2}}\frac{\sin \left(E_{{\stackrel{\to }{p}}_2}{\tau }_2-\frac{E_{{\stackrel{\to }{p}}_2}T}{2}\right)}{\cos \left(\frac{E_{{\stackrel{\to }{p}}_2}T}{2}\right)}\end{array}$ (71)

We notice that $e{\Delta }_0$ has dimension of energy (see the comments at the end of the introduction as well).

After appropriate manipulations (see Equation (59) and the comments above that equation) we can derive the following form for the $\psi$ spinor

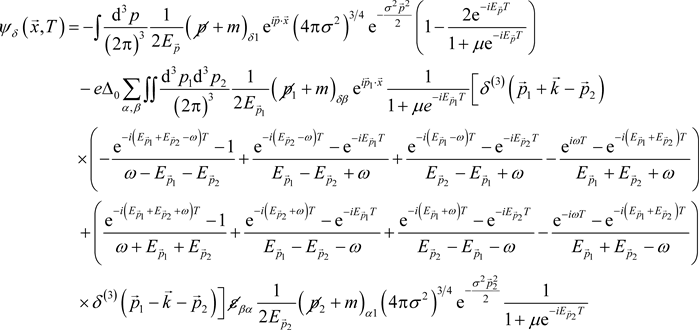(72)

Moreover according to Equation (64) the probability density has the form

$\rho \left(\stackrel{\to }{x},T\right)=\bar{\psi }\left(\stackrel{\to }{x},T\right){\gamma }^0\psi \left(\stackrel{\to }{x},T\right)={\psi }^{+}\left(\stackrel{\to }{x},T\right)\psi \left(\stackrel{\to }{x},T\right)={\displaystyle \underset{\delta =1}{\overset{4}{\sum }}{\left|{\psi }_{\delta }\left(\stackrel{\to }{x},T\right)\right|}^2}$ (73)

If $T=0$ as we can easily conclude from Equation (69) the probability density is spherically symmetric. Moreover, if we let the polarization vector $\epsilon$ be along the x-axis and the wavevector along the z-axis. I.e.

$\epsilon =\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right)$ (74)

and

$\stackrel{\to }{k}=\left(0,0,k\right)$ (75)

We can use the above considerations to extract the probability density $\rho$ for various times T. In Figure 1 we give several contour plots. We observe that the probability density spreads and that the particle moves away from its initial position.

Figure 1. Contour plots of the probability density of a Dirac particle interacting with a plane electromagnetic wave which is linearly polarized along the x-axis and propagates along the z-axis. We consider contour plots on various planes and for various times T. For $T=0$ the probability density is spherically symmetric. So, we give one of the identical contour plot and on setting $\stackrel{\to }{x}=\left(x_1,x_2,x_3\right)=\left(x,y,z\right)$ we suppose that (i, j, k) is a permutation of (1, 2, 3). For larger times we observe that the particle spreads and moves in space. Moreover we have used the values $\omega =0.3$ , $k=0.3$ , ${\Delta }_0=5.0$ , $\sigma =1.0$ , $\mu =0.9$ and have applied natural units. I.e. we have set $m=c=\hslash =1$ .

5. Conclusions

In the present paper, we considered the case of a Dirac field in a finite time do-main. We expanded its Hamiltonian in terms of creation and annihilation operators and path integrated via Grassmann variables techniques to extract its Green function. We notice that the finite time domain Green function appears when the boundary conditions correspond to a finite time interval.

Moreover, we applied that Green function in the perturbative study of its interaction with a classical electromagnetic field and considered the time evolution of an initially Gaussian spinor. We kept first order terms with respect the field and as an application we gave contours plots of the probability density on various planes and for various times. From those contour plots we can observe that the probability density of the particle as a function of time spreads and that the particle moves away from its initial position due to the interaction.

In conclusion the present method—structure can be applied to various quantum systems and give interesting results concerning their finite time domain dynamics. In subsequent publications we intend to consider the case of other quantum fields, free or interacting, within finite time domains and study their dynamics.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Zinn-Justin, J. (1996) Quantum Field Theory and Critical Phenomena. 3rd Edition, Oxford University Press, New York.
[2]	Itzykson, C. and Zuber, J.-B. (1980) Quantum Field Theory. McGraw Hill, Singapore.
[3]	Hatfield, B. (1992) Quantum Field Theory of Point Particles and Strings. Westview Press, Boulder.
[4]	Kaku, M. (1993) Quantum Field Theory, A Modern Introduction. Oxford University Press, New York.
[5]	Nomoto, K. and Fukuda, R. (1991) Quantum Field Theory with Finite Time Interval-Application to QED. Progress in Theoretical Physics, 86, 269-302. https://doi.org/10.1143/ptp/86.1.269
[6]	Arda, A. and Sever, R. (2016) Exact Solutions of Effective-Mass Dirac-Pauli Equation with an Electromagnetic Field. Few-Body Systems, 58, Article No. 7.
[7]	Vladislav, V., Kravchenko, M.P. and Rammirez, T. (2000) New Exact Solutions of the Massive Dirac Equation with Electric or Scalar Potential. Mathematical Methods in the Applied Sciences, 23, 769-776.
[8]	Gulveren, B., Demirtas, A. and Ogul, R. (2001) Solution of the Dirac Equation for a Dirac Particle in a Yukawa Field. Physica Scripta, 64, 277-278. https://doi.org/10.1238/Physica.Regular.064a00277
[9]	Cazenave, T. and Vazquez, L. (1986) Existence of Localized Solutions for a Classical Nonlinear Dirac Field. Communications in Mathematical Physics, 105, 35-47. https://doi.org/10.1007/BF01212340
[10]	Lam, Y.-M.P. (1972) Perturbation Lagrangian Theory for Dirac Fields-Ward-Takahashi Identity and Current Algebra. Physical Review D, 6, 2161-2167. https://doi.org/10.1103/PhysRevD.6.2161
[11]	Cotaescu, I.I. (2020) Time Evolution of the Free Dirac Field in Spatially Flat FLRW Spacetimes. International Journal of Modern Physics A, 35, Article No. 2030019. https://doi.org/10.1142/S0217751X20300197
[12]	Ohnuki, Y. and Kashiwa T. (1978) Coherent States of Fermi Operators and the Path Integral. Progress of Theoretical Physics, 60, 548-564. https://doi.org/10.1143/PTP.60.548
[13]	Thrapsaniotis, E.G. (2001) Propagator of an Electron in a Cavity in the Presence of a Coherent Photonic Field. European Physical Journal D, 14, 43-47. https://doi.org/10.1007/s100530170233
[14]	Thrapsaniotis, E.G. (2017) Atoms-Photonic Field Interaction: Influence Functional and Perturbation Theory. In: Uzunov, D.I., Ed., Recent Studies in Perturbation Theory, InTechOpen, London. https://doi.org/10.5772/67774