Stochastic Chaos of Exponential Oscillons and Pulsons

Victor A. Miroshnikov

Department of Mathematics and Data Analytics, College of Mount Saint Vincent, New York, USA.

DOI: 10.4236/ajcm.2023.134030                

Abstract

An exact three-dimensional solution for stochastic chaos of I wave groups of M random internal waves governed by the Navier-Stokes equations is developed. The Helmholtz decomposition is used to expand the Dirichlet problem for the Navier-Stokes equations into the Archimedean, Stokes, and Navier problems. The exact solution is obtained with the help of the method of decomposition in invariant structures. Differential algebra is constructed for six families of random invariant structures: random scalar kinematic structures, time-complementary random scalar kinematic structures, random vector kinematic structures, time-complementary random vector kinematic structures, random scalar dynamic structures, and random vector dynamic structures. Tedious computations are performed using the experimental and theoretical programming in Maple. The random scalar and vector kinematic structures and the time-complementary random scalar and vector kinematic structures are applied to solve the Stokes problem. The random scalar and vector dynamic structures are employed to expand scalar and vector variables of the Navier problem. Potentialization of the Navier field becomes available since vortex forces, which are expressed via the vector potentials of the Helmholtz decomposition, counterbalance each other. On the contrary, potential forces, which are described by the scalar potentials of the Helmholtz decomposition, superimpose to generate the gradient of a dynamic random pressure. Various constituents of the kinetic energy are ascribed to diverse interactions of random, three-dimensional, nonlinear, internal waves with a two-fold topology, which are termed random exponential oscillons and pulsons. Quantization of the kinetic energy of stochastic chaos is developed in terms of wave structures of random elementary oscillons, random elementary pulsons, random internal, diagonal, and external elementary oscillons, random wave pulsons, random internal, diagonal, and external wave oscillons, random group pulsons, random internal, diagonal, and external group oscillons, a random energy pulson, random internal, diagonal, and external energy oscillons, and a random cumulative energy pulson.

Keywords

The Navier-Stokes Equations, Stochastic Chaos, Helmholtz Decomposition, Exact Solution, Decomposition into Invariant Structures, Experimental and Theoretical Programming, Quantization of Kinetic Energy, Random Elementary Oscillon, Random Elementary Pulson, Random Internal Elementary Oscillon, Random Diagonal Elementary Oscillon, Random External Elementary Oscillon, Random Wave Pulson, Random Internal Wave Oscillon, Random Diagonal Wave Oscillon, Random External Wave Oscillon, Random Group Pulson, Random Internal Group Oscillon, Random Diagonal Group Oscillon, Random External Group Oscillon, Random Energy Pulson, Random Internal Energy Oscillon, Random Diagonal Energy Oscillon, Random External Energy Oscillon, Random Cumulative Energy Pulson

1. Introduction

Deterministic chaos of exponential oscillons and pulsons was developed in [1] with the help of the method of Decomposition in Invariant Structures (DIS) [1] [2] [3] [4] , where a family of deterministic scalar and vector invariant structures have been constructed to solve the kinematic Stokes problem and the dynamic Navier problem. Quantization of the kinetic energy of the deterministic chaos has been treated for the Fourier set of wave parameters [3] and for the Bernoulli set of wave parameters [4] that enables to model turbulization of deterministic chaos.

The sequence of studies [1] [2] [3] [4] was initiated by paper [5] about conservative interaction of N three-dimensional internal waves controlled by the Navier-Stokes equations. The family of stationary kinematic Euler-Fourier functions of the later paper resulted in an extreme sophistication of the functional solution, which was derived with the help of experimental and theoretical programming in Maple, and inspired construction of the invariant structures in [1] [2] [3] [4] in order to make exact solutions of the Navier-Stokes equations more robust.

Another continuation of paper [5] was considered in the area of stochastic waves [6] , which model perturbations of deterministic waves. In [6] , smooth random functions of time are used as wave parameters of stochastic waves. However, the obtained results are limited by two dimensions and the nonstationary kinematic Euler-Fourier functions. The purpose of the current paper is development of the structural approach to stochastic, three-dimensional, nonlinear, internal waves governed by the Navier-Stokes equations.

The contents of this paper are as follows. Theoretical Random Scalar Kinematic (tRSK) structures, experimental Random Scalar Kinematic (eRSK) structures, time-complementary tRSK (tRSK_t) structures, and time-complementary eRSK (eRSK_t) structures are systematically developed in Section 2. In Section 3, the random scalar kinematic structures are complemented by experimental Random Vector Kinematic (eRVK) structures, theoretical Random Vector Kinematic (tRVK) structures, time-complementary eRVK (eRVK_t) structures, and time-complementary tRVK (tRVK_t) structures. The random scalar and vector kinematic structures and the time-complementary random scalar and vector kinematic structures are utilized to find scalar and vector variables of the kinematic Stokes problem. Section 4 deals with experimental Random-Random Scalar Dynamic (eRRSD) structures and theoretical Random-Random Scalar Dynamic (tRRSD) structures, which are required to describe scalar variables of the dynamic Navier problem. To express vector variables of this problem, experimental Random-Random Vector Dynamic (eRRVD) structures and theoretical Random-Random Vector Dynamic (tRRVD) structures of the mth and nth families are introduced and studied in Section 5. The Helmholtz decomposition of the random Navier-Stokes problem into the Archimedean, the random Stokes, and the random Navier problems is considered in Section 6, where a kinematic solution of the random Stokes problem, which is subjected to the Dirichlet boundary conditions and conditions at infinities, is obtained. A dynamic solution of the random Navier problem is computed and verified in Section 7 with the help of the tRRSD and tRRVD structures. Section 8 is devoted to decomposition of a matrix of the kinetic energy of the stochastic chaos of exponential oscillons and pulsons. Random wave pulsons, random group pulsons, and a random energy pulson are described in Section 9, which is proceeded by Section 10 dealing with random diagonal wave oscillons, random diagonal group oscillons, and a random diagonal energy oscillon. In Section 11, we treat random internal wave oscillons, random internal group oscillons, and a random internal energy oscillon. Section 12 is dedicated to random external wave oscillons, random external group oscillons, and a random external energy oscillon. Random elementary pulsons, random internal elementary oscillons, random diagonal elementary oscillons, and random external elementary oscillons are represented in Section 13. Session 14 contains a summary of quantization of the stochastic chaos of exponential oscillons and pulsons and a concise review of open problems.

2. Random Scalar Kinematic Structures

2.1. Definitions of the tRSK and eRSK Structures

Similar to the theoretical Deterministic Scalar Kinematic (tDSK) structures (13) of [1] , the tRSK structures s_r,i,m, s_r,x,i,m, s_r,y,i,m, s_r,x,y,i,m are defined as follows:

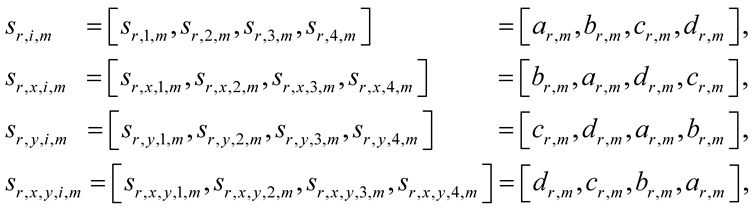(1)

where a_r,m, b_r,m, c_r,m, d_r,m are the eRSK structures, i = 1, 2, ¼, I = 1, 2, 3, 4 is a counter of random wave groups, and m = 1, 2, ¼, M is a counter of random internal waves.

The tRSK structures are [1, 4, M, 1] arrays, which are visualized by 1 ´ 4 rows of the eRSK structures (1) and by M ´ 4 matrices, for instance,

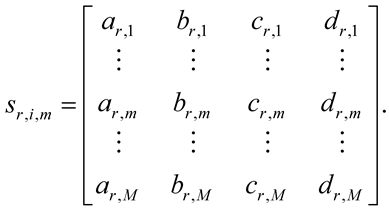(2)

Analogous to the experimental Deterministic Scalar Kinematic (eDSK) structures (1) of [1] , the eRSK structures are specified via the following relations:

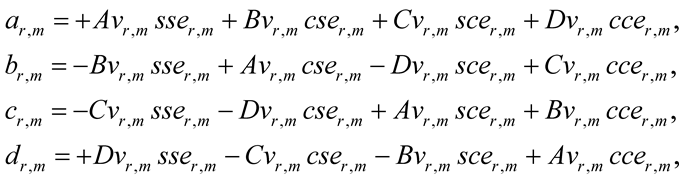(3)

where functional amplitudes of a harmonic variable v(x, y, z, t)

(4)

are smooth random functions of time from C^∞. If Av_r,m = 1, Bv_r,m = Cv_r,m = Dv_r,m = 0, the eRSK structures are reduced to the eRSK functions, i.e.

(5)

The eRSK structures are [M, 1] arrays, which are displayed via M ´ 1 columns, for example,

(6)

The three-variables (3-v) eRSK functions [sse_r,m, cse_r,m, sce_r,m, cce_r,m](X_r,m, Y_r,m, z) are products

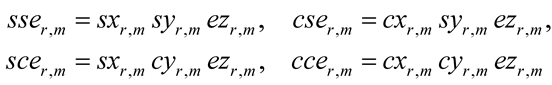(7)

of the following 1-v (one-variable) eRSK trigonometric functions [sx_r,m, cx_r,m](X_r,m), [sy_r,m, cy_r,m](Y_r,m) and an exponential function ez_r,m = ez_r,m(z)

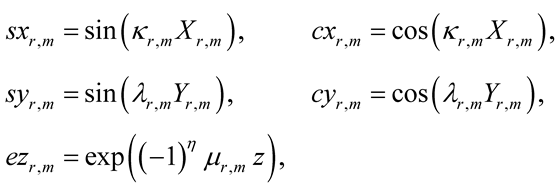(8)

where X_r,m = X_r,m(x, t) and Y_r,m = Y_r,m(y, t) are propagation variables defined by

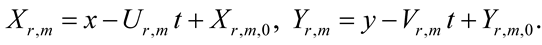(9)

In Equations (1)-(9), (x, y, z) is the Cartesian coordinate of a motionless frame of reference, t is time, (X_r,m, Y_r,m, z) is the Cartesian coordinate of a frame of reference moving with the mth random elementary oscillon (209)-(210), [U_r,m, V_r,m, 0] is a celerity of propagation, and [X_r,m,0, Y_r,m,0] is a reference value of [X_r,m, Y_r,m] at t = 0, x = 0, y = 0. A sign parameter η = 0 for z < 0 and η = 1 for z > 0, κ_r,m, λ_r,m, μ_r,m are wave numbers in the x-, y-, z-directions such that

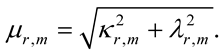(10)

The wave numbers are constants since otherwise the temporal derivative of the velocity potential does not commutate with the gradient. Propagation parameters

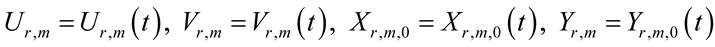(11)

together with (4) are smooth random functions of time from C^∞.

2.2. Definitions of the tRSK_t and eRSK_t Structures

We also define the tRSK_t structures

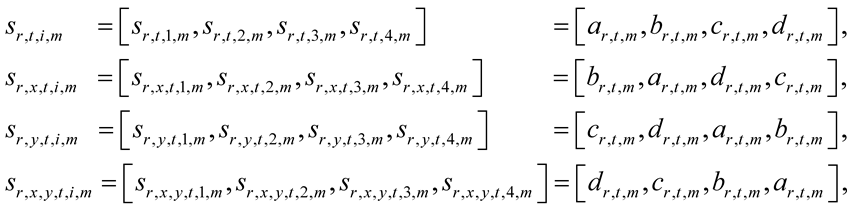(12)

where a_r,t,m, b_r,t,m, c_r,t,m, d_r,t,m are the eRSK_t structures.

The tRSK_t structures are [1, 4, M, 1] arrays, as well, which are represented in terms of 1 ´ 4 rows of the eRSK_t structures (12) and M ´ 4 matrices, e.g.,

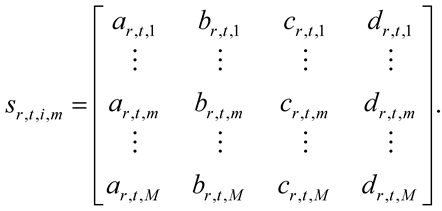(13)

Parallel to (3), the eRSK_t structures take the following form:

(14)

where functional amplitudes

(15)

are the first derivatives of (4). Along with (4) and (11), functional amplitudes (15) are smooth random functions of time from C^∞.

Together with the eRSK structures, the eRSK_t structures are [M, 1] arrays, which are exposed as M ´ 1 columns, such as

(16)

2.3. Differentiation Tables

Computing first spatial derivatives of the eRSK functions (7)-(11) gives the following differentiation table:

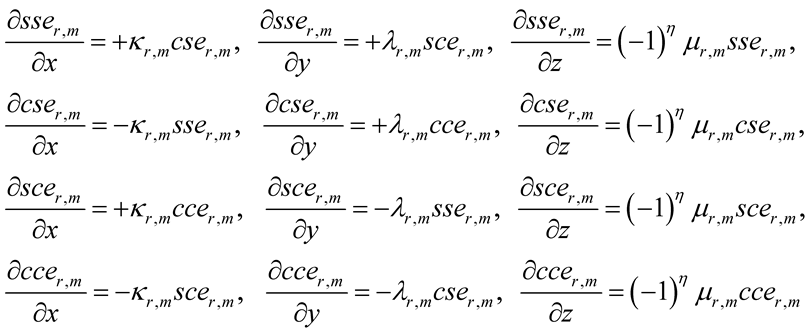(17)

that shows completeness of the eRSK functions with respect to differentiation in (x, y, z) of any order.

In agreement with differentiation table (17), the first derivatives of eRSK functions in x and y are covariant since they are proportional to eRSK cofunctions in the x- and y-directions, respectively. The first derivatives with respect to z are invariant because they are proportional to themselves.

It is a straightforward matter to show completeness of the eRSK structures (3)-(4) with respect to differentiation in (x, y, z) of any order for the reason that a table of first spatial derivatives becomes

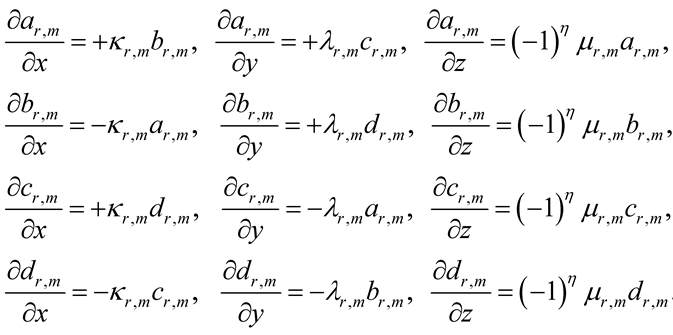(18)

In accordance with differentiation table (18), the first derivatives of the eRSK structures in x and y are covariant as they are proportional to eRSK costructures in the x- and y-directions, correspondingly. The first derivatives of the eRSK structures with respect to z are invariant.

Similarly, completeness of the eRSK_t structures (14)-(15) with respect to spatial differentiation of any order follows from the following table of first spatial derivatives:

(19)

Due to (19), the first derivatives of the eRSK_t in x and y are also covariant because they are proportional to eRSK_t costructures in the x- and y-directions, respectively. The first derivatives of the eRSK_t structures with respect to z are invariant.

A differentiation table of the tRSK structures (1) in x, y, and z turns out to be

(20)

where sign parameters

(21)

A set of first spatial derivatives of each tRSK structure in the x-, y-, and z-directions for i = 1, 2, ¼, I is equivalent to the differentiation table of eRSK structures (18). Similar to [1] , we observe quadrality of the theory: there are four equivalent theoretical ways of explaining the experimental results. It may be shown that the quadrality of the tRSK structures holds with respect to the second spatial derivatives, the Laplacian, and the first temporal derivative, as well. For the aim of brevity, further theoretical results will be demonstrated mainly for the tRSK structure s_r,i,m that is sufficient to describe experimental results.

Analogous to the eRSK structures, the first derivatives of the tRSK structures in x and y are covariant since they are proportional to tRSK costructures in the x- and y-directions, correspondingly. The first derivatives of the tRSK structures with respect to z are invariant.

Computation of a differentiation table of the tRSK_t structures (12) in x, y, and z yields

(22)

Alike the tRSK structures, a set of first spatial derivatives of each tRSK_t structure in the x-, y-, and z-directions for i = 1, 2, ¼, I is equivalent to the differentiation table of eRSK_t structures (19). So, differentiation tables (22) and (19) again show quadrality of the theory. For the aim of simplicity, further theoretical results will be displayed mainly for the tRSK_t structure s_r,t,i,m that is enough for generalization of experimental results.

Analogous to the eRSK_t structures (19) and the tRSK structures (20), the first derivatives of the tRSK_t structures in x and y are covariant as they are proportional to tRSK_t costructures in the x- and y-directions. The first derivatives of the tRSK_t structures with respect to z are invariant.

Similarity of differentiation tables (17), (18), (19), (20), (22) is visualized in terms of a differentiation diagram in Figure 1. The differentiation diagram demonstrates transformation of the eRSK functions, the eRSK structures, the eRSK_t structures, the tRSK structures, the tRSK_t structures, the eRVK structures, and the tRVK structures (see Section 3) produced by spatial differentiation that is shown with the help of blue arrows for derivatives in x, green arrows for derivatives

Figure 1. A differentiation diagram of the first spatial derivatives of the eRSK functions and the eRSK, eRSK_t, tRSK, tRSK_t, eRVK, and tRVK structures.

in y, and red arrows for derivatives in z. The length of arrows visualizing derivatives in x, y, and z are proportional to differentiation scales κ_r,m, λ_r,m, and (−1)^ημ_r,m, respectively, which are shown with colors corresponding to those of arrows.

Differentiation in x, y, and (x, y) moves elements of a given list of a random function and random structures

from one corner of the differentiation rectangle to another one, while differentiation in z does not change a location of elements of the given list. For the given list of the random function and the random structures, there are three lists of a random cofunction and random costructures. First, a list of the random cofunction and the random costructures in the x-direction

which are located on the same horizontal leg as the elements of the given list at a distance κ_r,m. Second, a list of the random cofunction and the random costructures in the y-direction

which are located on the same vertical leg as the elements of the given list at a distance λ_r,m. Third, a list of the random cofunction and the random costructures in the (x, y)-direction

which are located in the opposite corners with respect to the elements of the given list.

With the help of table (20) of the first spatial derivatives of the tRSK structures, we find second spatial derivatives of the tRSK structure s_r,i,m in x, y, and z

(23)

The differentiation diagram in Figure 1 clearly explains invariance of the repeated second spatial derivatives. The second-order differentiation moves the tRSK structure from a corner to an adjacent corner of the differentiation rectangle, transforming it into the tRSK costructure, and then returns the tRSK costructure back both in the x- and y-directions, restoring the original tRSK structure. Similar to physical oscillation, this effect of differentiation is called the scalar structural oscillation [1] of the tRSK structures.

In line with the differentiation diagram, the second derivative of the tRSK structure in (x, y) becomes the tRSK costructure covariant in (x, y), which is located at an opposite vertex of the differentiation rectangle to that of the original tRSK structure. The second derivatives of the tRSK structure in (x, z) and (y, z) become the tRSK costructures in the x- and y-directions, respectively, since differentiation in z is invariant.

Summation of the repeated second derivatives of (23) gives that the tRSK structure s_r,i,m and the eRSK structures are harmonic as

(24)

due to (10).

Using definitions (9), (11) and the spatial derivatives (20), we compute a first temporal derivative

(25)

where time-dependent amplitudes

(26)

So, the first temporal derivative of the tRSK and eRSK structures is a superposition of the tRSK and eRSK costructures in x, y, and t, while the time-dependent amplitudes depend on temporal derivatives of U_r,m, V_r,m, X_r,m,0, and Y_r,m,0. The tRSK, tRSK_t and eRSK, eRSK_t structures are closed with respect to temporal differentiation of the first order.

If

(27)

where U_d,m, V_d,m, X_d,m,0, and Y_d,m,0 are correspondent deterministic values, then the temporal derivative of the tRSK structure (25)-(26) is reduced to the temporal derivative of the tDSK structure (19) of [1] .

3. Random Vector Kinematic Structures

3.1. Definitions of the eRVK and tRVK Structures

Analogous to the eDVK structures (20) of [1] , the eRVK structures a_r,m, b_r,m, c_r,m, d_r,m are defined as gradients of the eRSK structures a_r,m, b_r,m, c_r,m, d_r,m, respectively, by

(28)

The eRVK structures are [3, 1, M, 1] arrays, which are visualized by 3 × 1 columns (28) of the eRSK structures multiplied by coefficients. Therefore, elements of columns (28) are [M, 1] arrays that are displayed by M × 1 columns (6).

Consequently, the tRVK structures are introduced as follows:

(29)

Equations (29) yield a row definition of the tRVK structures.

With the help of the definition of gradient and the first spatial derivatives of the tRSK structures (20), we obtain definitions of the tRVK structures in the column form. For the tRVK structure s_r,i,m, we have

(30)

Expansions (1) of the tRSK structures s_r,x,i,m, s_r,y,i,m, s_r,i,m for i = 1, 2, 3, 4 give the following matrix definition of the tRVK structure s_r,i,m:

(31)

Since substitution of the eRVK structures in the column form (28) into the row definition of the tRVK structure s_r,i,m (29) results in the same matrix (31), the first of four-dimensional (4-d) row definitions (29) is equivalent to the three-dimensional (3-d) column definition (30). Therefore, s_r,i,m is a [3, 4, M, 1] array, which is visualized by 3 × 4 matrix (31) of the eRSK structures multiplied by coefficients. Thus, elements of matrix (31) are [M, 1] arrays that are represented via M × 1 columns (6).

3.2. Definitions of the eRVK_t and tRVK_t Structures

Following (28), the eRVK_t structures a_r,t,m, b_r,t,m, c_r,t,m, d_r,t,m are defined as gradients of the eRSK_t structures a_r,t,m, b_r,t,m, c_r,t,m, d_r,t,m, correspondingly, in the following column form:

(32)

The eRVK_t structures are also [3, 1, M, 1] arrays, which are displayed by means of 3 × 1 columns (32) of the eRSK_t structures multiplied by coefficients. Elements of columns (32) are [M, 1] arrays that are visualized through M × 1 columns (16).

Accordingly, the tRVK_t structures are set in the row form by

(33)

The column form of the tRVK_t structures follows from the first spatial derivatives of the tRSK_t structures (22). For the tRVK_t structure s_r,t,i,m, we get

(34)

With the help of (12), the matrix form of s_r,t,i,m becomes

(35)

So, s_r,t,i,m is a [3, 4, M, 1] array, as well, which is exposed as 3 × 4 matrix (35) of the eRSK_t structures multiplied by coefficients, whereas elements of matrix (35) are [M, 1] arrays that are displayed through M × 1 columns (16).

Definitions of the tRVK structures (29) and tRVK_t structures (33), which are similar to definitions of the tRSK structures (1) and tRSK_t structures (12), again stipulate quadrality of theoretical formulas. Quadrality of the tRVK and tRVK_t structures is also confirmed by tables of the divergence, the curl, the first spatial derivatives, the second spatial derivatives, the Laplacian, and the first temporal derivative. For the purpose of conciseness, further theoretical results will be shown mostly for the tRVK structure s_r,i,m and the tRVK_t structure s_r,t,i,m that are sufficient for explanation of experimental results.

3.3. Differentiation Tables

Calculation of the divergence of the tRVK structure s_r,i,m with the help of (24)

(36)

shows that s_r,i,m and eRVK structures are divergence-free because of (10).

Using definitions of the curl of the tRVK structures (29) and the first spatial derivatives (20) of the tRSK structures, we find that the tRVK structures together with the eRVK structures are irrotational due to the commutativity of the second spatial derivatives of the tRSK structures. Namely, for s_r,i,m, we obtain

(37)

A tedious but straightforward computation of the differentiation table of the tRVK structures using both the column definition (34) and the row definition (33) yields

(38)

Therefore, differentiation table (38) of the tRVK structures is similar to differentiation table (20) of the tRSK structures since the differentiation tables of the scalar and vector structures become identical after substituting

(39)

This property of the tRSK, tRVK and eRSK, eRVK structures is called the scalar-vector invariance [1] of the theoretical and experimental invariant structures. The scalar-vector invariance is also illustrated by the differentiation diagram in Figure 1. The scalar-vector invariance holds for the second spatial derivatives, the Laplacian, and the first temporal derivative, as well.

Explicitly, a differentiation table of the second spatial derivatives of the tRVK structure s_r,i,m, which have been computed with the help of both the column definition (34) and the row definition (33),

(40)

resembles differentiation table (23). In agreement with the differentiation diagram in Figure 1, the repeated second spatial derivatives of the tRVK structure s_r,i,m and the eRVK structures are invariant and the mixed second spatial derivatives are covariant, what is consistent with the second spatial derivatives of the tRSK structure s_r,i,m and the eRSK structures.

Harmonicity of the tRVK structures and the eRVK structures immediately follows after summation of the repeated second spatial derivatives of (40). Alternatively, the column definition of the tRVK structure s_r,i,m (30) and harmonicity of the tRSK structures return a column Laplacian of s_r,i,m in the following form:

(41)

Eventually, we compute a first temporal derivative of s_r,i,m in the column form as

(42)

where the time-dependent amplitudes X_r,t,m and Y_r,t,m are provided by (26). The first temporal derivative of any tRVK structure is a superposition of the tRVK costructures in x, y, and t.

The tRVK structures and the eRVK structures are closed regarding spatial differentiation in (x, y, z) of any order due to (38). Completeness of the tRVK structure s_r,i,m and the tRVK_t structure s_r,t,i,m and the eRVK and eRVK_t structures with respect to temporal differentiation of the first order follows from (42).

4. Random Scalar Dynamic Structures

4.1. Definitions of the eRRSD and tRRSD Structures

We define the eRRSD structures as all kinds of products of the eRSK structures of the mth family a_r,m, b_r,m, c_r,m, d_r,m and the nth family a_r,n, b_r,n, c_r,n, d_r,n with wave indices m = 1, 2, ..., M and n = 1, 2, ..., M:

(43)

The eRRSD structures are closed since they include all possible products of the eRSK structures of the mth and nth families. The eRRSD structures (43) are [M, M] arrays, which are visualized by M × M matrices. For instance,

(44)

Consequently, the tRRSD structures are set via all kinds of products of the tRSK structures of the [i, m] family s_r,i,m, s_r,x,i,m, s_r,y,i,m, s_r,x,y,i,m and the [j, n] family s_r,j,n, s_r,x,j,n, s_r,y,j,n, s_r,x,y,j,n

(45)

where the indices of wave groups i = 1, 2, ..., I and j = 1, 2, ..., I and the indices of internal waves m = 1, 2, ..., M and n = 1, 2, ..., M.

The tRRSD structures are closed since they include all possible products of the tRSK structures of the [i, m] and [j, n] families. Due to quadrality of the tRSK structures, it is sufficient to consider s_r,i,ms_r,j,n to explain formulas for all eRRSD structures as

(46)

The tRRSD structure s_r,i,ms_r,j,n is a [4, 4, M, M] array, which is represented via 4 × 4 matrix (46) of the eRRSD structures. Elements of matrix (46) are the [M, M] arrays (44) that are exposed as M × M matrices. Other tRRSD structures are also 4 × 4 matrices of the eRRSD structures listed in various orders.

4.2. Differentiation Tables

Taking the first spatial derivatives of s_r,i,ms_r,j,n, substituting the first spatial derivatives of the tRSK structures (20), and using (20) with substitution [i = j, m = n] gives

(47)

Expansion of (47) in all group and wave indices demonstrates completeness of the eRRSD structures with respect to spatial differentiation of any order. The first derivative of the tRRSD structure s_r,i,ms_r,j,n and the eRRSD structures with respect to z is invariant and with respect to x and y is covariant.

We then take repeated second derivatives of (47) and substitute the first derivatives (20) and the repeated second spatial derivatives of (23) to obtain the repeated second derivatives of s_r,i,ms_r,j,n as follows:

(48)

Similar to the eRRSD structures, the repeated second derivatives of the tRRSD structure s_r,i,ms_r,j,n in x and y are partially invariant and the repeated second derivative in z is completely invariant.

Summation of (48) and simplification with the help of (10) return the Laplacian of the tRRSD structure in the following form:

(49)

Comparison of the dot product of the tRVK structures of the [i, m] and [j, n] families

(50)

with (49) yields

(51)

So, anhramonicity of the tRRSD structure s_r,i,ms_r,j,n and the eRRSD structures is stipulated by non-orthogonality of tRVK structures of the [i, m] and [j, n] families and the eRVK structures of the mth and nth families, respectively.

Theoretical Equations (47)-(51) for s_r,i,ms_r,j,n have been verified by differentiation tables of the eRRSD structures using the experimental and theoretical programming in Maple, while each theoretical formula corresponds to a table of 16 experimental formulas. Maple codes will be published elsewhere.

5. Random Vector Dynamic Structures

5.1. Definitions of the eRRVD and tRRVD Structures

The eRRVD structures of the mth family are defined alike (40) of [1] as all kinds of products of the eRVK structures of the mth family a_r,m, b_r,m, c_r,m, d_r,m and the eRSK structures of the nth family a_r,n, b_r,n, c_r,n, d_r,n with wave indices m = 1, 2, ..., M and n = 1, 2, ..., M:

(52)

Since the eRVK structures are computed as gradients (28) of the eRSK structures, the eRRVD structures a_r,ma_r,n, a_r,mb_r,n, a_r,mc_r,n, a_r,md_r,n, etc. are visualized by the following columns:

(53)

Thus, the eRRVD structures of the mth family are [3, 1, M, M] arrays, which are manifested via 3 × 1 columns (53) of the eRRSD structures multiplied by coefficients, where elements of columns (53) are [M, M] arrays that are exposed as M × M matrices, which are analogous to matrix (44).

Consequently, the eRRVD structures of the nth family are set as all kinds of products of the eRSK structures of the mth family a_r,m, b_r,m, c_r,m, d_r,m and the eRVK structures of the nth family a_r,n, b_r,n, c_r,n, d_r,n with wave indices m = 1, 2, ..., M and n = 1, 2, ..., M:

(54)

The eRRVD structures of the mth and nth families are closed since they include all possible products of the eRSK and eRVK structures of the mth and nth families.

As the eRVK structures are gradients of the correspondent eRSK structures, the eRRVD structures a_r,ma_r,n, a_r,mb_r,n, a_r,mc_r,n, a_r,md_r,n, etc. are displayed by the following columns:

(55)

So, the eRRVD structures of the nth family are also the [3, 1, M, M] arrays, which are exposed via 3 × 1 columns (55) of the eRRSD structures multiplied by coefficients, where elements of columns (55) are [M, M] arrays that are represented in terms of M × M matrices, like (44).

We then introduce the tRRVD structures of the mth family as all kinds of products of the tRVK structures (29) of the [i, m] family and the tRSK structures (1) of the [j, n] family. Namely,

(56)

where i = 1, 2, ..., I and j = 1, 2, ..., I are the indices of wave groups and m = 1, 2, ..., M and n = 1, 2, ..., M are the indices of internal waves.

Due to quadrality of the tRSK and tRVK structures, it is sufficient to consider the tRRVD structure of the mth family s_r,i,ms_r,j,n to explain formulas for all eRRSD structures of the mth family (52) as

(57)

The tRRVD structure of the mth family s_r,i,ms_r,j,n is a [4, 4, 3, 1, M, M] array that is represented in terms of 4 × 4 matrix (57) of the eRRVD structures of the mth family. Elements of matrix (57) are displayed as the [3, 1, M, M] arrays that are visualized via 3 × 1 columns (53) of M × M matrices of the eRRSD structures (44) multiplied by coefficients. Other tRRVD structures of the mth family are 4 × 4 matrices of the eRRVD structures of the mth family arranged in different orders.

The tRRVD of the nth family are set as all kinds of products of the tRSK structures of the [i, m] family and the tRVK structures of the [j, n] family. Explicitly,

(58)

where i = 1, 2, ..., I and j = 1, 2, ..., I are the group indices and m = 1, 2, ..., M and n = 1, 2, ..., M are the wave indices.

The tRRVD structures of the mth and nth families are closed since they include all possible products of the tRVK and tRSK structures of the [i, m] and [j, n] families. Because of quadrality of the tRSK and tRVK structures, it is enough to consider the tRRVD structure of the nth family s_r,i,ms_r,j,n to generalize formulas for all eRRSD structures of the nth family (54) since

(59)

The tRRVD structure of the nth family s_r,i,ms_r,j,n is the [4, 4, 3, 1, M, M] array that is visualized by 4 × 4 matrix (59) of the eRRVD structures of the nth family. Elements of matrix (59) are again the [3, 1, M, M] arrays that are displayed via 3 × 1 columns (55) of M × M matrices of the eRRSD structures multiplied by coefficients. Other tRRVD structures of the nth family are 4 × 4 matrices of the eRRVD structures of the nth family listed in various orders.

5.2. The Helmholtz Decomposition of the Directional Derivatives

Substitution of the first spatial derivatives of the tRSK (20) and tRVK (38) structures in the vector definitions (42) of [1] of the derivative of the tRVK structure s_r,j,n in the direction of the tRVK structure s_r,j,m and the derivative of the tRVK structure s_r,j,m in the direction of the tRVK structure s_r,j,n and simplification yield the directional derivatives in the following vector form:

(60)

We then sum up and subtract the directional derivatives (60) to find an anticommutator and a commutator of the tRVK structures s_r,i,m and s_r,j,n via the tRRVD structures of the nth and mth families as

(61)

(62)

Verification of the directional derivatives (60), the anticommutator (61), and the commutator (62) in terms of eRRDV structures shows that each theoretical formula via the tRVK structures and the tRRVD structures corresponds to a table of 16 formulas in the eRVK and eRRVD structures and demonstrates completeness of the eRRVD structures with respect to the directional derivatives, the anticommutator, and the commutator.

Above computations (60)-(62) in the component form, which are straightforward but too tedious to be shown in this paper, have been also implemented with the help (44) of [1] . Comparison of the gradient of the dot product of the RVK structures s_r,i,m and s_r,j,n that has been implemented using (49) of [1] with the anticommutator (61) in the component form yields

(63)

Using (55) of [1] , we similarly compute the curl of the cross product of the RVK structures s_r,i,m and s_r,j,n in the component form and compare the curl with the component form of the commutator (62) to find that

(64)

Computations of (63) and (64) via the component form prove that the gradient of the dot product of the tRVK structures and the curl of the cross product of the tRVK structures s_r,i,m and s_r,j,n are expandable through the eRRSD structures (43) and the tRRSD structures (45) and component decompositions in the tRRSD and eRRSD structures completely match each other.

Solving the vector expansions (63) and (64) with respect to the directional derivatives yields

(65)

In agreement with the Fundamental Theorem of Vector Analysis [7] , a vector field of the directional derivatives may be decomposed into the gradient of a scalar Helmholtz potential and the curl of a vector Helmholtz potential as follows:

(66)

where the scalar Helmholtz potential is symmetric because

(67)

and the vector Helmholtz potential is asymmetric since

(68)

So, the scalar Helmholtz potential equals to a positive half of the dot product of the tRVK structures s_r,i,m and s_r,j,n and the vector Helmholtz potential is equal to a negative half of the cross product of the tRVK structures s_r,i,m and s_r,j,n.

Finally, we compute the gradient of the tRRSD structure s_r,i,ms_r,j,n by the vector product rule and substitute definitions of the tRVK structures (29) and the tRRVD structures (56) and (58) to obtain

(69)

Thus, the gradient of a tRRSD structure may be decomposed into the sum of correspondent tRRVD structures of the nth and mth families.

6. The Random Stokes Field

6.1. The Helmholtz Decomposition of the Navier-Stokes Equations

Random internal waves of a Newtonian fluid with a constant density ρ_c and a constant dynamic viscosity μ_c in a field of gravity g = [g_x, g_y, g_z] are governed by the momentum conservation law [8] [9]

(70)

and the mass conservation law

(71)

where

(72)

is a velocity field of a random flow,

(73)

is a cumulative pressure of the random flow. The quasi-scalar Dirichlet problem for the Navier-Stokes Equations (70)-(71) may be set on the upper and lower boundaries of the upper domain

(74)

for u_r,z by

(75)

and on the upper and lower boundaries of the lower domain

(76)

via

(77)

where

(78)

is a random boundary function, which will be treated in Section 6.3. Configuration of the upper and lower domains of internal waves is shown in Figure 2 of [1] . In agreement with boundary conditions (75), (77), the internal waves are produced by surface waves propagating in a generation domain.

From the viewpoint of the Fundamental Theorem of Vector Analysis [7] , the quasi-scalar Dirichlet problem (74)-(78) for the random Navier-Stokes equations (70)-(71) in vector and scalar variables (72)-(73) may be treated as a problem of construction of the Helmholtz decomposition for the Archimedean field

(79)

the random Stokes field

(80)

and the random Navier field

(81)

The Archimedean, the random Stokes, and the random Navier fields are decomposed using the scalar Helmholtz potentials p_A, p_S,r, and p_N,r, respectively, as follows:

(82)

where p_A stands for the hydrostatic pressure of the Archimedean problem, p_S,r for the kinematic pressure of the random Stokes problem, and p_N,r for the dynamic pressure of the random Navier problem.

Summation of (79)-(81) and (82) yield the Helmholtz decomposition of the random Navier-Stokes equation (70)

(83)

where a cumulative pressure of the random flow p_c,r is a scalar Helmholtz potential of the sum of the Archimedean, the random Stokes, and the random Navier fields.

The problem of finding the scalar Helmholtz potential p_A of the Archimedean field F_A has a general solution [8] [9]

(84)

where p₀(t) is a reference pressure, which is a smooth function of time from C^∞.

A problem of calculating the velocity field u_r, which is subjected to the boundary conditions (74)-(78), and the scalar Helmholtz potential p_S,r of the random Stokes field F_S,r becomes:

(85)

(86)

It will be called afterwards the random Stokes problem. Contrary to the classical Stokes equations that are treated for small Reynolds numbers, the random Stokes problem (85)-(86), (74)-(78) is set for all Reynolds numbers.

A problem of computing the scalar Helmholtz potential p_N,r of the random Navier field F_N,r for the velocity field u_r, which is given by a solution of (85)-(86), (74)-(78),

(87)

will be later referred to as the random Navier problem. Since we are looking for an exact solution of the Dirichlet problem (70)-(78), the random Navier problem is set for all Reynolds numbers, as well.

6.2. The Random Stokes Problem

A general wave solution of the random Stokes problem (85)-(86) is

(88)

(89)

where φ_u,r is the scalar Helmholtz potential of the random velocity field that should be harmonic, i.e.

(90)

and the temporal derivative of φ_u,r should commutate with the gradient.

The random velocity field u_r is formed by velocity fields u_r,i of I wave groups with M internal waves per group. Thus,

(91)

Because of the quadrality of the tRVK structures, we use the simplest tRVK structure s_r,i,m to expand the velocity fields of I wave groups as follows:

(92)

for i = 1, 2, ..., I.

Combining (91)-(92) and changing the order of summation yields

(93)

Using definition (29) of the tRVK structures via the tRSK structures, we get

(94)

In agreement with the Helmholtz decomposition of the velocity field (88), the scalar Helmholtz potential represented in terms of the tRSK structure s_r,i,m takes the following form:

(95)

Indeed, the Laplace equation (90) is satisfied identically since s_r,i,m is harmonic (24).

We then substitute the velocity potential (95) in (89) and use the temporal derivative of s_r,i,m (25) to find the kinematic pressure of the random Stokes problem that is expanded in the tRSK structures s_r,x,i,m, s_r,y,i,m and the the tRSK_t structure s_r,t,i,m as follows:

(96)

To verify the general solution (93), (96) of the random Stokes problem (85)-(86) in the the tRVK, tRSK, and tRSK_t structures, we use the temporary derivative of the tRVK structure s_r,i,m (42) to find

(97)

Since the tRVK structure s_r,i,m is harmonic (41),

(98)

Computing the gradient of p_S,r with the help of gradient of the tRSK structures s_r,x,i,m, s_r,y,i,m (29) and of the tRSK_t structure s_r,t,i,m (33) gives

(99)

Substitution of Equations (97)-(99) in the momentum conservation law (85) of the random Stokes problem shows that it is satisfied identically. Because the tRVK structure s_r,i,m is divergence-free (36), the mass conservation law (86) of the random Stokes problem is fulfilled identically, as well.

6.3. The Random Boundary Function

To find an admissible form of the random boundary function (78), we compute a general solution for a z-component u_r,z of the random velocity field. In agreement with (88), (95), (20), and (10),

(100)

Similar to the 3-v tRSK structure s_r,i,m = [a_r,m, b_r,m, c_r,m, d_r,m](X_r,m, Y_r,m, z) (1), define a two-variables (2-v) tRSK boundary structure

(101)

where [a_b,r,m, b_b,r,m, c_b,r,m, d_b,r,m](X_b,r,m, Y_b,r,m) are the 2-v eRSK boundary structures, which are set up as follows:

(102)

Here, m = 1, 2, ..., M is a counter of random boundary waves, M is a number of boundary waves per wave group,

(103)

are random boundary amplitudes of a harmonic variable v(x, y, z, t).

The 2-v eRSK boundary functions [ss_b,r,m, cs_b,r,m, sc_b,r,m, cc_b,r,m](X_b,r,m, Y_b,r,m) are products

(104)

of the 1-v eRSK boundary functions [sx_b,r,m, cx_b,r,m](X_b,r,m) and [sy_b,r,m, cy_b,r,m](Y_b,r,m):

(105)

where X_b,r,m = X_b,r,m(x, t) and Y_b,r,m = Y_b,r,m(y, t) are boundary propagation variables defined by

(106)

In Equations (101)-(106), [X_b,r,m, Y_b,r,m] is the Cartesian coordinate of a frame of reference moving with the mth random boundary wave, [U_b,r,m, V_b,r,m] is a boundary celerity of propagation, [X_b,r,m,0, Y_b,r,m,0] is a reference value of [X_b,r,m, Y_b,r,m] at t = 0, x = 0, y = 0, and parameters

(107)

together with (103) are smooth random functions of time from C^∞. The wave numbers κ_b,r,m and λ_b,r,m are constants.

In terms of the tRSK boundary structure s_b,r,i,m (101), the random boundary function

(108)

If and only if

(109)

then the Cartesian coordinate of the moving frame, the 1-v eRSK functions, the 3-v eRSK functions, the 3-v eRSK structures, and the 3-v tRSK structure s_r,i,m are related with the correspondent boundary variables as follows:

(110)

and the Dirichlet boundary conditions of (74)-(78)

(111)

are fulfilled exactly for U and L. The conditions at infinities of (74)-(78) are also satisfied since ez_r,m(z) represents the decay model both for U and L due to the sign parameter η.

7. The Random Navier Field

7.1. Expansion of the Random Navier Field

For the random Navier field F_N,r (81), the random Navier problem (82) of computing the scalar Helmholtz potential p_N,r of F_N,r is reduced to solving of the random Navier equation (87).

The random velocity field u_r is a superposition (91) of the velocity fields of I wave groups

(112)

In agreement with (92), velocity fields u_r,i and u_r,j are expanded in the tRVK structures s_r,i,m, s_r,i,n, s_r,j,m, s_r,j,n as follows:

(113)

Combining (112) and (113) yields four equivalent presentations of the random velocity field

(114)

i.e. quadrality of the of the random velocity field.

Substitution of the group decomposition (112) in the Navier field (81), expansion of the dot product of u_r and ∇, and reduction of the product of two one-dimensional (1-d) sums to a two-dimensional (2-d) sum by

(115)

yield

(116)

We then reduce the rectangular summation to the diagonal and triangular summations using (89) of [4]

(117)

to find a decomposition of F_N,r into two Navier fields

(118)

First, the diagonal (j = i) Navier field F_N,g,r,i,r,i of interaction of I selfsame random wave groups

(119)

where F_N,r,i,r,i is the Navier field of diagonal interaction of the selfsame ith random wave group, which is given by the half-anticommutator of [u_r,i, u_r,i] for i = 1, 2, ..., I.

Second, the non-diagonal (j > i) Navier field F_N,g,r,i,r,j of interaction between I(I − 1)/2 distinct random wave groups

(120)

where F_N,r,i,r,j is the Navier field of non-diagonal interaction between the distinct ith and jth random wave groups, which is expressed via the anticommutator of [u_r,i, u_r,j] for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I.

We then substitute the decomposition of the velocity field u_r,i (113) of the ith wave group via the tRVK structures in (119), expand the dot product of u_r,i and ∇, and combine the product of 1-d sums into a 2-d sum to get the following rectangular expansion:

(121)

To use Equation (117) in the case of rectangular summation in waves (121), we substitute in (117) i = m, j = n, I = M to find

(122)

where the first general term A_r,mB_r,m sums up elements of the diagonal summation matrix, the second general term A_r,mB_r,n sums up by rows elements of the upper triangular summation matrix, and the third general term A_r,nB_r,m sums up by columns elements of the lower triangular summation matrix.

Using (122) for the rectangular sum (121) yields that the random Navier field F_N,r,i,r,i (119) of diagonal interaction of the selfsame ith wave group is expanded in two sums:

(123)

First, the internal (n = m) sum of the random Navier field F_{N,r,i,m,r,i,m} of propagation of the mth wave from the selfsame ith wave group

(124)

which is represented via the half-anticommutator of the tRVK structures [s_r,i,m, s_r,i,m] for i = 1, 2, ..., I and m = 1, 2, ..., M.

Second, the external (n > m) sum of the Navier field F_{N,r,i,m,r,i,n} of diagonal interaction between the distinct mth and nth waves from the selfsame ith wave group

(125)

which is described by the anticommutator of the tRVK structures [s_r,i,m, s_r,i,n] for i = 1, 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

Substituting in (120) the expansions of the velocity fields u_r,i and u_r,j (113) of the ith and jth wave groups in terms of the tRVK structures and simplifying analogously to (121) return the following rectangular expansion:

(126)

Reduction of the rectangular sum (126) with the help of (122) gives that the random Navier field F_N,r,i,r,j (120) of non-diagonal interaction between the distinct ith and jth wave groups may be also decomposed in two sums as follows:

(127)

Primarily, the internal sum of the Navier field F_{N,r,i,m,r,j,m} of non-diagonal interaction between the mth waves from the distinct ith and jth wave groups

(128)

which is represented in terms of the anticommutator of the tRVK structures [s_r,i,m, s_r,j,m] for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, and m = 1, 2, ..., M.

Secondly, the external sum of the random Navier field F_{N,r,i,m,r,j,n} of non-diagonal interaction between the distinct mth and nth waves from the distinct ith and jth wave groups

(129)

which is given by two anticommutators of the tRVK structures [s_r,i,m, s_r,j,n] and [s_r,i,n, s_r,j,m] for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

7.2. Potentialization of the Random Navier Field

The Navier fields F_{N,r,i,m,r,i,m} (124) and F_{N,r,i,m,r,i,n} (125) and may be converted into the potential form with the help of the Helmholtz decomposition (65) of the derivative of s_r,i,m in the direction of s_r,i,m, the derivative of s_r,i,n in the direction of s_r,i,m, and the derivative of s_r,i,m in the direction of s_r,i,n, namely,

(130)

Computation of the anticommutator

(131)

results in cancellation of the vector Helmholtz potentials and potentialization of the anticommutator of [s_r,i,m, s_r,i,n].

Substituting anticommutators (130)-(131) in F_N,r,i,r,i (123)-(125) and pulling out the gradient operator give

(132)

Similarly, the Helmholtz decomposition (65) of the derivative of s_r,j,m in the direction of s_r,i,m, the derivative of s_r,i,m in the direction of s_r,j,m, the derivative of s_r,j,n in the direction of s_r,i,m, the derivative of s_r,i,m in the direction of s_r,j,n, the derivative of s_r,j,m in the direction of s_r,i,n, and the derivative of s_r,i,n in the direction of s_r,j,m are following:

(133)

We then compute three anticommutators

(134)

and again observe results cancellation of the vector Helmholtz potentials and potentialization of the anticommutators of [s_r,i,m, s_r,j,m], [s_r,i,m, s_r,j,n], and [s_r,i,n, s_r,j,m].

Substituting anticommutators (134) in F_N,r,i,r,j (127)-(129) and pulling out the gradient operator yield

(135)

Eventually, we substitute (132) and (135) in (118)-(120), combine terms and pull out the gradient to show that the Navier field F_N,r (81) is potential since

(136)

Cancellation of the vector Helmholtz potentials correlates with the third Newton law since the vector Helmholtz potentials describe internal forces of interaction between the random waves. In agreement with the third Newton law, the internal forces have the same magnitudes and opposite directions. The scalar Helmholtz potentials describe external forces with a non-trivial resultant, which moves the random system in agreement with the second Newton law.

7.3. Reduction of the Random Navier Field

It is a straightforward but tedious matter to show that the orders of diagonal summations in i and m and triangular summations in (i, j) and (m, n) may be interchanged as follows:

(137)

(138)

(139)

(140)

With the help of (137)-(140), the Navier field (136) may be converted to

(141)

Using (117) and (122), we then compute the following inverse reductions of the diagonal and triangular summations to the rectangular summation:

(142)

(143)

(144)

(145)

To derive Equation (145), the general term A_r,m·A_r,n of sums of Equation (144) is replaced with the summation matrix of A_r,i,m·A_r,j,n in (i, j). Equation (145) is reduced to Equation (144) for I = 1. All theoretical relationships between the diagonal, triangular, and rectangular summations (115), (117), (122), (137)-(140), (142)-(145), (161) have been also justified experimentally.

Usage of (142) and (143) helps to eliminate the diagonal and triangular summations in (i, j) and transform (141) to

(146)

We then use (145) to reduce the diagonal and triangular summations in (m, n) and to conclude with a last form of the potentialized Navier field

(147)

Using the definition of the kinetic energy K_e,r and velocity expansions (112)-(114), we change the orders of summation to get the alternative presentations of K_e,r:

(148)

Comparison of (147) with (148) and (82) yields a relationship between the random Navier field and the kinetic energy

(149)

and the scalar Helmholtz potential of the random Navier field

(150)

7.4. The Pressure Field of the Random Navier-Stokes Problem

Substitution of the kinetic energy (148) in (150) gives the dynamic pressure

(151)

in terms of the tRVK structures. Substituting the dot products of the tRVK structures (50) yields p_N,r in terms of the tRRSD structures

(152)

Combining the scalar Helmholtz potentials of the Archimedean (84), the Stokes (96), and the Navier (152) fields returns the cumulative random pressure

(153)

in the tRSK, tRSK_t, and tRRSD structures.

Expressing the dot product of the tRVK structures via the Laplacian of the tRRSD structures (51)

(154)

substituting the dot product in Equation (151), and combining terms yield

(155)

Equation (155) demonstrates a mathematical meaning of the dynamic random pressure: −4p_N,r is a source of the stationary diffusion of the superposition of all tRRSD structures with a diffusion coefficient ρ_c.

7.5. Verification of the Random Navier-Stokes Problem

To verify the random solution (114) and (152) by (87), we use an expanded vector form of the directional derivative

(156)

In agreement with (114) and (29), the x-, y-, z-components of u_r are

(157)

and the random velocity field

(158)

Substitution of (157)-(158) in (156) and combining sums gives

(159)

We then substitute the spatial derivatives of the tRSK (20) and tRVK (38) structures and collect like terms to represent the directional derivative in terms of the tRRVD structures of the nth family as follows:

(160)

Application of a 4-d transposed summation for a superposition of the tRRVK structures with symmetric coefficients yields

(161)

Therefore, directional derivative (160) may be represented via the tRRVD structures of the mth and nth families in the following symmetric form:

(162)

Using (69), we then split the gradient ∇p_N,r of the dynamic random pressure (152) into two parts. In the first part named ∇_mp_N,r, terms including ∇[s_r,x,i,m, s_r,y,i,m, s_r,i,m] = [s_r,x,i,m, s_r,y,i,m, s_r,i,m] are collected. In the second part termed ∇_np_N,r, terms with ∇[s_r,x,j,n, s_r,y,j,n, s_r,j,n] = [s_r,x,j,n, s_r,y,j,n, s_r,j,n] are combined.

Namely,

(163)

where

(164)

is computed in terms of of the tRRVD structures of the mth family and

(165)

via the tRRVD structures of the nth family.

Finally, combining (162) and (163)-(165) yields that the random Navier PDE (87) is satisfied identically.

8. Decomposition of a Random Matrix of the Kinetic Energy

We proceed computation using for the kinetic energy K_e,r of the stochastic chaos of random internal waves sum (148) in wave groups, viz.

(166)

For clarification of summation, primarily, we define a random matrix of the kinetic energy M_e,r by

(167)

where the braces notation {M_e,r} denotes the rectangular summation of all elements of the summation matrix M_e,r for i =1, 2, ..., I and j =1, 2, ..., I.

Due to expansions in the tRVK structures (113), the summation matrix takes the following form:

(168)

where the summation braces {s_r,i,m·s_r,j,n} signify the rectangular summation of all elements of a summation matrix with the general term s_r,i,m·s_r,j,n for i =1, 2, ..., I, j =1, 2, ..., I. Hence, elements of summation matrix (168) are matrices of size M × M.

Second, we decompose M_e,r with the help of a generalization of (117) in random wave groups as follows:

(169)

where

(170)

is a diagonal matrix for i =1, 2, ..., I, which includes all diagonal elements of M_e,r and

(171)

is a complementary matrix for i = 1, 2, ..., I − 1 and j = i + 1, i + 2, ..., I, which is composed of the upper and lower triangular matrices of M_e,r.

The kinetic energy is correspondingly expanded as

(172)

where a first sum

(173)

is produced by the elements of M_e,r,d and a second sum

(174)

by the elements of M_e,r,u,l.

In (173)-(174), the general term of K_e,r,d is

(175)

for i = 1, 2, ..., I, m = 1, 2, ..., M, and n = 1, 2, ..., M and the general term of K_e,r,u,l is

(176)

for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, m = 1, 2, ..., M, and n = 1, 2, ..., M.

Third, in agreement with a generalization of (122), we expand all random rectangular sums into internal wave sums with n = m, which correspond to internal interaction of random elementary oscillons from the mth family (209)-(210), and external wave sums with n ≠ m, which describe external interaction of random elementary oscillons from the mth and nth families (see Section 13).

The summation matrix of the diagonal general term K_r,i,r,i (175) of K_e,r,d (173)

(177)

due to the commutative property of the dot products

(178)

yields the following reduction of the rectangular summation to the diagonal and triangular summations:

(179)

for i = 1, 2, ..., I.

The summation matrices of the non-diagonal general term K_r,i,r,j (176) of K_e,r,u,l (174)

(180)

because of the commutative properties of the dot products

(181)

produce the following reduction of the rectangular summation to the diagonal and triangular summations:

(182)

for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I. If j = i, the asymmetric reduction (182) is converted into the symmetric reduction (179).

9. Random Wave, Group, and Energy Pulsons of Propagation

The general term of internal sum of (179) produces a a random wave pulson of propagation (a random wave pulson for brevity)

(183)

which describes vector self-interaction of the velocity field s_r,i,m of the mth elementary oscillon (209)-(210) from the selfsame ith random wave group for i = 1, 2, ..., I and m = 1, 2, ..., M.

In the view of (30), the random wave pulson in the tRRSD structures takes the following form:

(184)

A superposition of a group of the random wave pulsons is termed a random group pulson

(185)

Here, K_{g,r,i,m,r,i,m} is simplified by the Pythagorean identity for the wave numbers (10) and the definitions of the eRSK structures (3) and the 3-v eRSK functions (7)-(8).

Eventually, the diagonal summation of all random group pulsons results in a random energy pulson

(186)

which shows a cumulative energy of M random group pulsons.

10. Random Wave, Group, and Energy Oscillons of Diagonal External Interaction

The general term of external sum of (179) generates a random wave oscillon of diagonal external interaction (a random diagonal wave oscillon for brevity)

(187)

which expresses vector external interaction of the velocity fields s_r,i,m and s_r,i,n of the distinct mth and nth elementary oscillons from the selfsame ith random wave group for i = 1, 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

Using (30) and Equation (30) with m = n, we obtain the random diagonal wave oscillon

(188)

via the tRRSD structures

Summation of (188) yields a random diagonal group oscillon in terms of the eRRSD structures

(189)

where a nonlinear amplitude

(190)

is produced by the wave numbers.

The triangular summation of the random diagonal group oscillons results in a random diagonal energy oscillon

(191)

which gives a cumulative energy of all random diagonal group oscillons.

So, summation of the diagonal constituents K_r,i,r,i (173) of the kinetic energy K_e,r,d is completed with the following result:

(192)

If n = m, then the random diagonal wave oscillon (188) is converted into the doubled wave pulson (184). Namely,

(193)

Analogously, the random diagonal group oscillon (189) becomes equal to the doubled random group pulson (185)

(194)

since

(195)

11. Random Wave, Group, and Energy Oscillons of Non-Diagonal Internal Interaction

The general term of internal sum of (182) yields a random wave oscillon of internal interaction (a random internal wave oscillon for brevity)

(196)

which represents vector internal interaction of the velocity fields s_r,i,m and s_r,j,m of the mth elementary oscillons from the distinct ith and jth random wave groups for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, and m = 1, 2, ..., M.

In the tRRSD structures, the random internal wave oscillon becomes

(197)

Adding the random internal wave oscillons, we get a random internal group oscillon via the eRRSD structures

(198)

The diagonal summation of the random internal group oscillon results in a random internal energy oscillon

(199)

which returns a cumulative energy of M random internal group oscillons.

12. Random Wave, Group, and Energy Oscillons of Non-Diagonal External Interaction

The general term of external sum of (182) describes a random wave oscillon of non-diagonal external interaction (a random external wave oscillon for brevity)

(200)

which exposes vector external interaction of the velocity fields s_r,i,m, s_r,j,n and s_r,j,m, s_r,i,n of the distinct mth and nth elementary oscillons from the distinct ith and jth random wave groups for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

In the same manner as (188), we compute the random external wave oscillon

(201)

via the tRRSD structures.

A random external group oscillon takes the following form in terms of the eRRSD structures:

(202)

where nonlinear amplitudes

(203)

are generated by the wave numbers.

We then imply the triangular summation of the random external group oscillons to find a random external energy oscillon

(204)

which demonstrates a cumulative energy of M(M − 1)/2 random external group oscillons.

Thus, summation of the non-diagonal constituents K_r,i,r,j (174) of the kinetic energy K_e,r,u,l for i =1, 2,..., I − 1 and j = i + 1, i + 2, ..., I is finished as follows:

(205)

If n = m, then the random external wave oscillon (201) is transformed into the doubled random internal wave oscillon (197). Explicitly,

(206)

Similarly, the random external group oscillon (202) becomes equal to the doubled random internal group oscillon (198), i.e.

(207)

because

(208)

13. Random Elementary Oscillons and Pulsons

The mth random elementary oscillon of propagation of the velocity potential s_r,i,m (the random elementary oscillon for brevity) from the selfsame ith random wave group is defined by

(209)

where i = 1, 2, ..., I and m = 1, 2, ..., M.

Explicitly, four random elementary oscillons of the mth family

(210)

are expressed via the eRSK structures (3).

A random wave oscillon

(211)

consists of I random elementary oscillons.

Similarly, a random group oscillon

(212)

is composed of M random wave oscillons.

In the tRRSD structures, a random elementary pulson of propagation (a random elementary pulson for brevity) is defined by

(213)

The random elementary pulson (213) describes scalar self-interaction of the velocity potential s_r,i,m of the selfsame mth elementary oscillon (209)-(210) from the selfsame ith random wave group for i = 1, 2, ..., I and m = 1, 2, ..., M.

In terms of the eRRSD structures, the random elementary pulsons become

(214)

The random wave pulsons (184) via the eRRSD structures take the following form:

(215)

The random wave pulsons (215) and the random group pulson (185) then become the following superpositions of the random elementary pulsons (214):

(216)

and

(217)

In the tRRSD structures, a random elementary oscillon of internal interaction (a random internal elementary oscillon for brevity) is specified by

(218)

The random internal elementary oscillon (218) represents scalar internal interaction of the velocity potentials s_r,i,m and s_r,j,m of the mth elementary oscillons from the distinct ith and jth random wave groups for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, and m = 1, 2, ..., M.

In terms of the eRRSD structures, there are six random internal elementary oscillons

(219)

The random internal wave oscillons (197) via the eRRSD structures may be written as follows:

(220)

The random internal wave oscillons (220) and the random internal group oscillon (198) are decomposed via the random internal elementary oscillons (219) as follows:

(221)

and

(222)

In the tRRSD structures, a random elementary oscillon of diagonal external interaction (a random diagonal elementary oscillon for brevity) is established by

(223)

The random diagonal elementary oscillon (223) manifests scalar external interaction of the velocity potentials s_r,i,m and s_r,i,n of the distinct mth and nth elementary oscillons from the selfsame ith random wave group for i = 1, 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

In terms of the eRRSD structures, there are four random diagonal elementary oscillons

(224)

The random diagonal wave oscillons (188) via the eRRSD structures become

(225)

The random diagonal wave oscillons (225) and the random diagonal group oscillon (189) then are subsequent superpositions of the random diagonal elementary oscillons (224):

(226)

and

(227)

In the tRRSD structures, a random elementary oscillon of non-diagonal external interaction (a random external elementary oscillon for brevity) is set by

(228)

The random external elementary oscillon (228) expresses scalar external interaction of the velocity potentials s_r,i,m, s_r,j,n and s_r,j,m, s_r,i,n of the distinct mth and nth elementary oscillons from the distinct ith and jth random wave groups for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

In terms of the eRRSD structures, there are six random external elementary oscillons

(229)

The random external wave oscillons (201) via the eRRSD structures may be represented in the following form:

(230)

The random external wave oscillons (230) and the random external group oscillon (202) are expanded in the random external elementary oscillons (229) in the following way:

(231)

and

(232)

If n = m, then the random diagonal elementary oscillons (223)-(224) are reduced to the doubled random elementary pulsons of propagation (213)-(214), i.e.

(233)

In the similar way, if n = m, then the random external elementary oscillons (228)-(229) are transformed into the doubled random internal elementary oscillons (218)-(219). Namely,

(234)

14. Conclusions

Finally, we summarize quantization of the kinetic energy of the stochastic chaos of exponential oscillons and pulsons. The random cumulative pulson of the kinetic energy (172) may be decomposed as follows:

(235)

where K_{e,r,i,m,r,i,m} is the random energy pulson (186), K_{e,r,i,m,r,j,m} is the random internal energy oscillon (199), K_{e,r,i,m,r,i,n} is the random diagonal energy oscillon (191), and K_{e,r,i,m,r,j,n} is the random external energy oscillon (204).

The random group pulson K_{g,r,i,m,r,i,m} (185) is composed of I random wave pulsons K_{w,r,i,m,r,i,m} (183) that describe vector self-interaction of the velocity field s_r,i,m of the mth elementary oscillon (209)-(210) from the selfsame ith random wave group for i = 1, 2, ..., I and m = 1, 2, ..., M.

The random internal group oscillon K_{g,r,i,m,r,j,m} (198) consists of I(I − 1)/2 random internal wave oscillons K_{w,r,i,m,r,j,m} (196) that represent vector internal interaction of the velocity fields s_r,i,m and s_r,j,m of the mth elementary oscillons from the distinct ith and jth random wave groups for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, and m = 1, 2, ..., M.

The random diagonal group oscillon K_{g,r,i,m,r,i,n} (189) is constructed of I random diagonal wave oscillons K_{w,r,i,m,r,i,n} (187) that express vector external interaction of the velocity fields s_r,i,m and s_r,i,n of the distinct mth and nth elementary oscillons from the selfsame ith random wave group for i = 1, 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

The random external group oscillon K_{g,r,i,m,r,j,n} (202) includes I(I − 1)/2 random external wave oscillons K_{w,r,i,m,r,j,n} (200) that expose vector external interaction of the velocity fields s_r,i,m, s_r,j,n and s_r,j,m, s_r,i,n of the distinct mth and nth elementary oscillons from the distinct ith and jth random wave groups for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

The random wave pulsons (184), (215) are composed of three of I random elementary pulsons K_{p,r,i,m,r,i,m} (213)-(214) that describe scalar self-interaction of the velocity potential s_r,i,m of the selfsame mth elementary oscillon (209)-(210) from the selfsame ith random wave group for i = 1, 2, ..., I and m = 1, 2, ..., M.

The random internal wave oscillons (197), (220) consist of two of I(I − 1)/2 random internal elementary oscillons K_{o,r,i,m,r,j,m} (218)-(219) that represent scalar internal interaction of the velocity potentials s_r,i,m and s_r,j,m of the mth elementary oscillons from the distinct ith and jth random wave groups for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, and m = 1, 2, ..., M.

The random diagonal wave oscillons (188), (225) are constructed of three of I random diagonal elementary oscillons K_{o,r,i,m,r,i,n} (223)-(224) that express scalar external interaction of the velocity potentials s_r,i,m and s_r,i,n of the distinct mth and nth elementary oscillons from the selfsame ith random wave group for i = 1, 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

The random external wave oscillons (201), (230) include two of I(I − 1)/2 random external elementary oscillons K_{o,r,i,m,r,j,n} (228)-(229) that expose scalar external interaction of the velocity potentials s_r,i,m, s_r,j,n and s_r,j,m, s_r,i,n of the distinct mth and nth elementary oscillons from the distinct ith and jth random wave groups for i = 1, 2, ..., I − 1, j = i + 1, i + 2, ..., I, m = 1, 2, ..., M − 1, and n = m + 1, m + 2, ..., M.

The vector non-diagonal external interaction for j ≠ i and n ≠ m is described by a superposition of dot products s_r,i,m·s_r,j,n + s_r,j,m·s_r,i,n (200). Consequently, the vector non-diagonal internal interaction for j ≠ i and n = m is expressed by a single dot product s_r,i,m·s_r,j,m (196) and the vector diagonal external interaction for j = i and n ≠ m is represented by a single dot product s_r,i,m·s_r,i,n (187), as well. Ultimately, the vector diagonal internal interaction for j = i and n = m also is reduced to a single dot product s_r,i,m·s_r,i,m (183).

Topology of the random cumulative pulson, the random energy pulson, the random group pulsons, the random wave pulsons, and the random elementary pulsons is the same as topology of the solitons on shallow water, the solitary waves on shallow water with uniform and linear vorticity [10] [11] , the solitary waves generated by crossed electric and magnetic fields [12] , and the pulsatory waves of the Korteweg-de Vries equation [13] .

Topology of the random internal energy oscillon, the random diagonal energy oscillon, the random external energy oscillon, the random internal group oscillons, the random diagonal group oscillons, the random external group oscillons, the random internal wave oscillons, the random diagonal wave oscillons, the random external wave oscillons, the random internal elementary oscillons, the random diagonal elementary oscillons, and the random external elementary oscillons resembles topology of the nonlinear waves and solitons on deep water [14] .

To continue the classical Reynolds approach to fluid-dynamic turbulence it is necessary to describe interaction between the deterministic chaos of exponential oscillons and pulsons [1] and the stochastic chaos of random exponential oscillons and pulsons developed in the current paper. Another open problem is construction of smooth random functions of time, which will give an opportunity to visualize and analyze quantization of the stochastic chaos, as it was done for the deterministic chaos in [3] [4] for the Fourier and Bernoulli sets of wave parameters, respectively.

Acknowledgements

The support of CAAM and the College of Mount Saint Vincent is gratefully acknowledged. The author would like to thank a reviewer for valuable comments, which have improved the paper.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Miroshnikov, V.A. (2020) Deterministic Chaos of Exponential Oscillons and Pulsons. American Journal of Computational Mathematics, 10, 43-72. http://dx.doi.org/10.4236/ajcm.2020.101004
[2]	Miroshnikov, V.A. (2017) Harmonic Wave Systems: Partial Differential Equations of the Helmholtz Decomposition. Scientific Research Publishing, USA. http://www.scirp.org/book/DetailedInforOfABook.aspx?bookID=2494
[3]	Miroshnikov, V.A. (2023) Quantization of the Kinetic Energy of Deterministic Chaos. American Journal of Computational Mathematics, 13, 1-81. https://doi.org/10.4236/ajcm.2023.131001
[4]	Miroshnikov, V.A. (2023) Quantization and Turbulization of Deterministic Chaos of the Exponential Oscillons and Pulsons. BP International, India, United Kingdom. https://stm.bookpi.org/QTDCEOP/issue/view/1045 https://doi.org/10.9734/bpi/mono/978-81-19217-39-7
[5]	Miroshnikov, V.A. (2014) Conservative Interaction of N Internal Waves in Three Dimensions. American Journal of Computational Mathematics, 4, 329-356. http://dx.doi.org/10.4236/ajcm.2014.44029
[6]	Miroshnikov, V.A. (2014) Conservative Interaction of N Stochastic Waves in Two Dimensions. American Journal of Computational Mathematics, 4, 289-303. http://dx.doi.org/10.4236/ajcm.2014.44025
[7]	Korn, G.A. and Korn, T.M. (2000) Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. Revised Edition, Dover Publications, New York.
[8]	Pozrikidis, C. (2011) Introduction to Theoretical and Computational Fluid Dynamics. 2nd Edition, Oxford University Press, Oxford.
[9]	Kochin, N.E., Kibel, I.A. and Roze, N.V. (1965) Theoretical Hydromechanics. Interscience Publishers, New York.
[10]	Miroshnikov, V.A. (2002) The Boussinesq-Rayleigh Approximation for Rotational Solitary Waves on Shallow Water with Uniform Vorticity. Journal of Fluid Mechanics, 456, 1-32. http://dx.doi.org/10.1017/S0022112001007352
[11]	Miroshnikov, V.A. (1996) The Finite-Amplitude Solitary Wave on a Stream with Linear Vorticity. European Journal of Mechanics, B/Fluids, 15, 395-411.
[12]	Miroshnikov, V.A. (1995) Solitary Wave on the Surface of a Shear Stream in Crossed Electric and Magnetic Fields: the Formation of a Single Vortex. Magnetohydrodynamics, 31, 149-165. http://mhd.sal.lv/contents/1995/2/MG.31.2.5.R.html
[13]	Miroshnikov, V.A. (2014) Interaction of Two Pulsatory Waves of the Korteweg-de Vries Equation in a Zigzag Hyperbolic Structure. American Journal of Computational Mathematics, 4, 254-270. http://dx.doi.org/10.4236/ajcm.2014.43022
[14]	Infeld, E. and Rowlands, G. (2000) Nonlinear Waves, Solitons and Chaos. 2nd Edition, Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9781139171281