Elements of Time

Viktor Ariel

Independent Researcher, Modiin, Israel.

DOI: 10.4236/jmp.2023.1411089                

Abstract

A clear mathematical theory of time remains one of the most difficult challenges of science, which seems highly intriguing. In this work, we assume that time is the main independent attribute of nature and therefore may serve as the foundation of a comprehensive field theory. Furthermore, we assume that division algebras with the Euclidean norm are essential mathematical tools of time and the physical world in general. We use a four-dimensional normed division algebra of quaternions to describe time mathematically, as originally envisioned by Hamilton. We systematically define basic quaternion concepts related to time, such as the quaternion time interval, scalar measured time, the arrow of time, vector velocity, and quaternion frequency. We apply quaternion time concepts to the optical Doppler effect and demonstrate that our approach predicts known experimental results. Furthermore, we show that the quaternion solution of the Doppler effect enhances the relativity theory by resolving the notorious twin paradox. We identify quaternion frequency with the traditional concept of energy. We assume that quaternion energy, which is generally dependent on time and external interactions, can be used to describe dynamic properties of matter. In conclusion, we suggest that a state of matter can be represented by the eight-dimensional octonion configuration space, consisting of a quaternion time interval and a time dependent quaternion frequency. Therefore, it appears that the application of normed division algebras for the study of time and nature is highly logical, credible, and compelling.

Keywords

Algebra of Time, Space-Time Physics, Doppler Effect, Relativity Theory

1. Introduction

Recently, there has been significant interest in the physical, mathematical, and philosophical nature of time [1] [2] [3] [4] , and [5] . However, a comprehensive mathematical theory of time seems elusive, even though the concepts of time and motion were investigated in the early days of science. For example, initial ideas on time and motion appear in Euclid’s famous book on Optics [6] .

Newton [7] formally defined space and time as separate entities, including the concepts of absolute and relative time, and applied them to the study of gravitation. Clearly, gravitational force between celestial bodies is acting from a great distance; therefore, Newton introduced the concept of action at a distance, which he assumed to be instantaneous.

Maxwell considered light as an electromagnetic wave traveling with the maximum speed, c, of any interaction. Consequently, this introduced a finite delay for any action at a distance due to the maximum speed of propagation.

For example, consider a transmitter of an electromagnetic wave located a vector distance, , from the origin of the coordinate system, where we place the receiver of the interaction, as in Figure 1. Intuitively, we expect that the signal emitted by the transmitter will arrive at the receiver with a time delay caused by the finite speed of signal propagation, which we may express as,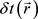. Note that the time delay appears as a function of the three-dimensional vector space.

Doppler [8] suggested a key breakthrough in the study of time and motion during his observations of optical frequency shift of binary stars. Crucially, the Doppler effect shows that a measured frequency shift depends on a relative velocity between the transmitter and receiver as well as on the direction of their relative motion.

Let us now depict the main result of the Doppler effect, namely the dependence of the Doppler frequency shift, 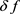, on both the speed and direction of relative motion, , as shown in Figure 2. Let us assume that the stationary receiver is located at the origin while a remote transmitter moves with a constant three-dimensional vector velocity,.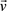

Figure 1. Time delay of an electromagnetic signal propagation from a distant transmitter to a receiver at the origin, as a function of the three-dimensional distance,.

Figure 2. The Doppler frequency shift due to relative motion between a moving transmitter and a stationary receiver as a function of the relative velocity,.

Therefore, we need to account for two experimental effects related to time measurement at a distance. First, we need to describe a time delay of any interaction as a function of the three-dimensional vector distance. Second, we need to account for the frequency shift of electromagnetic waves, due to the relative motion between the transmitter and receiver, as a function of the three-dimensional vector velocity,

(1)

The first comprehensive mathematical treatment of the optical Doppler effect was proposed by Woldemar Voigt [9] [10] , who used a four-dimensional transformation of time and space coordinates to derive it. This major development was later re-introduced and further developed by Lorentz [11] [12] , who was apparently a close acquaintance of Voigt [10] . Later, the spacetime transformation became known as the Lorentz coordinate transformation [13] . We can define the measured time at a stationery receiver, which is located at the origin as, 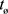, while time at a remote transmitter was defined by Lorentz [11] [12] as the location dependent local time:

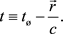(2)

Conceptually, t, is the time of the electromagnetic signal emission by the remote transmitter and, 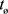, is the time of the signal detection by the stationary receiver. As presented by Voigt and Lorentz, the signal transmitter is located at a real vector location, , away from the receiver. Note that the negative sign in (2) implies that emission of light by the remote transmitter occurred before the signal detection by the stationary receiver.

Using (2), one can possibly introduce the remote time interval,

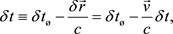(3)

assuming constant velocity of propagation,.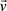

Then, somehow a pseudo-Euclidean quadratic norm of (3) was introduced,

(4)

leading to the time interval transformation known as the Lorentz time dilation,

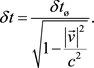(5)

Curiously, the four-dimensional real-valued representation of the local time (2) created some notable mathematical challenges. First of all, any measurement of time with a clock typically results in a one-dimensional real scalar quantity, , as correctly appears on the left-hand-side of (2). This is clearly inconsistent with the four-dimensional real time value on the right-hand-side of (2), where,.

In addition, it seems mathematically impossible to justify the quadratic norm (4) of the time interval (3) as there seems to be no consistent mathematical procedure for calculating the norm of a four-dimensional real quantity.

In order to resolve the issue of the quadratic norm (4), Poincare [13] , who was a friend of Lorentz, proposed an ad hoc but revolutionary and long-reaching mathematical solution. Poincare inserted an imaginary unity element, , in front of the time variable, leading to an imaginary time value and non-Euclidean, curved spacetime,

(6)

At first glance, this ingenious mathematical trick allowed derivation of a quasi-Euclidean quadratic norm (4) by squaring elements of (6). However, this approach did not resolve the mathematical conflict between the one-dimensional measured scalar time and the four-dimensional local time in (2). Despite these mathematical reservations, Einstein [14] [15] and his professor Minkowski [16] , used a similar four-dimensional spacetime (6) and the resulting Lorentz time dilation (5) in the theory of relativity. The spacetime (6) became the Minkowski spacetime, and eventually transformed into the mathematical foundation of the modern science.

Given the above mathematical uncertainty associated with the four-dimensional local time (2), it seems reasonable to consider some alternative approaches to (6).

Another mathematical concept of the four-dimensional time was proposed by Hamilton [17] , who also used algebraic methods of complex numbers in his investigation of an “algebra as the science of pure time”. This led to his development of the Euclidean four-dimensional normed division algebra of quaternions [18] . It seems that Hamilton always expressed a firm belief [19] that a quaternion time element is composed of a one-dimensional real scalar time, , and three-dimensional imaginary space, ,

(7)

This quaternion approach is fundamentally different from the Poincare-Minkowski approach, where time is a one-dimensional imaginary component, , and space is a three-dimensional real vector, of the four-dimensional spacetime (6).

Previously, a mixed vector quaternion representation of time was proposed by Machicote [20] . An extensive study of the relativistic and quantum time concepts using Minkowski approach was performed by Horwitz et al. [21] [22] [23] , and [24] .

Amazingly, Felix Klein, who established the world famous center for mathematics research at the University of Gottingen, where he was a colleague of both Voigt and Minkowski, considered the possibility of “...brilliant applicability of quaternions to the theory of relativity.” [25] .

In this work, we will attempt to demonstrate that the Hamilton’s quaternion formulation of four-dimensional time results in a simple, logical, and compelling mathematical theory of time. Furthermore using quaternion time, we will derive the correct formulation of the optical Doppler effect as experimentally demonstrated by Ives and Stilwell [26] [27] . Additional examples of quaternion dynamics and quaternion Maxwell equations can be found in [28] [29] , and [30] .

2. Postulates of Time Algebra

We begin our study with basic definitions and postulates of time using the mathematical framework of normed division algebras.

Postulate 1 (Time - Main Attribute). We assume that time is the main independent attribute of nature, where the time continuum is infinite, uniform, and absolute.

Normed division algebras have the following useful properties: every non-zero element has a multiplicative inverse and a positive Euclidean norm. Consequently, all usual mathematical operations of addition, subtraction, multiplication, and division are applicable and reversible. The most astonishing property of normed division algebras is that only four such algebras exist. It has been demonstrated By Frobenius [31] and Hurwitz [32] that normed division algebras exist only with dimensions of one, two, four, and eight.

Theorem 1 (Frobenius Division Algebras). All normed division algebras are isomorphic only with the real numbers, , the complex numbers, , the quaternions, , and the octonions,.

Importantly, elements of normed division algebras can be expressed in trigonometric form using the complex exponential Euler relation. Therefore, application of normed division algebras as mathematical tools of nature seems highly compelling.

Postulate 2 (Normed Division Algebras). Normed division algebras constitute essential mathematical tools of time specifically and nature in general.

Let us introduce a concept of four-dimensional, quaternion time moment as a natural mathematical representation of time, as originally suggested by Hamilton.

Postulate 3 (Quaternion Time Moment). The quaternion time moment is an infinitesimal point within the quaternion time continuum, composed of a one-dimensional real scalar time, , and a three-dimensional imaginary vector time, ,

(8)

Here, , is similar to a traditional scalar time measured with a clock, while, , is responsible for the time delay and frequency shift due to action at a distance. Clearly, when time delay and Doppler frequency shift are not important, we can express time as a simple real scalar value.

Please note that in this work we represent quaternions using boldface characters, real scalars as regular italic mathematical symbols, while imaginary vectors with an arrow above the character, similar to traditional real three-dimensional vectors.

To express quaternion time numerically, we introduce a quaternion time coordinate system. A coordinate representation is relative, depending on the choice of coordinate axes and the origin of the coordinate system. For example using an orthogonal Cartesian coordinate system leads to the following Cartesian representation of a quaternion time moment,

(9)

Here, , are real numbers. The mathematical relations between the quaternion unit elements, , and, , are essential for the present theory and were defined using quaternion multiplication by Hamilton [18] . We depict a simplified three-dimensional quaternion time coordinate point in Figure 3, where we neglect the z-axis for simplicity.

Figure 3. A three-dimensional representation of a quaternion time coordinate point.

The coordinate quaternion time representation also depends on a choice of the origin of the quaternion time coordinate system,

(10)

In order to identify physical time at a distance, we use the concept of location dependent quaternion time or the local time, similar to the four-dimensional local time concept introduced by Voigt and Lorentz.

Postulate 4 (Quaternion Local Time). Given the quaterion coordinate system and its origin, a quaternion local time point, , uniquely represents time information at a distant three-dimensional space location, , away from the origin,

(11)

Note that this definition of, , resembles the time flow parameter of the Stueckelberg-Horwitz-Piron (SHP) formalism in relativity [22] [23] [24] , however, represented in the quaternion form unlike the Minkowski form in SHP.

Postulate 5 (Maximum Speed). There exists a maximum speed of signal propagation, which we identify with the speed of light, c, and which acts as a coefficient of proportionality between space and time. As we will demonstrate later in this work, the existence of the maximum speed follows from the mathematical definition of velocity and quaternion properties of time. Thus, the speed of light, c, represents the first natural constant of the present theory.

A three-dimensional space point in the imaginary vector space can be represented using Cartesian time coordinates,

(12)

Also, we can express a quaternion time coordinate point using the following convenient form, similar to a two-dimensional complex number,

(13)

where we define a unity three-dimensional imaginary vector,

(14)

where,. Here, the one-dimensional imaginary axis is chosen along the three-dimensional unity space vector, , which allows a simpler two-dimensional representation of the four-dimensional quaternion time points. This choice of coordinates allows us to represent a quaternion time moment similar to a two-dimensional Agrand’s diagram of complex numbers, as shown in Figure 4.

Note that for convenience, we chose a real scalar time vertical axis and an imaginary three-dimensional space horizontal axis, unlike the typical choice of imaginary vertical axis in a complex number representation.

Let us introduce a source quaternion time point as. Similarly, we define a destination quaternion time point as.

Figure 4. A quaternion time coordinate point using two-dimensional representation, where three-dimensional space is reduced to a single coordinate axis.

Postulate 6 (Quaternion Time Interval). The quaternion time interval is a four-dimensional arrow signifying a transition in the quaternion time continuum from the source time point to the destination time point. Thus, a quaternion time interval, , is the difference between the destination quaternion time point, , and the source quaternion time point,.

(15)

where, , is the scalar time interval and, , is the vector time interval.

The definition of a quaternion time interval is depicted in Figure 5. Note that the direction of the quaternion time interval is always from the source point to the destination point. Since a quaternion time interval is an algebraic difference between two quaternion values, it can be represented as a single quaternion coordinate point. We achieve this by moving the origin of the quaternion time coordinate system either to the source point or to the destination point.

Therefore, for each quaternion time interval, there are two different representations as a single quaternion time coordinate point. One possible representation shows transition from the origin to the destination point, , while the other represents a transition from the negative source point, , to the origin, as shown in Figure 6.

(16)

This distinction of motion towards or away from the origin is crucial for the description of the Doppler shift experiment using quaternion time.

Figure 5. A quaternion time interval in three dimensions.

Figure 6. Two representations of a quaternion time interval, including the source at the origin and the destination at the origin.

Postulate 7 (Past, Present, and Future). We can identify the origin of the quaternion time coordinate system with the present time. Therefore, all time intervals terminating at the origin started in the past and all time intervals starting at the origin have destinations in the future.

Alternatively, we can consider the definition of quaternion time interval as a transformation of the quaternion time coordinate system, where the zero-point transitions from the source point to the destination point by a quaternion time interval,. Even for stationary objects in three-dimensional space, the quaternion time, , is constantly progressing due to the relentless progression of scalar time,. Consequently, the progression of quaternion time is due to the transition of the zero-point between past, present, and future embedded in the definition of the quaternion time interval.

Because of the spatial symmetry of the three-dimensional space under reflection, we can repeat the experiment, reversing all the space directions. The conjugate quaternion quaternion time interval is defined as,

(17)

Consequently, all quaternion time intervals and points switch their vector time directions, which results in the conjugate quaternion time representation, shown in Figure 7.

Postulate 8 (Quaternion Time Symmetry). 1) The scalar quaternion time interval, , is continuously, uniformly, and relentlessly progressing from the past into the future, consequently, it is not symmetric under scalar axis reflection. 2) The three-dimensional vector time, , is stationary, uniform, and symmetric under operations of translation and rotation.

Thus, we defined a basic four-dimensional quaternion time event, , which represents quaternion time at a destination-point located distance, , away from the origin. The minimum vector time delay is represented by, , which accounts for action at a distance.

Therefore, the four-dimensional quaternion time appears as promising approach for specifying time at a distance. However, we need to establish a correspondence between the four-dimensional quaternion time moment and the real scalar measured time moment, which we see on a clock.

Postulate 9 (Absolute Value of Time). Using properties of quaternion division, which are similar to complex numbers, we define the multiplicative inverse of the quaternion time interval,

Figure 7. A mirror reversal of the space direction results in the conjugate quaternion representation of the quaternion time intervals.

(18)

where, , is the absolute value of the time interval equal to the Euclidean norm of the interval.

Using definitions of the quaternion time interval (15) and its conjugate (17) and applying the definition of the multiplicative inverse (18),

(19)

Note that we thus proved a quaternion version of the Pythagorean theorem using the algebraic definition of quaternion multiplicative inverse.

Postulate 10 (Measured Time). The everyday scalar time interval measured with a clock is equal to the absolute value of the quaternion time interval, which we always measure in the past.

This is the key postulate of the present work allowing a link between the quaternion algebra of time and everyday experimental measurements of time performed with a clock. Note that we can perform time measurement only in the past, which is the key difference between past and future.

Let us define a scalar measured time moment, tau, as the infinitesimal instance of time that can be measured with a clock.

We can calculate measured time, , at the quaternion time destination point, , as a sum of the measured time, , at the source point, , and the corresponding absolute time interval,

(20)

where the absolute time moment at the zero-point source is equal to zero.

It appears that mathematically the process of time interval measurement is equivalent to a rotation of the quaternion time interval in the direction of the scalar invariant time axis,. A comparison between a quaternion time interval, , absolute time interval, , and measured time interval is shown in Figure 8.

Note that first we bring the quaternion time interval, , whose absolute value, , we would like to measure into the stationary coordinate system of the detector. To achieve this, we move the current-time to the source-point and rotate the quaternion time interval to the scalar axis. Thus, the absolute time interval becomes equal to the scalar time interval,. Next, we perform an experimental measurement of the absolute time interval with a clock, which transfers the measured time interval into the past.

Thus, we succeeded in making a mathematical connection between quaternion time and scalar measured time. The relation is obtained from the quaternion Euclidean absolute value of the quaternion time interval.

The quaternion time path, is a sequence of connected quaternion time intervals from the source point and ending at the final destination point.

The total quaternion time interval is a sum of individual quaternion time intervals, , along the quaternion time path,

Figure 8. Measurement procedure of a quaternion time interval corresponding to a rotation of the quaternion time interval towards the scalar axis.

(21)

Thus, the total quaternion time interval is equal to the interval from the source point to the final destination point. We assume that the path of time can be broken into, N, discrete quaternion time intervals. Also in this model, we assume that all changes in the quaternion time intervals are due to interactions that happen instantaneously at the quaternion time points, while quaternion time intervals represent inertial motion of carriers between the quaternion time points of interaction.

The measured length of the quaternion time path, , is equal to the sum of the individual measured quaternion time intervals, , along the time path from the source-point to the destination-point.

(22)

However, multiple different time paths leading to the same quaternion time point, , will result in different measured times. Multiple time paths and simultaneous events are shown in Figure 9.

Therefore, quaternion time moments may have different measured time intervals depending on their respective time paths.

Postulate 11 (Arrow of Time). Using properties of quaternions, we can always express a quaternion time interval as its absolute value multiplied by a unity quaternion, which we call the arrow of time,.

(23)

where,

(24)

Figure 9. Multiple paths arriving at the same quaternion time point may result in different measured times depending on the time path.

Consequently, the quaternion time interval is equal to the measured scalar time interval multiplied by the quaternion arrow of time. The arrow of time can be expressed using the definition of the quaternion time interval (15) as,

(25)

The arrow of time and the quaternion time interval are shown in two-dimensional representation in Figure 10.

By our convention, action at a distance has a positive direction from the start to the destination, therefore, we choose the positive direction of the arrow of time as the direction of transition from the source point, , to the destination point,.

Thus, the quaternion time interval, , corresponds to a transition of carriers from the start to the destination. We define a vector velocity, , of a carrier making a transition in space, , during the scalar time interval, ,

(26)

where we define radial velocity, , and rotational velocity,. Also, note that we can define angular velocity,.

As usual, we can introduce the unity velocity as a purely imaginary unity three-dimensional vector,

(27)

which determines the direction of the velocity vector, , and consequently represents the direction of motion in three-dimensional space generally consisting of radial and rotational motion.

Figure 10. A quaternion time interval and its arrow of time.

Note that while defining the vector velocity, we relied on the four-dimensional nature of quaternion time by using the quaternion norm for the time interval,.

Using the definition of the vector velocity, we can write the arrow of time as,

(28)

Note that motion in the opposite direction is given by the conjugate arrow of time,

(29)

The arrow of time and its conjugate define an infinite straight line in the four-dimensional quaternion time continuum.

The length of the arrow of time is unity, consequently,

(30)

Thus, we obtained a relation between the scalar time interval, , of a stationary source and the scalar length of the remote time interval, , during motion,

(31)

which is similar to the Lorentz time dilation.

Note that mathematically the result is a simple consequence of the quaternion Euclidean metric of the quaternion time as expressed by the length of time,.

Using (30) and (31), we can express the arrow of time in terms of velocity only,

(32)

Thus, the arrow of time represents a direction and trajectory of motion with velocity, , generally representing radial and rotational motion.

One of the key useful properties of quaternion algebra is the availability of Euler’s formula, which we use to express the arrow of time as,

(33)

where we define the angle between the quaternion time interval and the scalar time axis, , as the phase of time or Aeon, which is determined by the velocity using,

(34)

As anticipated, this leads to,

(35)

Thus, the maximum speed of any inertial motion is equal to, c, which is a consequence of mathematical properties of quaternion time and the definition of the vector velocity.

We can now express the quaternion time interval as a function of its absolute value and vector velocity,

(36)

Therefore, the absolute value of the time interval, , determines the measured time interval, while the arrow of time determines all the dynamic properties including the speed and direction of motion. The quaternion time interval provides a complete description of time, space, and motion during inertial transition from the source quaternion time point to the destination quaternion time point,

(37)

In Figure 11, is a three-dimensional representation of a quaternion time interval, , together with the phase of time.

Postulate 12 (Arrow of Time and Causality). The arrow of time signifies the direction of the time flow in the four-dimensional quaternion time manifold and consequently determines the direction of causality.

Figure 11. A three-dimensional (z = 0) representation of a quaternion time interval including arrow of time.

Note that the notion of time flow and causality was discussed in [21] and appears in the SHP formalism of relativity [22] [23] [24] .

3. Doppler Effect Using Time Algebra

Let us consider an electromagnetic signal transmitter that produces a periodic electromagnetic wave with a period described by the time interval, , at the origin of the coordinate system, where we place the signal transmitter. As we demonstrated, the electromagnetic wave at the remote location can be described by a periodic signal with a period,. Consider the quaternion time diagram in Figure 12, where we depict a stationary transmitter at the origin and a moving receiver at the remote location.

Then, using the properties of quaternion division we define the quaternion frequency as a multiplicative inverse of the quaternion time interval.

Postulate 13 (Quaternion Frequency). Let us assume that a velocity dependent quaternion frequency at a remote location is a multiplicative inverse of the quaternion time interval,

(38)

Note that the quaternion frequency is proportional to the conjugate of the corresponding quaternion time interval, $\delta \bar{\tau }$ .

Presently, we will consider only the radial relative motion of the transmitter and receiver along their mutual axis, while the circular motion can be similarly obtained from the definition of the quaternion frequency (38).

Postulate 14 (Measured Frequency). Let us assume that the measured frequency at a remote location is the absolute value of the quaternion frequency there,

Figure 12. Quaternion time interval of a stationary transmitter and a receiver moving away from the transmitter.

(39)

where, is the measured frequency at the origin.

Let us consider physical interpretation of the Doppler effect using definitions of the quaternion time interval and quaternion frequency. First, we consider radial motion of a receiver moving away from a stationary transmitter, as in Figure 12. Here, the light signal is represented by the horizontal wavy line from the origin to the final location of the receiver. The motion of the receiver is represented by a solid line from the source at the origin to the final destination point. We can determine the relationship between time intervals at the transmitter and the receiver.

(40)

This leads to the traditional time dilation equation for the time intervals,

(41)

We assume that all observed time intervals transform according to (41) and thus we can apply the time interval dilation to the calculation of the light wave frequency at a remote location. Therefore, the measured light wave frequency ratio at the receiver, , and the transmitter, , is calculated as,

(42)

Next, let us consider a stationary receiver located at the origin and a transmitter of the light signal approaching the receiver, as in Figure 13. Again, we represent the light signal as a horizontal line from the transmitter to the receiver. This allows us to calculate the observed time interval dilation, which results in identical time dilation to the previous case (41). However, the relative locations of the transmitter and receiver are switched and we obtain an inverse relation for the Doppler frequency shift, using Figure 13,

(43)

These results are clearly in agreement with everyday experience of the Doppler effect and correspond to experimental measurements of the optical Doppler shift as demonstrated by Ives and Stilwell [26] [27] . Note that the traditional relativistic Doppler results [14] and [15] are only similar to the proper quaternion Doppler expressions (42) and (43) in the case of the transverse Doppler effect. The present quaternion Doppler frequency transformation is derived from the general quaternion frequency expression (38), which is valid for any arbitrary motion.

4. Application of Time Algebra to Relativity

We demonstrated that the remote time interval can be represented by a quaternion time interval expression, while the measured time interval is given by the absolute value. Also, we interpreted a quaternion time interval as a physical transition between the source and destination with vector velocity,.

Figure 13. Quaternion time interval of a moving transmitter approaching a stationary receiver.

Using the definitions of the time interval (15) and the quaternion frequency (38), we can express quaternion time and frequency at the destination point,

(44)

Here we define the frequency interval between the destination and start points as,.

Therefore, the quaternion algebra of time delivers transformations at a distance of both the time interval and the frequency. Alternatively, we can view the time and frequency transformation (44) as the coordinate system transition from the start point to the destination point.

Postulate 15 (Relativistic Coordinate Transformation). The quaternion time interval and frequency transformations (44) represent an eight-dimensional relativistic coordinate system transformation, which is due to the measurement at a distance and the corresponding Doppler effect.

Let us suggest a thought experiment of the optical Doppler effect that leads to a novel interpretation of the twin experiment of the special theory of relativity. Let us consider a transmitter of a periodic signal, such as a clock on a kitchen wall, which is also the origin of our stationary coordinate system. Let us also assume the existence of a signal receiver, such as a cook, located close to the kitchen clock and capable of observing the time interval and the corresponding period of clock oscillations. Then, assuming a constant distance between the cook and the stationary kitchen clock, the observed time interval by the cook is equal to, , which is the same time interval appearing on the kitchen clock.

Next, let us assume that the cook has a twin who is launched into space on a spaceship equipped with a spaceship clock. Assume that all the clocks are synchronized prior to the spaceship launch and that the spaceship travels in a straight line away from the cook. After the launch, the twin on the moving spaceship observes the stationary clock on the kitchen wall using a telescope. The twin can see the remote time interval, on the kitchen wall, while observing time interval, , on the spaceship clock, as shown in Figure 12.

Since the kitchen clock is moving away from the spaceship, the time interval and the period of clock oscillations observed by the twin on the spaceship clock will appear longer relative to the stationary kitchen clock. This apparent remote time interval increase appears as a result of the remote measurement procedure and the optical Doppler effect, as shown in Figure 12 and expressed by (42).

Next, let us assume that the spaceship turns around and starts moving in the direction of the kitchen clock. This time, the stationary cook is watching the clock on the moving spaceship with a telescope while comparing the measurement to the stationary kitchen clock. The time interval of the stationary kitchen clock will appear relatively shorter than the interval of the moving spaceship clock, observed with the telescope by the cook. This is entirely due to the Doppler period decrease at the stationary receiver relative to the approaching transmitter, as shown on Figure 13 and expressed by (43).

Consequently, the time interval change during the round trip will cancel out due to the bi-directional nature of the Doppler effect. This implies that upon reunification, the cook and the twin will be exactly the same age and all the clocks will show exactly the same time.

In conclusion, the clock period shift observed during motion of the transmitter relative to the receiver is entirely due to the Doppler effect and the remote measurement at a distance.

Postulate 16 (Relative Time and Frequency due to Doppler Effect). Measured time intervals and clock periods do not change if the relative distance between the transmitter and receiver remains constant. However, remotely measured time intervals and clock periods change depending on the speed and direction of relative motion due to the Doppler effect.

Therefore, the relative change in the time interval and the frequency at the receiver location relative to the transmitter is entirely due to the remote time measurement and Doppler effect, which can be calculated using the division algebra of quaternions.

5. Quaternion Matter and Dynamic Properties

So far, we only considered the frequency shift of a monochromatic wave, which allowed us to calculate the Doppler frequency shift, using the definition of the quaternion frequency interval,

(45)

Postulate 17 (Quaternion Energy). Let us assume that the quaternion frequency function describes the energy of a monochromatic light wave,

(46)

Here, h, is the Planck constant, which relates the energy to the frequency and becomes the second most important parameter of the present theory in addition to the speed of light, c. Also, , is the scalar potential energy, while, is the vector energy due to motion, which defines the kinetic energy.

Generally, we expect a signal to be composed of a number of harmonics, corresponding to a range of quaternion frequencies with the resulting quaternion wave packet,

(47)

We assume here that the energy of the wave packet can be described similar to the energy of a monochromatic wave (46).

Postulate 18 (Quaternion Mass). Next, we use (46) and introduce the quaternion mass of the wave using Einstein’s energy-mass relation in quaternion form,

(48)

where we define the vector momentum as,

(49)

Thus far, we obtained the quaternion description of inertial particle motion given by the inertial energy,

(50)

Next, let us consider what happens when external interaction is present. We need to distinguish between the externally applied energy, which does not depend on the particle and material properties, and the energy of a particle under the influence of the external energy. For example, an electron immersed inside a material such as a semiconductor.

Postulate 19 (Quaternion External Interaction). Let us assume that the external interaction can be expressed by an external quaternion energy similar to the free particle energy,

(51)

For example, in the case of an external electromagnetic interaction we express the external energy using a quaternion electromagnetic potential,

(52)

where, q, is the particle charge, which represents electromagnetic interactions, and becomes another important parameter of the theory.

Then, we express the total quaternion particle energy, including the free particle motion together with external electromagnetic interaction,

(53)

Using the definition of the Euclidean norm, we can easily obtain the square of the absolute value of the total energy,

(54)

which is similar to the relativistic Dirac and Klein-Gordon equations and thus describes the dynamic properties of charged particles in the presence of an external electromagnetic interaction.

Postulate 20 (Measured Total Energy). Let us assume that the measured energy is equal to the Euclidean norm of the quaternion energy,

(55)

In the presence of external electromagnetic interaction, the total energy is generally not a constant function of time. Therefore, we assume that total quaternion energy is generally time dependent, such that,

(56)

Note that in this interpretation, the quaternion time, , plays the role of the system evolution parameter, similar to time interpretation in the SHP formalism [22] [23] [24] , while the scalar measured time, , is the absolute value of the quaternion time.

Finally, we introduce quaternion coordinate transformations in the presence of external interactions using (44),

(57)

Here, the quaternion time interval is the independent variable while the quaternion frequency represents the energy in the presence of an external interaction and consequently, is a function of the quaternion time. Thus, we obtained transformations of the time interval and the frequency in the presence of an external interaction.

The measured values of time and frequency are given by the Euclidean norm of the quaternion time and the quaternion frequency, respectively, thus resulting in a complete model of time and matter dynamics.

Note that we can define the matter density function by dividing the time dependent quaternion frequency, energy, and mass by their absolute values,

(58)

Postulate 21 (Matter Density Function). Using the quaternion Euler relation, we realize that the matter density function is generally a periodic function of,

(59)

Also, we note that

(60)

Note that the quaternion matter density function appears similar to the wave function of quantum mechanics.

Finally, similar to the SHP formalism [23] , we can introduce an eight-dimensional octonion time configuration space, , where the quaternion time, , is the main independent attribute and the quaternion frequency, , which is generally time dependent and is the main dynamic attribute describing energy and dynamics.

Postulate 22 (Octonion Configuration Space). All dynamic properties can be obtained using the eight-dimensional octonion configuration space, consisting of the independent quaternion time and the time dependent quaternion frequency,

(61)

Therefore using division algebras, we obtained a highly comprehensive, simple, and compelling mathematical framework of time and matter. Additional examples of quaternion dynamics and quaternion Maxwell equations can be found in [28] [29] , and [30] , which we will explore further in a future work.

6. Conclusion

In conclusion, we used the concepts of four-dimensional local time and a normed division algebra of quaternions to define a comprehensive set of postulates for time algebra. We defined the basic quaternion time concepts, such as the quaternion time interval, the measured time, the path of time, and the arrow of time. We used the Euclidean norm of the quaternion time interval as a connecting link between the quaternion time and the real scalar measured time. Also, we introduced the concepts of quaternion frequency and the measured frequency at a distance. This allowed us to develop expressions for the optical Doppler shift that can be verified by experimental measurements. We used the Doppler effect to explain the twin paradox of the relativity theory thus enhancing the interpretation of relativistic Doppler effect. Using quaternion frequency, we introduced quaternion energy and mass. We assumed that external interactions can be also represented as a quaternion quantity. This allowed us to represent matter dynamics with the help of quaternion matter density function, which is also known as the wave function in quantum mechanics. Finally, we demonstrated that an eight-dimensional octonion configuration space, consisting of quaternion time and the time dependent quaternion frequency, can be used for a description of dynamic properties of matter. Therefore, it appears that by using normed division algebras, we were able to construct a simple, logical, and compelling theory of time and matter.

Acknowledgements

My sincere gratitude to Prof. Shlomo Ruschin of Tel Aviv University for inspiring this work. Many thanks to Gennady Fiksman and Heidi Brun for a comprehensive review of the work. Also, I would like to thank the following contributors for their helpful comments: Prof. Leonid Altschul, Prof. Charles L. Schwartz, Prof. Alan V. Oppenheim, Prof. Jeremy Dunning-Davies, Prof. Sergey G. Fedosin, Valery Garber, Viktor E. Matizen, Solomon Khmelnik, Daniel Alayón-Solarz, Muralidhar Kundeti, Peter M. Jack, and Rich Norman.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Galison, P. (2010) Einstein’s Clocks and Poincare’s Maps: Empires of Time. W.W. Norton & Company, New York.
[2]	Penrose, R. (2010) Cycles of Time: An Extraordinary New View of the Universe. The Bodley Head, London.
[3]	Smolin, L. (2013) Time Reborn: From the Crisis in Physics to the Future of the Universe. Mariner Books, Boston.
[4]	Rovelli, C. (2018) The Order of Time. Riverhead Books, New York.
[5]	Carroll, S. (2022) The Biggest Ideas in the Universe Space, Time, and Motion. Dutton, New York.
[6]	Euclid (1943) The Optics of Euclid, Journal of the Optical Society, 35, 357-372.
[7]	Newton, I. (1728) Philosophiae Naturalis Principia Mathematica, Ed. 3, Definitions and Axioms, Scholium.
[8]	Doppler, C. (1843) Proceedings of the Royal Bohemian Society of Sciences, 5, 465-482.
[9]	Ernst, W. and Hsu, J.P. (2001) Chinese Journal of Physics, 39, 211-230.
[10]	Voigt, A. (1887) On the Principle of Doppler, Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingenaus dem Jahre. v 1887.
[11]	Lorentz, H.A. (1895) Attempt of a Theory of Electrical and Optical Phenomena in Moving Bodies/Section III, §33-§35. E. J. Brill, Leiden.
[12]	Lorentz, H.A. (1904) Proceedings of the Royal Netherlands Academy of Arts and Sciences, 6, 809-831.
[13]	Poincare, H. (1905) Comptes Rendus de l’Académie des Sciences, 140, 1504-1508.
[14]	Einstein, A. (1905) Annalen der Physik, 322, 891-921. https://doi.org/10.1002/andp.19053221004
[15]	Einstein, A. (1907) Annalen der Physik, 23, 197-198.
[16]	Minkowski, H. (1909) Raum und Zeit. Jahresberichte der Deutschen Mathematiker-Vereinigung, 75-88.
[17]	Hamilton, W.R. (1837) Transactions of the Royal Irish Academy, 17, 293-422.
[18]	Hamilton, W.R. (1843) Proceedings of the Royal Irish Academy, 2, 424-434.
[19]	Graves, R.P. (1889) Life of Sir William Rowan Hamilton, 3, 633-635.
[20]	Machicote, J.E.R. (2010) Foundations of Physics, 40, 1744-1778. https://doi.org/10.1007/s10701-010-9479-2
[21]	Horwitz, L.P., Arshnsky, R.I. and Elitzur, A.C. (1988) Foundations of Physics, 18, 1159-1193. https://doi.org/10.1007/BF01889430
[22]	Horwitz, L.P. and Piron, C. (1973) Helvetica Physica Acta, 46, 316-326.
[23]	Horwitz, L.P. (2015) Relativistic Quantum Mechanics. Springer, Berlin. https://doi.org/10.1007/978-94-017-7261-7
[24]	Land, M. and Horwitz, L.P. (2020) Relativistic Classical Mechanics and Electrodynamics. Morgan & Claypool Publishers, San Rafael. https://doi.org/10.1007/978-3-031-02079-7
[25]	Klein, F. (1928) Development of Mathematics in the 19th Century (Lie Groups). Mathematics and Science Press, Brookline, 178.
[26]	Ives, H.E. (1937) Journal of the Optical Society of America, 27, 389-388. https://doi.org/10.1364/JOSA.27.000389
[27]	Ives, H.E. and Stilwell, G.R. (1038) Journal of the Optical Society of America, 28, 215-219. https://doi.org/10.1364/JOSA.28.000215
[28]	Jack, P.M. (2003) Physical Space as a Quaternion Structure. arXiv:math-ph/0307038.
[29]	Ariel, V. (2017) Quaternion Time, Mass, and Particle Velocity. arXiv:1706.04837 [physics.gen-ph].
[30]	Ariel, V. (2021) Quaternion Space-Time and Matter. arXiv:2106.06394.
[31]	Frobenius, G. (1878) Journal für die Reine und Angewandte Mathematik, 84, 1-63. https://doi.org/10.1515/crelle-1878-18788403
[32]	Hurwitz, A. (1898) über die Composition der quadratischen Formen von beliebig vielen Variabeln. Goett. Nachr., 309-316.