Relative Ding Projective Modules over Formal Triangular Matrix Rings

Hongyan Fan¹, Xi Tang^2*

¹College of Science, Guilin University of Technology, Guilin, China.
²School of Science, Guilin University of Aerospace Technology, Guilin, China.

DOI: 10.4236/jamp.2023.116105                

Abstract

Let U be a (B, A)-bimodule, A and B be rings, and be a formal triangular matrix ring. In this paper, we characterize the structure of relative Ding projective modules over T under some conditions. Furthermore, using the left global relative Ding projective dimensions of A and B, we estimate the relative Ding projective dimension of a left T-module.

Keywords

Formal Triangular Matrix Ring, Relative Ding Projective Module, Relative Ding Projective Dimension

1. Introduction

Let A and B be rings an U a $\left(B\mathrm{,}A\right)$ -bimodule, $T=\left(\begin{array}{cc}A& 0\\ U& B\end{array}\right)$ is called a formal

triangular matrix ring with usual matrix addition and multiplication. This kind of ring is useful in the representation theory of algebras and ring theory. It is typically used to create examples and counterexamples, which add more examples and concreteness to the theory of rings and modules. Many authors have studied T in several directions. For example, Zhang [1] specifically described the Artin triangular matrix algebra with Gorenstein projective modules. Enochs, Izurdiaga and Torrecillas [2] characterized Gorenstein projective and injective modules over a triangular matrix ring. Mao [3] studied Gorenstein flat modules over T and provided a left global Gorenstein flat dimension estimate of T. Besides, he [4] studied cotorsion pairs and approximation classes over T.

This paper aims at investigating relative Ding projective modules and relative Ding projective dimension over T. Following is the organization of this paper.

In Section 2, we present some terminology as well as preliminary results.

In Section 3, we describe relative Ding projective modules over T. Assume that ${}_A{C}_1$ and ${}_B{C}_2$ are semidualizing. Let $M={\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}$ , $C=p\left(C_1\mathrm{,}{C}_2\right)\in T\text{-Mod}$ and U be Ding C-compatible. Then a left T-module $M={\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}$ is $D_C$ -projective if and only if $M_1$ is $D_{C_1}$ -projective, Coker ${\phi }^M$ is $D_{C_2}$ -projective, and ${\phi }^M\mathrm{<mo>\; :\; </mo>}U{\otimes }_A{M}_1\to M_2$ is injective.

In Section 4, we estimate the $D_C$ -projective dimension of a left T-module and the left global $D_C$ -projective dimension of T. It is proved that, given a left T-module $M={\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}$ , if $C=p\left(C_1\mathrm{,}{C}_2\right)$ , U is Ding C-compatible, ${}_A{C}_1$ and ${}_B{C}_2$ are semidualizing, and $S{D}_{C_2}\text{-}PD\left(B\right)=\sup \left\{D_{C_2}\text{-}p{d}_B\left(U{\otimes }_{A}D\right)|D\in D_{C_1}P\left(A\right)\right\}<\infty$ , then:

$\begin{array}{l}\max \left\{D_{C_1}\text{-}pd\left(M_1\right),\left(D_{C_2}\text{-}pd\left(M_2\right)-S{D}_{C_2}\text{-}PD\left(B\right)\right)\right\}\le D_C\text{-}pd\left(M\right)\\ \le \max \left\{\left(D_{C_1}\text{-}pd\left(M_1\right)\right)+\left(S{D}_{C_2}\text{-}PD\left(B\right)\right)+1,D_{C_2}\text{-}pd\left(M_2\right)\right\}.\end{array}$

Consequently, we prove that,

$\begin{array}{l}\max \left\{D_{C_1}\text{-}PD\left(A\right),D_{C_2}\text{-}PD\left(B\right)\right\}\le D_C\text{-}PD\left(T\right)\\ \le \max \left\{D_{C_1}\text{-}PD\left(A\right)+S{D}_{C_2}\text{-}PD\left(B\right)+1,D_{C_2}\text{-}PD\left(B\right)\right\}.\end{array}$

So we establish a relationship between the relative Ding projective dimension of modules over T and modules over A and B.

All rings for this article are nonzero associative rings with identity, and all modules are unitary. Unless stated explicitly, all modules will serve as unital left R-modules. For a ring R, we write R-Mod (resp. Mod-R) for the category of left (resp. right) R-modules. For a left R-module C, we use Add_R(C) (resp. add_R(C)) to represent the class that contains all left R-modules that are isomorphic to direct summands of (resp. finite) direct sums of copies of C, and we use Prod_R(C) to represent the class that contains all left R-modules that are isomorphic to direct summands of direct products of copies of C. $\mathcal{P}\left(R\right)$ and $\mathcal{F}\left(R\right)$ denote the classes of projective and flat left R-modules respectively. The character module ${\text{Hom}}_{\mathbb{Z}}\left(M\mathrm{,}\mathbb{Q}\mathrm{<mo>\; /\; </mo>}\mathbb{Z}\right)$ of a module M is signed by M⁺.

Next, we will review some concepts and facts about formal triangular matrix rings. By [ [5] , Theorem 1.5], T-Mod corresponds to the category Ω, whose objects are triples $M={\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}$ , where $M_1\in A\text{-Mod}$ , $M_2\in B\text{-Mod}$ and ${\phi }^M\mathrm{<mo>\; :\; </mo>}U{\otimes }_A{M}_1\to M_2$ is a B-morphism and whose morphisms from ${\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}$ to ${\left(\begin{array}{c}{N}_1\\ N_2\end{array}\right)}_{{\phi }^N}$ are pairs $\left(\begin{array}{c}{f}_1\\ f_2\end{array}\right)$ such that $f_1\in {\text{Hom}}_A\left(M_1\mathrm{,}{N}_1\right)$ , $f_2\in {\text{Hom}}_B\left(M_2\mathrm{,}{N}_2\right)$ satisfying that the following diagram

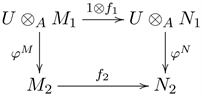
is commutative. Given a triple $M={\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}$ in Ω, there is an A-morphism $\widetilde{{\phi }^M}\mathrm{<mo>\; :\; </mo>}{M}_1\to {\text{Hom}}_B\left(U\mathrm{,}{M}_2\right)$ given by $\widetilde{{\phi }^M}\left(x\right)\left(u\right)={\phi }^M\left(u\otimes x\right)$ for each $u\in U$ , and $x\in M_1$ .

It is worth noting that a sequence $0\to {\left(\begin{array}{c}{M^{\prime }}_1\\ {M^{\prime }}_2\end{array}\right)}_{{\phi }^{M^{\prime }}}\to {\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}\to {\left(\begin{array}{c}{M^{″}}_1\\ {M^{″}}_2\end{array}\right)}_{{\phi }^{M^{″}}}\to 0$ of left T-modules is exact if and only if both the sequences $0\to {M^{\prime }}_1\to M_1\to {M^{″}}_1\to 0$ and $0\to {M^{\prime }}_2\to M_2\to {M^{″}}_2\to 0$ are exact.

Throughout this article, $T=\left(\begin{array}{cc}A& 0\\ U& B\end{array}\right)$ is a formal triangular matrix ring. Given a left T-module $M={\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}$ , the B-module Coker ${\phi }^M$ is denoted as ${\bar{M}}_2$ and the A-module $\ker \widetilde{{\phi }^M}$ is denoted as $\underset{\_}{M_1}$ .

Analogously, Mod-T is equivalent to the category Γ whose objects are triples $W={\left(W_1\mathrm{,}{W}_2\right)}_{{\phi }_W}$ , where $W_1\in \text{Mod-}A$ , $W_2\in \text{Mod-}B$ and ${\phi }_W\mathrm{<mo>\; :\; </mo>}{W}_2{\otimes }_{B}U\to W_1$ is an A-morphism, and whose morphisms from ${\left(W_1\mathrm{,}{W}_2\right)}_{{\phi }_W}$ to ${\left(X_1\mathrm{,}{X}_2\right)}_{{\phi }_X}$ are pairs $\left(g_1\mathrm{,}{g}_2\right)$ such that $g_1\in {\text{Hom}}_A\left(W_1\mathrm{,}{X}_1\right)$ , $g_2\in {\text{Hom}}_B\left(W_2\mathrm{,}{X}_2\right)$ satisfying that the following diagram

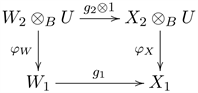
is commutative.

Given such a triple $W={\left(W_1\mathrm{,}{W}_2\right)}_{{\phi }_W}$ in Γ, there is the B-morphism $\widetilde{{\phi }_W}\mathrm{<mo>\; :\; </mo>}{W}_2\to {\text{Hom}}_A\left(U\mathrm{,}{W}_1\right)$ given by $\widetilde{{\phi }_W}\left(y\right)\left(u\right)={\phi }_W\left(y\otimes u\right)$ for each $u\in U$ , and $y\in W_2$ .

In the remaining sections of the paper, we will identify T-Mod (resp. Mod-T) with the category Ω (resp. Γ)

According to [2] , the following functors exist between the category T-Mod and the product category $A\text{-Mod}\times B\text{-Mod}$ :

1) $p\mathrm{<mo>\; :\; </mo>}A\text{-Mod}\times B\text{-Mod}\to T\text{-Mod}$ is defined as follows: for each object ( $M_1\mathrm{,}{M}_2$ ) of $A\text{-Mod}\times B\text{-Mod}$ , let $p\left(M_1\mathrm{,}{M}_2\right)=\left(\begin{array}{c}{M}_1\\ \left(U{\otimes }_A{M}_1\right)\oplus M_2\end{array}\right)$ with the obvious map and for any morphism ( $f_1\mathrm{,}{f}_2$ ) in $A\text{-Mod}\times B\text{-Mod}$ , let $p\left(f_1\mathrm{,}{f}_2\right)=\left(\begin{array}{c}{f}_1\\ \left(1{\otimes }_A{f}_1\right)\oplus f_2\end{array}\right)$ .

2) $h\mathrm{<mo>\; :\; </mo>}A\text{-Mod}\times B\text{-Mod}\to T\text{-Mod}$ is defined as follows: for each object ( $M_1\mathrm{,}{M}_2$ ) of $A\text{-Mod}\times B\text{-Mod}$ , let $h\left(M_1\mathrm{,}{M}_2\right)=\left(\begin{array}{c}{M}_1\oplus {\text{Hom}}_B\left(U\mathrm{,}{M}_2\right)\\ M_2\end{array}\right)$ with the obvious map and for any morphism ( $f_1\mathrm{,}{f}_2$ ) in $A\text{-Mod}\times B\text{-Mod}$ , let $h\left(f_1\mathrm{,}{f}_2\right)=\left(\begin{array}{c}{f}_1\oplus {\text{Hom}}_B\left(U\mathrm{,}{f}_2\right)\\ f_2\end{array}\right)$ .

3) $q\mathrm{<mo>\; :\; </mo>}T\text{-Mod}\to A\text{-Mod}\times B\text{-Mod}$ is defined as follows: for each left T-module $\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)$ as $q\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)=\left(M_1\mathrm{,}{M}_2\right)$ , and for each morphism $\left(\begin{array}{c}{f}_1\\ f_2\end{array}\right)$ in T-Mod as $q\left(\begin{array}{c}{f}_1\\ f_2\end{array}\right)=\left(f_1\mathrm{,}{f}_2\right)$ .

Note that $p$ is a left adjoint of $q$ and $h$ is a right adjoint of $q$ . It is clear that $q$ is exact. $p$ , in particular, preserves projective objects, while $h$ preserves injective objects.

Between the category Mod-T and the product category $\text{Mod-}A\times \text{Mod-}B$ , there are similar functors $p\mathrm{,}q\mathrm{,}h$ .

Let $M={\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}\in T\text{-Mod}$ . By [6] , $M^{+}={\left(M_1^{+}\mathrm{,}{M}_2^{+}\right)}_{{\phi }_{M^{+}}}$ is the character right T-module of $M$ , where ${\phi }_{M^{+}}\mathrm{<mo>\; :\; </mo>}{M}_2^{+}{\otimes }_{B}U\to M_1^{+}$ is defined by ${\phi }_{M^{+}}\left(f\otimes u\right)\left(x\right)=f\left({\phi }^M\left(u\otimes x\right)\right)$ for any $f\in M_2^{+}$ , $u\in U$ and $x\in M_1$ .

2. Preliminaries

Definition 2.1. ([ [7] , Definition 2.1]) A $\left(R\mathrm{,}S\right)$ -bimodule C is called semidualizing if the following conditions are satisfied:

1) ${}_{R}C$ and $C_S$ permit a degreewise finite projective resolution in the corresponding module categories.

2) The natural homothety morphisms $R\to {\text{Hom}}_S\left(C\mathrm{,}C\right)$ and $S\to {\text{Hom}}_R\left(C\mathrm{,}C\right)$ are ring isomorphisms.

3) ${\text{Ext}}_R^{\ge 1}\left(C\mathrm{,}C\right)={\text{Ext}}_S^{\ge 1}\left(C\mathrm{,}C\right)=0$ .

Definition 2.2. ([ [8] , Section 3]) A Wakamatsu tilting module is a left R-module ${}_{R}C$ satisfying the following properties:

1) ${}_{R}C$ permits a degreewise finite projective resolution.

2) ${\text{Ext}}_R^{\ge 1}\left(C\mathrm{,}C\right)=0$ .

3) There exists a ${\text{Hom}}_R\left(-\mathrm{,}C\right)$ -exact exact sequence of R-modules

$X\mathrm{<mo>\; :\; </mo>0}\to R\to C^0\to C^1\to \cdots \mathrm{,}$

where $C^i\in {\text{add}}_R\left(C\right)$ for every $i\in \mathbb{N}$ .

By [ [8] , Corollary 3.2], ${}_R{C}_S$ is semidualizing if and only if ${}_{R}C$ is a Wakamatsu tilting module with $S\cong {\text{End}}_R\left(C\right)$ if and only if $C_S$ is a Wakamatsu tilting module with $R\cong {\text{End}}_S\left(C\right)$ .

Definition 2.3. ([ [9] , Definition 3.1]) Let $C,M\in R\text{-Mod}$ , M is said to be ${\mathcal{F}}_C$ -flat if $M^{+}$ belongs to the class ${\text{Prod}}_{R^{op}}\left(C^{+}\right)$ , and we will denote the class of all ${\mathcal{F}}_C$ -flat modules as ${\mathcal{F}}_C\left(R\right)$ .

When $C=R$ , ${\mathcal{F}}_C\left(R\right)=\mathcal{F}\left(R\right)$ . Thus $\mathcal{F}\left(R\right)$ is a special case of ${\mathcal{F}}_C\left(R\right)$ .

Remark 2.4. If ${}_R{C}_S$ is semidualizing, then ${\mathcal{F}}_C\left(R\right)=C{\otimes }_S\mathcal{F}\left(S\right)$ by [ [9] , Proposition 3.3].

Lemma 2.5. ([ [10] , Lemma 4]) Let $X={\left(\begin{array}{c}{X}_1\\ X_2\end{array}\right)}_{{\phi }^X}\in T\text{-Mod}$ and $\left(C_1\mathrm{,}{C}_2\right)\in A\text{-Mod}\times B\text{-Mod}$ .

$X\in {\text{Add}}_T\left(p\left(C_1\mathrm{,}{C}_2\right)\right)$ if and only if

1) $X\cong p\left(X_1\mathrm{,}\overline{X_2}\right)$ ;

2) $X_1\in {\text{Add}}_A\left(C_1\right)$ and $\overline{X_2}\in {\text{Add}}_B\left(C_2\right)$ .

In this instance, ${\phi }^X$ is injective.

Lemma 2.6. ([ [11] , Theorem 3.1]) Let $M={\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}\in T\text{-Mod}$ . $M\in \mathcal{P}\left(T\right)$ if and only if $M_1\in \mathcal{P}\left(A\right)$ , $\overline{M_2}\in \mathcal{P}\left(B\right)$ and ${\phi }^M$ is injective.

Lemma 2.7. Let $X={\left(X_1\mathrm{,}{X}_2\right)}_{{\phi }_X}\in \text{Mod-}T$ and $\left(C_1\mathrm{,}{C}_2\right)\in A\text{-Mod}\times B\text{-Mod}$ .

$X\in {\text{Prod}}_{T^{op}}\left(p^{+}\left(C_1\mathrm{,}{C}_2\right)\right)$ if and only if

1) $X\cong h\left(X_1\mathrm{,}\ker \left(\widetilde{{\phi }_X}\right)\right)$ ;

2) $X_1\in {\text{Prod}}_{A^{op}}\left(C_1^{+}\right)$ and $\ker \left(\widetilde{{\phi }_X}\right)\in {\text{Prod}}_{B^{op}}\left(C_2^{+}\right)$ .

In this instance, $\widetilde{{\phi }_X}$ is surjective.

Proof. “ $\Leftarrow$ ” If $X_1\in {\text{Prod}}_{A^{op}}\left(C_1^{+}\right)$ and $\ker \left(\widetilde{{\phi }_X}\right)\in {\text{Prod}}_{B^{op}}\left(C_2^{+}\right)$ , then $X_1\oplus {\Upsilon }_1={\left(C_1^{+}\right)}^{I_1}$ and $\ker \left(\widetilde{{\phi }_X}\right)\oplus {\Upsilon }_2={\left(C_2^{+}\right)}^{I_2}$ for some $\left({\Upsilon }_1\mathrm{,}{\Upsilon }_2\right)\in \text{Mod-}A\times \text{Mod-}B$ and some sets $I_1$ and $I_2$ . Without loss of generality, we can assume that $I=I_1=I_2$ . Then:

$\begin{array}{c}X\oplus h\left({\Upsilon }_1\mathrm{,}{\Upsilon }_2\right)\cong h\left(X_1\mathrm{,}\ker \left(\widetilde{{\phi }_X}\right)\right)\oplus h\left({\Upsilon }_1\mathrm{,}{\Upsilon }_2\right)\\ =\left(X_1\mathrm{,}{\text{Hom}}_{A^{op}}\left(U\mathrm{,}{X}_1\right)\oplus \ker \left(\widetilde{{\phi }_X}\right)\right)\oplus \left({\Upsilon }_1\mathrm{,}{\text{Hom}}_{A^{op}}\left(U\mathrm{,}{\Upsilon }_1\right)\oplus {\Upsilon }_2\right)\\ =\left({\left(C_1^{+}\right)}^I\mathrm{,}{\text{Hom}}_{A^{op}}\left(U\mathrm{,}{\left(C_1^{+}\right)}^I\right)\oplus {\left(C_2^{+}\right)}^I\right)\\ \cong \left({\left(C_1^{+}\right)}^I\mathrm{,}{\text{Hom}}_{A^{op}}{\left(U\mathrm{,}{C}_1^{+}\right)}^I\oplus {\left(C_2^{+}\right)}^I\right)\\ \cong \left({\left(C_1^{+}\right)}^I\mathrm{,}{\left({\left(U{\otimes }_A{C}_1\right)}^{+}\right)}^I\oplus {\left(C_2^{+}\right)}^I\right)\\ ={\left(p^{+}\left(C_1\mathrm{,}{C}_2\right)\right)}^I\mathrm{.}\end{array}$

Hence, $X\in {\text{Prod}}_{T^{op}}\left(p^{+}\left(C_1\mathrm{,}{C}_2\right)\right)$ .

“ $\Rightarrow$ ” Let $X\in {\text{Prod}}_{T^{op}}\left(p^{+}\left(C_1\mathrm{,}{C}_2\right)\right)$ and $\Upsilon ={\left({\Upsilon }_1\mathrm{,}{\Upsilon }_2\right)}_{{\phi }_{\Upsilon }}\in \text{Mod-}T$ such that $X\oplus \Upsilon ={\left(p^{+}\left(C_1\mathrm{,}{C}_2\right)\right)}^I$ for some set I. Then $\widetilde{{\phi }_X}$ is surjective as X is a submodule of ${\left(p^{+}\left(C_1\mathrm{,}{C}_2\right)\right)}^I$ and $\widetilde{{\phi }_{C^{+}}}$ is surjective. Now, let $C\mathrm{<mo>\; :\; </mo>}=p\left(C_1\mathrm{,}{C}_2\right)$ , there is an exact split sequence:

$0\to \Upsilon \stackrel{\left({\lambda }_1\mathrm{,}{\lambda }_2\right)}{\to }{\left(C^{+}\right)}^I\stackrel{\left(p_1\mathrm{,}{p}_2\right)}{\to }X\to \mathrm{0,}$

which induces the following commutative diagram with exact rows and columns:

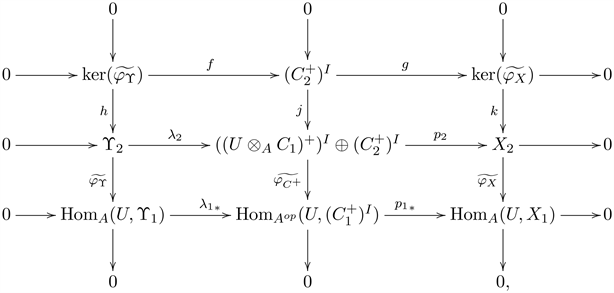
where $h,j,k$ are the canonical injections. Clearly, $p_1$ and $p_1{}_{\mathrm{<mo>\; *\; </mo>}}$ are split epimorphisms. Thus, $X_1\in {\text{Prod}}_{A^{op}}\left(C_1^{+}\right)$ . Next, we prove that the short exact sequence:

$0\to \ker \left(\widetilde{{\phi }_X}\right)\stackrel{k}{\to }{X}_2\stackrel{\widetilde{{\phi }_X}}{\to }{\text{Hom}}_A\left(U\mathrm{,}{X}_1\right)\to 0$

splits. Let r be the retraction of $p_1^{\mathrm{<mo>\; *\; </mo>}}$ . If $i\mathrm{<mo>\; :\; </mo>}{\text{Hom}}_{A^{op}}\left(U\mathrm{,}{\left(C_1^{+}\right)}^I\right)\to {\left({\left(U{\otimes }_A{C}_1\right)}^{+}\right)}^I\oplus {\left(C_2^{+}\right)}^I$ denotes the canonical injection by ${\text{Hom}}_{A^{op}}\left(U\mathrm{,}\left(C_1^{+}\right)\right)\cong {\left(U{\otimes }_A{C}_1\right)}^{+}$ , then $\widetilde{{\phi }_X}{p}_{2}ir=p_1{}_{\mathrm{<mo>\; *\; </mo>}}\widetilde{{\phi }_{C^{+}}}ir=p_1{}_{\mathrm{<mo>\; *\; </mo>}}r=1_{{\text{Hom}}_A\left(U\mathrm{,}{X}_1\right)}$ . Thus $X_2\cong {\text{Hom}}_A\left(U,X_1\right)\oplus \ker \left(\widetilde{{\phi }_X}\right)$ and the first row is a split exact sequence too. So $\ker \left(\widetilde{{\phi }_X}\right)\in {\text{Prod}}_{B^{op}}\left(C_2^{+}\right)$ and $X\cong h\left(X_1,\ker \left(\widetilde{{\phi }_X}\right)\right)$ .¨

Corollary 2.8. Let $X={\left(\begin{array}{c}{X}_1\\ X_2\end{array}\right)}_{{\phi }^X}\in T\text{-Mod}$ and $\left(C_1\mathrm{,}{C}_2\right)\in A\text{-Mod}\times B\text{-Mod}$ .

If $C=p\left(C_1\mathrm{,}{C}_2\right)$ , then $X\in {\mathcal{F}}_C\left(T\right)$ if and only if

1) $X^{+}\cong h\left(X_1^{+}\mathrm{,}{\bar{X}}_2^{+}\right)$ ;

2) $X_1\in {\mathcal{F}}_{C_1}\left(A\right)$ and ${\bar{X}}_2\in {\mathcal{F}}_{C_2}\left(B\right)$ .

In this instance, ${\phi }^X$ is injective.

Proof. $X\in {\mathcal{F}}_C\left(T\right)$ if and only if $X^{+}={\left(X_1^{+}\mathrm{,}{X}_2^{+}\right)}_{{\phi }_{X^{+}}}\in {\text{Prod}}_{T^{op}}\left(C^{+}\right)$ if and only if $X^{+}\cong h\left(X_1^{+},\ker \left(\widetilde{{\phi }_{X^{+}}}\right)\right)$ , $X_1^{+}\in {\text{Prod}}_{A^{op}}\left(C_1^{+}\right)$ , $\ker \left(\widetilde{{\phi }_{X^{+}}}\right)\in {\text{Prod}}_{B^{op}}\left(C_2^{+}\right)$ by Lemma 2.7. Note that $\widetilde{{\phi }_{X^{+}}}$ is surjective. Hence, ${\phi }^X$ is injective. Then we get an exact sequence

$0\to U{\otimes }_A{X}_1\stackrel{{\phi }^X}{\to }{X}_2\to {\bar{X}}_2\to 0.$

Consider the commutative diagram with exact rows shown below.

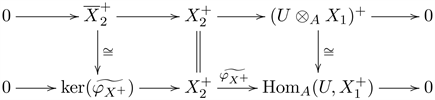
Thus ${\bar{X}}_2^{+}\cong \ker \left(\widetilde{{\phi }_{X^{+}}}\right)\in {\text{Prod}}_{B^{op}}\left(C_2^{+}\right)$ . So $X\in {\mathcal{F}}_C\left(T\right)$ if and only if $X^{+}\cong h\left(X_1^{+}\mathrm{,}{\bar{X}}_2^{+}\right)$ , $X_1\in {\mathcal{F}}_{C_1}\left(A\right)$ and ${\bar{X}}_2\in {\mathcal{F}}_{C_2}\left(B\right)$ , and the proof is finished.

3. Relative Ding Projective Modules

This section will characterize relative Ding projective modules over a formal triangular matrix ring.

Definition 3.1 ([ [12] , Definition 1.1]) Let ${}_R{C}_S$ be a semidualizing bimodule. A left R-module M is said to be $D_C$ -projective if there exists a ${\text{Hom}}_R\left(-\mathrm{,}C{\otimes }_{S}F\right)$ -exact exact sequence in R-Mod:

$\cdots \to P_1\to P_0\to A^0\to A^1\to \cdots$

with $A^i\in {\text{Add}}_R\left(C\right)$ , $P_i\in \mathcal{P}\left(R\right)$ for every $i\in \mathbb{N}$ and $F\in \mathcal{F}\left(S\right)$ , such that $M\cong \mathrm{Im}\left(P_0\to A^0\right)$ .

The class of all $D_C$ -projective R-modules is denoted by $D_{C}P\left(R\right)$ .

Note that if $C=R$ , then $D_C$ -projective R-modules are Ding projective R-modules.

We introduce the following concept, which is critical to the rest of this study, inspired by the definition of C-compatible bimodule in [ [10] , Definition 4].

Definition 3.2. Let $\left(C_1\mathrm{,}{C}_2\right)\in A\text{-Mod}\times B\text{-Mod}$ and $C=p\left(C_1\mathrm{,}{C}_2\right)$ . A bimodule ${}_B{U}_A$ is said to be Ding C-compatible if the following two conditions hold:

(a) The complex $U{\otimes }_A{X}_1$ is exact for every exact sequence in A-Mod:

$X_1\mathrm{<mo>\; :\; </mo>}\cdots \to P_1^1\to P_1^0\to A_1^0\to A_1^1\to \cdots$

with $P_1^i\in \mathcal{P}\left(A\right)$ and $A_1^i\in {\text{Add}}_A\left(C_1\right)$ for every $i\in \mathbb{N}$ .

(b) The complex ${\text{Hom}}_B\left(X_2\mathrm{,}U{\otimes }_A{\mathcal{F}}_{C_1}\left(A\right)\right)$ is exact for every ${\text{Hom}}_B\left(-\mathrm{,}{\mathcal{F}}_{C_2}\left(B\right)\right)$ -exact exact sequence in B-Mod:

$X_2\mathrm{<mo>\; :\; </mo>}\cdots \to P_2^1\to P_2^0\to A_2^0\to A_2^1\to \cdots$

with $P_2^i\in \mathcal{P}\left(B\right)$ and $A_2^i\in {\text{Add}}_B\left(C_2\right)$ for every $i\in \mathbb{N}$ .

Furthermore, U is said to be weakly Ding C-compatible if it meets (b) and the following condition:

(a') The complex $U{\otimes }_A{X}_1$ is exact for every ${\text{Hom}}_A\left(-\mathrm{,}{\mathcal{F}}_{C_1}\left(A\right)\right)$ -exact exact sequence in A-Mod:

$X_1\mathrm{<mo>\; :\; </mo>}\cdots \to P_1^1\to P_1^0\to A_1^0\to A_1^1\to \cdots$

with $P_1^i\in \mathcal{P}\left(A\right)$ and $A_1^i\in {\text{Add}}_A\left(C_1\right)$ for every $i\in \mathbb{N}$ .

Proposition 3.3. Suppose that $C=p\left(C_1\mathrm{,}{C}_2\right)$ be a left T-module and U be weakly Ding C-compatible. If ${}_A{C}_1$ and ${}_B{C}_2$ are semidualizing, then $p\left(C_1\mathrm{,}{C}_2\right)$ is semidualizing.

Proof. Assume that ${}_A{C}_1$ and ${}_B{C}_2$ are semidualizing. By [ [8] , Corollary 3.2], ${}_A{C}_1$ and ${}_B{C}_2$ are tilting. To prove C is tilting, the functor $p$ preserves finitely generated modules by [13] . Then ${\text{Ext}}_A^{i\ge 1}\left(C_1\mathrm{,}{C}_1\right)=0$ and ${\text{Ext}}_B^{i\ge 1}\left(C_2\mathrm{,}{C}_2\right)=0$ . Observe that $C_1\in D_{C_1}P\left(A\right)$ and $C_2\in D_{C_2}P\left(B\right)$ by [ [12] , Proposition 1.8]. Since U satisfies (a'), ${\text{Tor}}_{i\ge 1}^A\left(U\mathrm{,}{C}_1\right)=0$ . And, as U satisfies (b), ${\text{Ext}}_B^{i\ge 1}\left(C_2\mathrm{,}U{\otimes }_A{C}_1\right)=0$ . For every $n\ge 1$ , by [ [10] , Lemma 3], we get that:

$\begin{array}{c}{\text{Ext}}_T^n\left(C\mathrm{,}C\right)={\text{Ext}}_T^n\left(p\left(C_1\mathrm{,}{C}_2\right)\mathrm{,}p\left(C_1\mathrm{,}{C}_2\right)\right)\\ \cong {\text{Ext}}_A^n\left(C_1\mathrm{,}{C}_1\right)\oplus {\text{Ext}}_B^n\left(C_2\mathrm{,}U{\otimes }_A{C}_1\right)\oplus {\text{Ext}}_B^n\left(C_2\mathrm{,}{C}_2\right)\\ =0.\end{array}$

Furthermore, there exist exact sequences:

$X_1\mathrm{<mo>\; :\; </mo>0}\to A\to C_1^0\to C_1^1\to \cdots \mathrm{,}$

and:

$X_2\mathrm{<mo>\; :\; </mo>0}\to B\to C_2^0\to C_2^1\to \cdots$

which are ${\text{Hom}}_A\left(-\mathrm{,}{\text{Add}}_A\left(C_1\right)\right)$ -exact and ${\text{Hom}}_B\left(-\mathrm{,}{\text{Add}}_B\left(C_1\right)\right)$ -exact, respectively, and $C_1^i\in {\text{add}}_A\left(C_1\right)$ , $C_2^i\in {\text{add}}_B\left(C_2\right)$ , $\forall i\in \mathbb{N}$ . Note that every cokernel in $X_1$ and $X_2$ are finitely presented. Thus, ${\text{Hom}}_A\left(X_1\mathrm{,}{\mathcal{F}}_{C_1}\left(A\right)\right)$ and ${\text{Hom}}_A\left(X_2\mathrm{,}{\mathcal{F}}_{C_2}\left(B\right)\right)$ are exact. Since U is weakly Ding C-compatible, the complex $U{\otimes }_A{X}_1$ is exact. As a result, we get the following exaxt sequence

$p\left(X_1\mathrm{,}{X}_2\right)\mathrm{<mo>\; :\; </mo>0}\to T\to p\left(C_1^0\mathrm{,}{C}_2^0\right)\to p\left(C_1^1\mathrm{,}{C}_2^1\right)\to \cdots \mathrm{,}$

with $p\left(C_1^i\mathrm{,}{C}_2^i\right)=\left(\begin{array}{c}{C}_1^i\\ U{\otimes }_A{C}_1^i\oplus C_2^i\end{array}\right)\in {\text{add}}_T\left(p\left(C_1\mathrm{,}{C}_2\right)\right)$ , $\forall i\in \mathbb{N}$ , by Lemma 2.5.

Let $X\in {\text{Add}}_T\left(C\right)$ , by Lemma 2.5, $X\cong p\left(X_1\mathrm{,}{X}_2\right)$ where $X_1\in {\text{Add}}_A\left(C_1\right)$ and $X_2\in {\text{Add}}_B\left(C_2\right)$ . There is a complex isomorphism using adjointness ( $p\mathrm{,}q$ ):

${\text{Hom}}_T\left(p\left(X_1\mathrm{,}{X}_2\right)\mathrm{,}X\right)\cong {\text{Hom}}_A\left(X_1\mathrm{,}{X}_1\right)\oplus {\text{Hom}}_B\left(X_2\mathrm{,}U{\otimes }_A{X}_1\right)\oplus {\text{Hom}}_B\left(X_2\mathrm{,}{X}_2\right)\mathrm{.}$

It should be noted that the complexes ${\text{Hom}}_A\left(X_1\mathrm{,}{X}_1\right)$ and ${\text{Hom}}_B\left(X_2\mathrm{,}{X}_2\right)$ , as well as the complex ${\text{Hom}}_B\left(X_2\mathrm{,}U{\otimes }_A{X}_1\right)$ are exact since U is weakly Ding C-compatible. Then ${\text{Hom}}_T\left(p\left(X_1\mathrm{,}{X}_2\right)\mathrm{,}X\right)$ is exact. So $p\left(C_1\mathrm{,}{C}_2\right)$ is semidualizing by [ [8] , Corollary 3.2].¨

Lemma 3.4. Assume that ${}_A{C}_1$ and ${}_B{C}_2$ are semidualizing. Let $C=p\left(C_1\mathrm{,}{C}_2\right)$ be a left T-module and U be weakly Ding C-compatible.

1) If $M_1\in D_{C_1}P\left(A\right)$ , then $p\left(M_1\mathrm{,0}\right)\in D_{C}P\left(T\right)$ .

2) If $M_2\in D_{C_2}P\left(B\right)$ , then $p\left(\mathrm{0,}{M}_2\right)\in D_{C}P\left(T\right)$ .

Proof. By Proposition 3.3, the functor $p$ preservers semidualizing. Thus $C{\otimes }_{S}F\cong {\mathcal{F}}_C\left(T\right)$ by Remark 2.4.

1) Assume that $M_1\in D_{C_1}P\left(A\right)$ . There exists a ${\text{Hom}}_A\left(-\mathrm{,}{\mathcal{F}}_{C_1}\left(A\right)\right)$ -exact exact sequence in A-Mod:

$X_1\mathrm{<mo>\; :\; </mo>}\cdots \to P_1^1\to P_1^0\to C_1^0\to C_1^1\to \cdots \mathrm{,}$

where $P_1^i\in \mathcal{P}\left(A\right)$ and $C_1^i\in {\text{Add}}_A\left(C_1\right)$ $\forall i\in \mathbb{N}$ and $M_1\cong \mathrm{Im}\left(P_1^0\to C_1^0\right)$ . Since U is weakly Ding C-compatible, we have the complex $U{\otimes }_A{X}_1$ is exact in B-Mod. So we get an exact sequence

$p\left(X_1\mathrm{,0}\right)\mathrm{<mo>\; :\; </mo>}\cdots \to \left(\begin{array}{c}{P}_1^1\\ U{\otimes }_A{P}_1^1\end{array}\right)\to \left(\begin{array}{c}{P}_1^0\\ U{\otimes }_A{P}_1^0\end{array}\right)\to \left(\begin{array}{c}{C}_1^0\\ U{\otimes }_A{C}_1^0\end{array}\right)\to \left(\begin{array}{c}{C}_1^1\\ U{\otimes }_A{C}_1^1\end{array}\right)\to \cdots$

with

$\left(\begin{array}{c}{M}_1\\ U{\otimes }_A{M}_1\end{array}\right)\cong \mathrm{Im}\left(\left(\begin{array}{c}{P}_1^0\\ U{\otimes }_A{P}_1^0\end{array}\right)\to \left(\begin{array}{c}{C}_1^0\\ U{\otimes }_A{C}_1^0\end{array}\right)\right).$

Clearly, $p\left(P_1^i\mathrm{,0}\right)=\left(\begin{array}{c}{P}_1^i\\ U{\otimes }_A{P}_1^i\end{array}\right)\in \mathcal{P}\left(T\right)$ and $p\left(C_1^i\mathrm{,0}\right)=\left(\begin{array}{c}{C}_1^i\\ U{\otimes }_A{C}_1^i\end{array}\right)\in {\text{Add}}_T\left(C\right)$ for every $i\in \mathbb{N}$ by Lemmas 2.6 and 2.5.

If $N={\left(\begin{array}{c}{N}_1\\ N_2\end{array}\right)}_{{\phi }^N}\in {\mathcal{F}}_C\left(T\right)$ , then $N_1\in {\mathcal{F}}_{C_1}\left(A\right)$ by Corollary 2.8. Then using the adjointness, we get that ${\text{Hom}}_T\left(p\left(X_1\mathrm{,0}\right)\mathrm{,}N\right)\cong {\text{Hom}}_A\left(X_1\mathrm{,}{N}_1\right)$ is exact. Thus $\left(\begin{array}{c}{M}_1\\ U{\otimes }_A{M}_1\end{array}\right)$ is $D_C$ -projective.

2) Assume that $M_2\in D_{C_2}P\left(B\right)$ . There exists a ${\text{Hom}}_B\left(-\mathrm{,}{\mathcal{F}}_{C_2}\left(B\right)\right)$ -exact exact sequence in B-Mod:

$X_2\mathrm{<mo>\; :\; </mo>}\cdots \to P_2^1\to P_2^0\to C_2^0\to C_2^1\to \cdots \mathrm{,}$

where $P_2^i\in \mathcal{P}\left(B\right)$ and $C_2^i\in {\text{Add}}_B\left(C_2\right)$ $\forall i\in \mathbb{N}$ and $M_2\cong \mathrm{Im}\left(P_2^0\to C_2^0\right)$ . As a result, we have an exact sequence

$p\left(\mathrm{0,}{X}_2\right)\mathrm{<mo>\; :\; </mo>}\cdots \to \left(\begin{array}{c}0\\ P_2^1\end{array}\right)\to \left(\begin{array}{c}0\\ P_2^0\end{array}\right)\to \left(\begin{array}{c}0\\ C_2^0\end{array}\right)\to \left(\begin{array}{c}0\\ C_2^1\end{array}\right)\to \cdots$

with $\left(\begin{array}{c}0\\ M_2\end{array}\right)\cong \mathrm{Im}\left(\left(\begin{array}{c}0\\ P_2^0\end{array}\right)\to \left(\begin{array}{c}0\\ C_2^0\end{array}\right)\right)$ , $p\left(\mathrm{0,}{P}_2^i\right)=\left(\begin{array}{c}0\\ P_2^i\end{array}\right)\in \mathcal{P}\left(T\right)$ and $p\left(\mathrm{0,}{C}_2^i\right)=\left(\begin{array}{c}0\\ C_2^i\end{array}\right)\in {\text{Add}}_T\left(C\right)$ for every $i\in \mathbb{N}$ by Lemmas 2.6 and 2.5 respectively. Let $N={\left(\begin{array}{c}{N}_1\\ N_2\end{array}\right)}_{{\phi }^N}\in {\mathcal{F}}_C\left(T\right)$ , then $N_1\in {\mathcal{F}}_{C_1}\left(A\right)$ , ${\bar{N}}_2\in {\mathcal{F}}_{C_2}\left(B\right)$ and ${\phi }^N$ is injective by Corollary 2.8. Thus we obtain a short exact sequence:

$0\to U{\otimes }_A{N}_1\to N_2\to {\bar{N}}_2\to 0.$

Because U is weakly Ding C-compatible, $\cdots \to P_2^1\to P_2^0\to M_2\to 0$ is a ${\text{Hom}}_B\left(-\mathrm{,}U{\otimes }_A{N}_1\right)$ -exact exact sequence. Then ${\text{Ext}}_B^1\left(M_2\mathrm{,}U{\otimes }_A{N}_1\right)=0$ . Consider a short exact sequence $0\to M_2\to C_2^0\to L\to 0$ with $L\cong \mathrm{Im}\left(M_2\to C_2^0\right)$ is $D_{C_2}$ -projective by [ [12] , Proposition 1.13]. Thus ${\text{Ext}}_B^1\left(L\mathrm{,}U{\otimes }_A{N}_1\right)=0$ , and then ${\text{Ext}}_B^1\left(C_2^0\mathrm{,}U{\otimes }_A{N}_1\right)=0$ . Consequently, ${\text{Ext}}_B^1\left(C_2^i\mathrm{,}U{\otimes }_A{N}_1\right)=0$ . Then we obtain the exact sequence of complexes shown below.

$0\to {\text{Hom}}_B\left(X_2,U{\otimes }_A{N}_1\right)\to {\text{Hom}}_B\left(X_2,N_2\right)\to {\text{Hom}}_B\left(X_2,{\bar{N}}_2\right)\to 0$

As U is weakly Ding C-compatible, ${\text{Hom}}_B\left(X_2,U{\otimes }_A{N}_1\right)$ is exact and ${\text{Hom}}_B\left(X_2,{\bar{N}}_2\right)$ is exact. Thus ${\text{Hom}}_B\left(X_2,N_2\right)$ is exact. Then ${\text{Hom}}_T\left(p\left(\mathrm{0,}{X}_2\right)\mathrm{,}N\right)\cong {\text{Hom}}_B\left(X_2\mathrm{,}{N}_2\right)$ is exact. Above all, $p\left(\mathrm{0,}{M}_2\right)\in D_{C}P\left(T\right)$ .

Theorem 3.5. Assume that ${}_A{C}_1$ and ${}_B{C}_2$ are semidualizing. Let $M={\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}$ , $C=p\left(C_1\mathrm{,}{C}_2\right)\in T\text{-Mod}$ and U be Ding C-compatible. Then the following statements are equivalent:

1) M is $D_C$ -projective.

2) ${\phi }^M$ is injective, $M_1$ is $D_{C_1}$ -projective and ${\bar{M}}_2\mathrm{<mo>\; :\; </mo>}=\text{Coker}{\phi }^M$ is $D_{C_2}$ -projective.

In this instance, $U{\otimes }_A{M}_1$ is $D_{C_2}$ -projective if and only if $M_2$ is $D_{C_2}$ -projective.

Proof. (1) $\Rightarrow$ (2) There exists a ${\text{Hom}}_T\left(-\mathrm{,}{\mathcal{F}}_C\left(T\right)\right)$ -exact exact sequence in T-Mod:

$X=\cdots \to {\left(\begin{array}{c}{P}_1^1\\ P_2^1\end{array}\right)}_{{\phi }^{P^1}}\to {\left(\begin{array}{c}{P}_1^0\\ P_2^0\end{array}\right)}_{{\phi }^{P^0}}\to {\left(\begin{array}{c}{C}_1^0\\ C_2^0\end{array}\right)}_{{\phi }^{C^0}}\to {\left(\begin{array}{c}{C}_1^1\\ C_2^1\end{array}\right)}_{{\phi }^{C^1}}\to \cdots \mathrm{,}$

where $P^i={\left(\begin{array}{c}{P}_1^i\\ P_2^i\end{array}\right)}_{{\phi }^{P^i}}\in \mathcal{P}\left(T\right)$ and $C^i={\left(\begin{array}{c}{C}_1^i\\ C_2^i\end{array}\right)}_{{\phi }^{C^i}}\in {\text{Add}}_T\left(C\right)$ $\forall i\in \mathbb{N}$ , and such that $M\cong \mathrm{Im}\left(P^0\to C^0\right)$ . Then we get an exact sequence in A-Mod:

$X_1:\cdots \to P_1^1\to P_1^0\to C_1^0\to C_1^1\to \cdots \mathrm{,}$

where $P_1^i\in \mathcal{P}\left(A\right)$ and $C_1^i\in {\text{Add}}_A\left(C_1\right)$ $\forall i\in \mathbb{N}$ by Lemmas 2.6 and 2.5 and such that $M_1\cong \mathrm{Im}\left(P_1^0\to C_1^0\right)$ . As U is Ding C-compatible, the complex $U{\otimes }_A{X}_1$ is exact with $U{\otimes }_A{M}_1\cong \mathrm{Im}\left(U{\otimes }_A{P}_1^0\to U{\otimes }_A{C}_1^0\right)$ . Let $l_1\mathrm{<mo>\; :\; </mo>}{M}_1\to C_1^0$ and $l_2\mathrm{<mo>\; :\; </mo>}{M}_2\to C_2^0$ be the inclusions, then $1_U\otimes l_1$ is injective. Consequently, the commutative diagram is as follows:

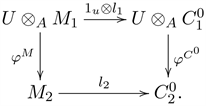
According to Lemma 2.5, ${\phi }^{C^0}$ is injective, then ${\phi }^M$ will be as well. Furthermore, for every $i\in \mathbb{N}$ , ${\phi }^{C^i}$ and ${\phi }^{P^i}$ are injective by Lemmas 2.5 and 2.6. The result is the commutative diagram with exact columns shown below.

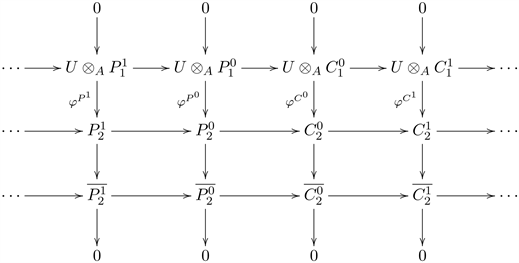
Since the first and the second rows are exact in the above diagram, we get an exact sequence in B-Mod:

${\bar{X}}_2\mathrm{<mo>\; :\; </mo>}\cdots \to \overline{P_2^1}\to \overline{P_2^0}\to \overline{C_2^0}\to \overline{C_2^1}\to \cdots \mathrm{,}$

where $\overline{P_2^i}\in \mathcal{P}\left(B\right)$ and $\overline{C_2^i}\in {\text{Add}}_B\left(C_2\right)$ for every $i\in \mathbb{N}$ by Lemmas 2.6 and 2.5, and such that ${\bar{M}}_2\cong \mathrm{Im}\left(\overline{P_2^0}\to \overline{C_2^0}\right)$ . Let $N_1\in {\mathcal{F}}_{C_1}\left(A\right)$ and $N_2\in {\mathcal{F}}_{C_2}\left(B\right)$ , then $p\left(N_1\mathrm{,0}\right)\in {\mathcal{F}}_C\left(T\right)$ and $p\left(\mathrm{0,}{N}_2\right)\in {\mathcal{F}}_C\left(T\right)$ by Corollary 2.8. Then by using adjointness, ${\text{Hom}}_T\left(X\mathrm{,}p\left(\mathrm{0,}{N}_2\right)\right)\cong {\text{Hom}}_B\left({\bar{X}}_2\mathrm{,}{N}_2\right)$ is exact. Thus, ${\bar{M}}_2$ is $D_{C_2}$ -projective. Note that $C^i\cong p\left(C_1^i\mathrm{,}\overline{C_2^i}\right)$ by Lemma 2.5. Then ${\text{Ext}}_T^1\left(C_i\mathrm{,}\left(\begin{array}{c}0\\ U{\otimes }_A{N}_1\end{array}\right)\right)\cong {\text{Ext}}_B^1\left(\overline{C_2^i}\mathrm{,}U{\otimes }_A{N}_1\right)=0$ by [ [10] , Lemma 3] and U is Ding C-compatible. As a result, when we apply the functor ${\text{Hom}}_T\left(X\mathrm{,}-\right)$ to the sequence:

$0\to \left(\begin{array}{c}0\\ U{\otimes }_A{N}_1\end{array}\right)\to \left(\begin{array}{c}{N}_1\\ U{\otimes }_A{N}_1\end{array}\right)\to \left(\begin{array}{c}{N}_1\\ 0\end{array}\right)\to \mathrm{0,}$

we get the exact sequence of complexes:

$0\to {\text{Hom}}_T\left(X\mathrm{,}\left(\begin{array}{c}0\\ U{\otimes }_A{N}_1\end{array}\right)\right)\to {\text{Hom}}_T\left(X\mathrm{,}\left(\begin{array}{c}{N}_1\\ U{\otimes }_A{N}_1\end{array}\right)\right)\to {\text{Hom}}_T\left(X\mathrm{,}\left(\begin{array}{c}{N}_1\\ 0\end{array}\right)\right)\to 0.$

By applying adjointness, we obtain that

${\text{Hom}}_T\left(X\mathrm{,}\left(\begin{array}{c}0\\ U{\otimes }_A{N}_1\end{array}\right)\right)\cong {\text{Hom}}_B\left({\bar{X}}_2\mathrm{,}U{\otimes }_A{N}_1\right)$

and

${\text{Hom}}_T\left(X\mathrm{,}\left(\begin{array}{c}{N}_1\\ 0\end{array}\right)\right)\cong {\text{Hom}}_A\left(X_1\mathrm{,}{N}_1\right)\mathrm{.}$

Note that ${\text{Hom}}_T\left(X\mathrm{,}\left(\begin{array}{c}{N}_1\\ U{\otimes }_A{N}_1\end{array}\right)\right)$ is exact, and since U is Ding C-compatible, ${\text{Hom}}_B\left({\bar{X}}_2\mathrm{,}U{\otimes }_A{N}_1\right)$ is exact too. It implies that ${\text{Hom}}_A\left(X_1\mathrm{,}{N}_1\right)$ is exact. So $M_1$ is $D_{C_1}$ -projective.

2) $\Rightarrow$ 1) Because ${\phi }^M$ is injective, an exact sequence exists in T-Mod:

$0\to \left(\begin{array}{c}{M}_1\\ U{\otimes }_A{M}_1\end{array}\right)\to M\to \left(\begin{array}{c}0\\ {\bar{M}}_2\end{array}\right)\to 0.$

By Theorem 3.5, $\left(\begin{array}{c}{M}_1\\ U{\otimes }_A{M}_1\end{array}\right)$ and $\left(\begin{array}{c}0\\ {\bar{M}}_2\end{array}\right)$ are $D_C$ -projective T-modules. Hence, M is $D_C$ -projective according to [ [12] , Theorem 1.12]. Finally, there exists an exact sequence

$0\to U{\otimes }_A{M}_1\stackrel{{\phi }^M}{\to }{M}_2\to {\bar{M}}_2\to 0.$

Since ${\bar{M}}_2$ is $D_{C_2}$ -projective, $U{\otimes }_A{M}_1$ is $D_{C_2}$ -projective if and only if $M_2$ is $D_{C_2}$ -projective by [ [12] , Theorem 2.12].

Corollary 3.6. Assume that ${}_R{C}_1$ is semidualizing. Let R be a ring, $T\left(R\right)=\left(\begin{array}{cc}R& 0\\ R& R\end{array}\right)$ , $C=p\left(C_1\mathrm{,}{C}_1\right)$ and $M={\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}$ be a left $T\left(R\right)$ -module, then the following conditions are equivalent:

1) M is a $D_C$ -projective left T(R)-module.

2) $M_1$ and ${\bar{M}}_2$ is $D_{C_1}$ -projective, and ${\phi }^M$ is injective.

3) $M_1$ and $M_2$ is $D_{C_1}$ -projective, and ${\phi }^M$ is injective.

Proof. It is an immediate consequence of Theorem 3.5.¨

4. Relative Ding Projective Dimension

This section aims to search in the $D_C$ -projective dimension of T-modules as well as the left $D_C$ -projective global dimension of T. We now recall [12] that the concept of relative Ding projective dimenion. The $D_C$ -projective dimension $D_C$ -pd(M) of a left R-module M is defined as inf{n| there there is an exact sequence

$0\to D_n\to \cdots \to D_1\to D_0\to M\to 0$

with $D_i\in D_{C}P\left(R\right)$ for every $i\in \left\{\mathrm{0,}\cdots \mathrm{,}n\right\}$ . The left global $D_C$ -projective dimension of R is defined as: $D_C\text{-}PD\left(R\right)=\sup \left\{D_C\text{-}pd\left(M\right)\mathrm{<mo>\; |\; </mo>}M\in R\text{-Mod}\right\}$ .

Lemma 4.1. Assume that ${}_A{C}_1$ and ${}_B{C}_2$ are semidualizing. Let $C=p\left(C_1\mathrm{,}{C}_2\right)$ and U Ding C-compatible. Then the following statements hold.

1) $D_{C_2}\text{-}pd\left(M_2\right)=D_C\text{-}pd\left(\left(\begin{array}{c}0\\ M_2\end{array}\right)\right)$ .

2) $D_{C_1}\text{-}pd\left(M_2\right)\le D_C\text{-}pd\left(p\left(M_1\mathrm{,0}\right)\right)$ , and the equality is true if ${\text{Tor}}_{i\ge 1}^A\left(U\mathrm{,}{M}_1\right)=0$ .

Proof. 1) Consider the following exact sequence

$0\to K_2^n\to D_2^{n-1}\to \cdots \to D_2^0\to M_2\to 0$

with $D_2^i$ is $D_{C_2}$ -projective. As a result, we have an exact sequence in T-Mod:

$0\to \left(\begin{array}{c}0\\ K_2^n\end{array}\right)\to \left(\begin{array}{c}0\\ D_2^{n-1}\end{array}\right)\to \cdots \to \left(\begin{array}{c}0\\ D_2^0\end{array}\right)\to \left(\begin{array}{c}0\\ M_2\end{array}\right)\to 0$

with $\left(\begin{array}{c}0\\ D_2^i\end{array}\right)$ $D_C$ -projective by Theorem 3.5. Furthermore, by Theorem 3.5, $\left(\begin{array}{c}0\\ K_2^n\end{array}\right)$ is $D_C$ -projective if and only if $K_2^n$ is $D_{C_1}$ -projective. This means that $D_C\text{-}pd\left(\left(\begin{array}{c}0\\ M_2\end{array}\right)\right)\le n$ if and only if $D_{C_2}\text{-}pd\left(M_2\right)\le n$ by [ [12] , Theorem 2.4].

2) We may assume that $D_C\text{-}pd\left(\left(\begin{array}{c}{M}_1\\ U{\otimes }_A{M}_1\end{array}\right)\right)=m<\infty$ . There exists an exact sequence in T-Mod:

$0\to D^m\to D^{m-1}\to \cdots \to D^0\to \left(\begin{array}{c}{M}_1\\ U{\otimes }_A{M}_1\end{array}\right)\to 0$

with $D^i={\left(\begin{array}{c}{D}_1^i\\ D_2^i\end{array}\right)}_{{\phi }^{D^i}}\in D_{C}P\left(T\right)$ . Then there is an exact sequence

$0\to D_1^m\to D_1^{m-1}\to \cdots \to D_1^0\to M_1\to 0$

with $D_1^i\in D_{C_1}P\left(A\right)$ by Theorem 3.5. Thus $D_{C_1}\text{-}pd\left(M_1\right)\le m$ .

In contrast, we demonstrate that $D_C\text{-}pd\left(\left(\begin{array}{c}{M}_1\\ U{\otimes }_A{M}_1\end{array}\right)\right)\le D_{C_1}\text{-}pd\left(M_1\right)$ when ${\text{Tor}}_{i\ge 1}^A\left(U\mathrm{,}{M}_1\right)=0$ . We may assume that $D_{C_1}\text{-}pd\left(M_1\right)=m<\infty$ . So there is an exact sequence

$X_1\mathrm{<mo>\; :\; </mo>0}\to K_1^m\to P_1^{m-1}\to \cdots \to P_1^0\to M_1\to 0$

with $P_1^i\in \mathcal{P}\left(A\right)$ . As a result, the complex $U\otimes X_1$ is exact and each $P_1^i$ is $D_{C_1}$ -projective by [ [12] , Proposition 1.8], and then, $K_1^m$ is $D_{C_1}$ -projective by [ [12] , Theorem 2.4]. So there is an exact sequence

$0\to \left(\begin{array}{c}{K}_1^m\\ U{\otimes }_A{K}_1^m\end{array}\right)\to \left(\begin{array}{c}{P}_1^{m-1}\\ U{\otimes }_A{P}_1^{m-1}\end{array}\right)\to \cdots \to \left(\begin{array}{c}{P}_1^0\\ U{\otimes }_A{P}_1^0\end{array}\right)\to \left(\begin{array}{c}{M}_1\\ U{\otimes }_A{M}_1\end{array}\right)\to 0.$

We obtain that $\left(\begin{array}{c}{K}_1^m\\ U{\otimes }_A{K}_1^m\end{array}\right)$ and all $\left(\begin{array}{c}{P}_1^i\\ U{\otimes }_A{P}_1^i\end{array}\right)$ are $D_C$ -projective by Theorem 3.5. Thus we get $D_C\text{-}pd\left(\left(\begin{array}{c}{M}_1\\ U{\otimes }_A{M}_1\end{array}\right)\right)\le m=D_{C_1}\text{-}pd\left(M_1\right)$ .

Inspired by the strong notion of the $G_{C_2}$ -projective global dimension of B in [10] for estimating the $G_C$ -projective dimension of a T-module and the left global $G_C$ -projective dimension of T, we give the strong notion of the $D_{C_2}$ -projective global dimension of B. Set: $S{D}_{C_2}\text{-}PD\left(B\right)=\sup \left\{D_{C_2}\text{-}p{d}_B\left(U{\otimes }_{A}D\right)|D\in D_{C_1}P\left(A\right)\right\}$ .

Theorem 4.2. Assume that ${}_A{C}_1$ and ${}_B{C}_2$ are semidualizing. Let $C=p\left(C_1\mathrm{,}{C}_2\right)$ and U Ding C-compatible. If $M={\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}$ be a left T-module and $S{D}_{C_2}\text{-}PD\left(B\right)<\infty$ , then:

$\begin{array}{l}\max \left\{D_{C_1}\text{-}pd\left(M_1\right),\left(D_{C_2}\text{-}pd\left(M_2\right)-S{D}_{C_2}\text{-}PD\left(B\right)\right)\right\}\le D_C\text{-}pd\left(M\right)\\ \le \max \left\{\left(D_{C_1}\text{-}pd\left(M_1\right)\right)+\left(S{D}_{C_2}\text{-}PD\left(B\right)\right)+1,D_{C_2}\text{-}pd\left(M_2\right)\right\}.\end{array}$

Proof. Let $k\mathrm{<mo>\; :\; </mo>}=S{D}_{C_2}\text{-}PD\left(B\right)$ . Firstly, we prove that

$\max \left\{D_{C_1}\text{-}pd\left(M_1\right),\left(D_{C_2}\text{-}pd\left(M_2\right)-k\right)\right\}\le D_C\text{-}pd\left(M\right)$ .

We may assume that $n:=D_C\text{-}pd\left(M\right)<\infty$ . Then there is an exact sequence

$0\to D^n\to \cdots \to D^1\to D^0\to M\to 0$

with $D^i={\left(\begin{array}{c}{D}_1^i\\ D_2^i\end{array}\right)}_{{\phi }^{D^i}}\in D_{C}P\left(T\right)$ . Thus we achieve an exact sequence.

$0\to D_1^n\to D_1^{n-1}\to \cdots \to D_1^0\to M_1\to 0$

with $D_1^i\in D_{C_1}P\left(A\right)$ by Theorem 3.5. Thus, $D_{C_1}\text{-}pd\left(M_1\right)\le n$ .

Furthermore, according to Theorem 3.5, there is an exact sequence in B-Mod for each i

$0\to U{\otimes }_A{D}_1^i\to D_2^i\to \overline{D_2^i}\to 0$

with $\overline{D_2^i}\in D_{C_2}P\left(B\right)$ . Then $D_{C_2}\text{-}pd\left(D_2^i\right)=D_{C_2}\text{-}pd\left(U{\otimes }_A{D}_1^i\right)\le k$ by [ [14] , Theorem 3.2]. There exists an exact sequence in B-Mod:

$0\to D_2^n\to D_2^{n-1}\to \cdots \to D_2^0\to M_2\to 0.$

By [ [14] , Theorem 3.2], $D_{C_2}\text{-}pd\left(M_2\right)\le n+k$ .

Next, we prove that $D_C\text{-}pd\left(M\right)\le \max \left\{\left(D_{C_1}\text{-}pd\left(M_1\right)\right)+k+1,D_{C_2}\text{-}pd\left(M_2\right)\right\}$ . We may assume that: $m:=\max \left\{\left(D_{C_1}\text{-}pd\left(M_1\right)\right)+k+1,D_{C_2}\text{-}pd\left(M_2\right)\right\}<\infty$ , $n_1:=D_{C_1}\text{-}pd\left(M_1\right)<\infty$ and $n_2:=D_{C_2}\text{-}pd\left(M_2\right)<\infty$ . Since $D_{C_1}\text{-}pd\left(M_1\right)=n_1\le m-k-1$ , we have an exact sequence in A-Mod:

$0\to D_1^{m-k-1}\to \cdots \to D_1^{n_2-k}\to \cdots \stackrel{f_1^1}{\to }{D}_1^0\stackrel{f_1^0}{\to }{M}_1\to 0$

with $D_1^i\in D_{C_1}P\left(A\right)$ . There exists an epimorphism $D_2^0\stackrel{g_2^0}{\to }{M}_2\to 0$ with $D_2^0\in D_{C_2}P\left(B\right)$ by [ [12] , Proposition 1.8]. Let $K_1^i=\ker f_1^i$ and define the map $f_2^0\mathrm{<mo>\; :\; </mo>}U{\otimes }_A{D}_1^0\oplus D_2^0$ to be $\left({\phi }^M\left(1_u\otimes f_1^0\right)\right)\oplus g_2^0$ . Then we get an exact sequence

$0\to {\left(\begin{array}{c}{K}_1^1\\ K_2^1\end{array}\right)}_{{\phi }^{K^1}}\to \left(\begin{array}{c}{D}_1^0\\ \left(U{\otimes }_A{D}_1^0\right)\oplus D_2^0\end{array}\right)\stackrel{\left(\begin{array}{c}{f}_1^0\\ f_2^0\end{array}\right)}{\to }M\to 0.$

In a similar way, there exists an exact sequence of B-modules $D_2^1\stackrel{g_2^1}{\to }{K}_2^1\to 0$ with $D_2^1\in D_{C_2}P\left(B\right)$ . So we obtain an exact sequence

$0\to {\left(\begin{array}{c}{K}_1^2\\ K_2^2\end{array}\right)}_{{\phi }^{K^2}}\to \left(\begin{array}{c}{D}_1^1\\ \left(U{\otimes }_A{D}_1^1\right)\oplus D_2^1\end{array}\right)\to {\left(\begin{array}{c}{K}_1^1\\ K_2^1\end{array}\right)}_{{\phi }^{K^1}}\to 0.$

Repeating this process, we obtain an exact sequence

$\begin{array}{l}0\to \left(\begin{array}{c}0\\ K_2^{m-k}\end{array}\right)\to \left(\begin{array}{c}{D}_1^{m-k-1}\\ \left(U{\otimes }_A{D}_1^{m-k-1}\right)\oplus D_2^{m-k-1}\end{array}\right)\stackrel{\left(\begin{array}{c}{f}_1^{m-k-1}\\ f_2^{m-k-1}\end{array}\right)}{\to }\cdots \\ \to \left(\begin{array}{c}{D}_1^1\\ \left(U{\otimes }_A{D}_1^1\right)\oplus D_2^1\end{array}\right)\stackrel{\left(\begin{array}{c}{f}_1^1\\ f_2^1\end{array}\right)}{\to }\left(\begin{array}{c}{D}_1^0\\ \left(U{\otimes }_A{D}_1^0\right)\oplus D_2^0\end{array}\right)\stackrel{\left(\begin{array}{c}{f}_1^0\\ f_2^0\end{array}\right)}{\to }\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)\to 0.\end{array}$

Note that $D_{C_2}\text{-}pd\left(\left(U{\otimes }_A{D}_1^i\right)\oplus D_2^i\right)=D_{C_2}\text{-}pd\left(U{\otimes }_A{D}_1^i\right)\le k$ , $i\in \left\{\mathrm{0,}\cdots \mathrm{,}m-k-1\right\}$ . By [ [14] , Theorem 3.2], the exact sequence $0\to K_2^{m-k}\to$ $\left(U{\otimes }_A{D}_1^{m-k-1}\right)\oplus D_2^{m-k-1}\to \cdots \to \left(U{\otimes }_A{D}_1^1\right)\oplus D_2^1\to \left(U{\otimes }_A{D}_1^0\right)\oplus G_2^0\to M_2\to 0$ gives that $D_{C_2}\text{-}pd\left(K_2^{m-k}\right)\le \max \left\{k,n_2-m+k\right\}=k$ . As a result, we have an exact sequence in B-Mod

$0\to D_2^m\to \cdots \to D_2^{m-k+1}\to D_2^{m-k}\to K_2^{m-k}\to \mathrm{0,}$

which induces an exact sequence in T-Mod:

$\begin{array}{l}0\to \left(\begin{array}{c}0\\ D_2^m\end{array}\right)\to \cdots \to \left(\begin{array}{c}0\\ D_2^{m-k+1}\end{array}\right)\to \left(\begin{array}{c}0\\ D_2^{m-k}\end{array}\right)\\ \to \left(\begin{array}{c}{D}_1^{m-k-1}\\ \left(U{\otimes }_A{D}_1^{m-k-1}\right)\oplus D_2^{m-k-1}\end{array}\right)\stackrel{\left(\begin{array}{c}{f}_1^{m-k-1}\\ f_2^{m-k-1}\end{array}\right)}{\to }\cdots \\ \to \left(\begin{array}{c}{D}_1^1\\ \left(U{\otimes }_A{D}_1^1\right)\oplus D_2^1\end{array}\right)\stackrel{\left(\begin{array}{c}{f}_1^1\\ f_2^1\end{array}\right)}{\to }\left(\begin{array}{c}{D}_1^0\\ \left(U{\otimes }_A{D}_1^0\right)\oplus D_2^0\end{array}\right)\stackrel{\left(\begin{array}{c}{f}_1^0\\ f_2^0\end{array}\right)}{\to }\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)\to 0.\end{array}$

Since all $\left(\begin{array}{c}{D}_1^i\\ \left(U{\otimes }_A{D}_1^0\right)\oplus D_2^i\end{array}\right)$ and $\left(\begin{array}{c}0\\ D_2^j\end{array}\right)$ are $D_C$ -projective by Theorem 3.5, $D_C\text{-}pd\left(M\right)\le m$ .¨

Corollary 4.3. Assume that ${}_A{C}_1$ and ${}_B{C}_2$ are semidualizing. Let $C=p\left(C_1\mathrm{,}{C}_2\right)$ and U Ding C-compatible. If $S{D}_{C_2}\text{-}PD\left(B\right)<\infty$ , then $D_C\text{-}pd\left(M\right)<\infty$ if and only if $D_{C_1}\text{-}pd\left(M_1\right)<\infty$ and $D_{C_2}\text{-}pd\left(M_2\right)<\infty$ .

Theorem 4.4. Assume that ${}_A{C}_1$ and ${}_B{C}_2$ are semidualizing. Let $C=p\left(C_1\mathrm{,}{C}_2\right)$ and U Ding C-compatible. Then

$\begin{array}{l}\max \left\{D_{C_1}\text{-}PD\left(A\right),D_{C_2}\text{-}PD\left(B\right)\right\}\le D_C\text{-}PD\left(T\right)\\ \le \max \left\{D_{C_1}\text{-}PD\left(A\right)+S{D}_{C_2}\text{-}PD\left(B\right)+1,D_{C_2}\text{-}PD\left(B\right)\right\}.\end{array}$

Proof. Firstly, we show that the left side of the inequality. Assume that $n:=D_C\text{-}PD\left(T\right)<\infty$ . Let $M_1\in A\text{-Mod}$ and $M_2\in B\text{-Mod}$ . Because $D_C\text{-}pd\left(\left(\begin{array}{c}{M}_1\\ U{\otimes }_A{M}_1\end{array}\right)\right)\le n$ and $D_C\text{-}pd\left(\left(\begin{array}{c}0\\ M_2\end{array}\right)\right)\le n$ , $D_{C_1}\text{-}pd\left(M_1\right)\le n$ and $D_{C_2}\text{-}pd\left(M_2\right)\le n$ by Lemma 4.1. Consequently, $D_{C_1}\text{-}PD\left(A\right)\le n$ and $D_{C_2}\text{-}PD\left(B\right)\le n$ .

Secondly, we show that the right side of the inequality. Assume that:

$m:=\max \left\{D_{C_1}\text{-}PD\left(A\right)+S{D}_{C_2}\text{-}PD\left(B\right)+1,D_{C_2}\text{-}PD\left(B\right)\right\}<\infty$ .

Then $D_{C_1}\text{-}PD\left(A\right)<\infty$ and $S{D}_{C_2}\text{-}PD\left(B\right)\le D_{C_2}\text{-}PD\left(B\right)<\infty$ . Let $M={\left(\begin{array}{c}{M}_1\\ M_2\end{array}\right)}_{{\phi }^M}$ be a left T-module. According to Theorem 4.2, $D_C\text{-}pd\left(M\right)\le \max \left\{D_{C_1}\text{-}PD\left(A\right)+S{D}_{C_2}\text{-}PD\left(B\right)+1,D_{C_2}\text{-}PD\left(B\right)\right\}$ .

Corollary 4.5. Assume that ${}_A{C}_1$ and ${}_B{C}_2$ are semidualizing. Let $C=p\left(C_1\mathrm{,}{C}_2\right)$ and U Ding C-compatible. Then $D_C\text{-}PD\left(T\right)<\infty$ if and only if $D_{C_1}\text{-}PD\left(A\right)<\infty$ and $D_{C_2}\text{-}PD\left(B\right)<\infty$ .

Corollary 4.6. Assume that ${}_R{C}_1$ is semidualizing. Let $T\left(R\right)=\left(\begin{array}{cc}R& 0\\ R& R\end{array}\right)$ and $C=p\left(C_1\mathrm{,}{C}_2\right)$ . Then $D_C\text{-}PD\left(T\left(R\right)\right)=D_{C_1}\text{-}PD\left(R\right)+1$ .

Proof. We know that R is Ding C-compatible and $S{D}_{C_1}\text{-}PD\left(R\right)=0$ . Therefore by Theorem 4.4,

$D_{C_1}\text{-}PD\left(R\right)\le D_C\text{-}PD\left(T\left(R\right)\right)\le D_{C_1}\text{-}PD\left(R\right)+1$ .

It is obvious in the case $D_{C_1}\text{-}PD\left(R\right)=\infty$ . We may assume that $n:=D_{C_1}\text{-}PD\left(R\right)<\infty$ . Then there exists a left R-module M with $D_{C_1}\text{-}pd\left(M\right)=n$ and ${\text{Ext}}_R^n\left(M\mathrm{,}X\right)\ne 0$ for some $X\in {\mathcal{F}}_{C_1}\left(R\right)$ by [ [12] , Theorem 2.4]. Now we consider an exact sequence in $T\left(R\right)$ -Mod:

$0\to \left(\begin{array}{c}0\\ M\end{array}\right)\to {\left(\begin{array}{c}M\\ M\end{array}\right)}_{1_M}\to \left(\begin{array}{c}M\\ 0\end{array}\right)\to 0.$

By applying the long exact sequence theorem to the preceding exact sequence, we obtain that

$\begin{array}{l}\cdots \to {\text{Ext}}_{T\left(R\right)}^n\left(\left(\begin{array}{c}M\\ M\end{array}\right),\left(\begin{array}{c}0\\ X\end{array}\right)\right)\to {\text{Ext}}_{T\left(R\right)}^n\left(\left(\begin{array}{c}0\\ M\end{array}\right),\left(\begin{array}{c}0\\ X\end{array}\right)\right)\\ \to {\text{Ext}}_{T\left(R\right)}^{n+1}\left(\left(\begin{array}{c}M\\ 0\end{array}\right),\left(\begin{array}{c}0\\ X\end{array}\right)\right)\to {\text{Ext}}_{T\left(R\right)}^{n+1}\left(\left(\begin{array}{c}M\\ M\end{array}\right),\left(\begin{array}{c}0\\ X\end{array}\right)\right)\to \cdots .\end{array}$

By [ [10] , Lemma 3], we know that ${\text{Ext}}_{T\left(R\right)}^{i\ge 1}\left(\left(\begin{array}{c}M\\ M\end{array}\right)\mathrm{,}\left(\begin{array}{c}0\\ X\end{array}\right)\right)\cong {\text{Ext}}_R^{i\ge 1}\left(M\mathrm{,0}\right)=0$ .

Thus by [ [10] , Lemma 3] and the above exact sequence,

${\text{Ext}}_{T\left(R\right)}^n\left(\left(\begin{array}{c}0\\ M\end{array}\right)\mathrm{,}\left(\begin{array}{c}0\\ X\end{array}\right)\right)\cong {\text{Ext}}_{T\left(R\right)}^{n+1}\left(\left(\begin{array}{c}M\\ 0\end{array}\right)\mathrm{,}\left(\begin{array}{c}0\\ X\end{array}\right)\right)\cong {\text{Ext}}_R^n\left(M\mathrm{,}X\right)\ne 0.$

As $\left(\begin{array}{c}0\\ X\end{array}\right)\in {\mathcal{F}}_C\left(T\left(R\right)\right)$ by Corollary 2.8, we have $D_C\text{-}pd\left(\left(\begin{array}{c}M\\ 0\end{array}\right)\right)>n$ by [ [12] , Theorem 2.4]. Besides, $D_C\text{-}pd\left(\left(\begin{array}{c}M\\ 0\end{array}\right)\right)\le D_C\text{-}PD\left(T\left(R\right)\right)\le n+1$ . Thus $D_C\text{-}pd\left(\left(\begin{array}{c}M\\ 0\end{array}\right)\right)=n+1$ , which implies that $D_C\text{-}PD\left(T\left(R\right)\right)=n+1$ .¨

Acknowledgements

This research was partially supported by NSFC (Grant No. 12061026), and NSF of Guangxi Province of China (Grant No. 2020GXNSFAA159120).

The authors thank the referee for the useful suggestions.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Zhang, P. (2013) Gorenstein-Projective Modules and Symmetric Recollements. Journal of Algebra, 388, 65-80. https://doi.org/10.1016/j.jalgebra.2013.05.008
[2]	Enochs, E.E., Izurdiaga, M.C. and Torrecillas. B. (2014) Gorenstein Conditions over Triangular Matrix Rings. Journal of Pure and Applied Algebra, 218, 1544-1554. https://doi.org/10.1016/j.jpaa.2013.12.006
[3]	Mao, L.X. (2020) Gorenstein Flat Modules and Dimensions over Triangular Matrix Rings. Journal of Pure and Applied Algebra, 224, Article ID: 106207. https://doi.org/10.1016/j.jpaa.2019.106207
[4]	Mao, L.X. (2020) Cotorsion Pairs and Approximation Classes over Formal Triangular Matrix Rings. Journal of Pure and Applied Algebra, 224, Article ID: 106271. https://doi.org/10.1016/j.jpaa.2019.106271
[5]	Green, E.L. (1982) On the Representation Theory of Rings in Matrix Form. Pacific Journal of Mathematics, 100, 123-138. https://doi.org/10.2140/pjm.1982.100.123
[6]	Mao, L.X. (2022) Ding Modules and Dimensions over Formal Triangular Matrix Rings. Rendiconti Del Seminario Matematico Della Universita of Padova, 148, 1-22. https://doi.org/10.4171/RSMUP/100
[7]	Holm. H. and White. D. (2007) Foxby Equivalence over Associative Rings. Journal of Mathematics of Kyoto University, 47, 781-808. https://doi.org/10.1215/kjm/1250692289
[8]	Wakamatsu, T. (2004) Tilting Modules and Auslander’s Gorenstein Property. Journal of Algebra, 275, 3-39. https://doi.org/10.1016/j.jalgebra.2003.12.008
[9]	Bennis, D., Maaouy, R.E., Garca Rozas, J.R. and Oyonarte, L. (2022) Relative Gorenstein Flat Modules and Dimension. Communciations in Algebra, 50, 3853-3882. https://doi.org/10.1080/00927872.2022.2046765
[10]	Bennis, D., Maaouy, R.E., Garca Rozas, J.R. and Oyonarte, L. (2021) Relative Gorenstein Dimensions over Triangular Matrix Rings. Mathematics, 9, Article 2676. https://doi.org/10.3390/math9212676
[11]	Haghany, A. and Varadarajan, K. (2000) Study of Modules over Formal Triangular Matrix Rings. Journal of Pure and Applied Algebra, 147, 41-58. https://doi.org/10.1016/S0022-4049(98)00129-7
[12]	Zhang, C.X., Wang, L. and Liu, Z.K. (2014) Ding Projective Modules with Respect to a Semidualizing Module. Bulletin of the Korean Mathematical Society, 51, 339-356. https://doi.org/10.4134/BKMS.2014.51.2.339
[13]	Goodearl, K.R. and Warfield, R.B. (2004) An Introduction to Noncommutative Noetherian Rings. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511841699
[14]	Huang, Z.Y. (2022) Homological Dimensions Relative to Preresolving Subcategories II. Forum Mathematicum, 34, 507-530. https://doi.org/10.1515/forum-2021-0136