Inflation and Portfolio Management

Di Ma

Economics and Management, University of Science and Technology Beijing, China.

DOI: 10.4236/jss.2023.113022                

Abstract

Inflation effects not only the return but also the risk of the portfolio. To take the impact of inflation on portfolio into account, we propose an uncertain accurate mean-variance model with inflation. Considering the complexity of the financial and social environment, the return rate of risky assets and inflation rate are given by experts’ evaluations and treated as uncertain variables. For further discussion, we give the deterministic form of the model. Then we compare our model with a rough model that simply subtracts the inflation rate. By analyzing the difference between the results of our model and that simply subtracts the inflation rate, we show the necessity of our proposed model. After that, we provide and discuss numerical examples to illustrate the significance of the model, and conclude the paper.

Keywords

Portfolio Management, Inflation, Mean-Variance Model, Uncertain Variable

1. Introduction

Portfolio management problem is to decide how to invest in different assets in order to maximize the return of investment under the precondition of risk control. The foundation of modern portfolio theory is mean-variance model that first proposed by Markowitz (1952). After that, treating the expected return as the portfolio return, and variance as the risk has been widely accepted and expanded (Castellano & Cerqueti, 2014; Ismail & Pham, 2019). Then various models of portfolio management balancing return and risk have been proposed, such as mean-semivariance model (Markovitz, 1959), mean-absolute deviation model (Konno & Yamazaki, 1991), value-at-risk model (Jorion, 1996), mean-risk curve model (Huang, 2008), mean-semivariance-CVaR model (Najafi & Mushakhian, 2015), etc. These models have been widely used and extended (Estrada, 2007; Wei, 2018; Lux & Rüschendorf, 2019).

These researches help investors make decisions to allocate capital in different securities from different perspectives. However, when calculate the return rate and manage the risk of the investment, they use the nominal return rate. Yet, in reality, there is always inflation that makes yields different from the nominal return rate. Inflation has been concerned by scholars. Fisher effect (Fisher, 1930) was first proposed to illustrate the relationship between nominal interest rate and inflation, that is, there is a one-to-one correspondence between nominal interest rate and inflation expectation in a market with sufficient information and perfect foresight. After that, the persistence of inflation has been widely documented. Bodie (1976) believed the real return on equity is negatively related to both anticipated and unanticipated inflation. Ang et al. (2008) proposed that the real interest rate and expected inflation are two key economic variables. Fuhrer and Moore (1995) set up a standard model and implied that the persistence in the driving output process led to the persistence in inflation. Ang et al. (2007) examined alternative methods to forecast U.S. inflation and compared the effects of prediction methods.

Returns of assets are considered as random variables in the above research works, and are calculated based on the sample of historical data, which requires sufficient and valid historical data. However, when the economic environment is unstable or in some emerging markets, the historical data is invalid or missing, then if people still use probability theory and treat the returns as random variables to solve problem, it will lead to counterintuitive results (Liu, 2012). For example, unexpected events such as the outbreak of a trade war will let the historical data invalid, or people who invest in newly listed stocks may have none or no sufficient historical data, either. In order to avoid the counterintuitive results, Liu (2007) proposed uncertainty theory, using the experts’ evaluations to replace the invalid historical data. Based on this, Huang (2010) produced an uncertain portfolio theory, which systematically introduced the uncertainty theory into portfolio management. Then uncertain portfolio theory is gradually widely concerned by scholars (Qin et al., 2016; Chen et al., 2017; Li et al., 2019). So far, few researches have been done on uncertain portfolio management with inflation. This motivates us to research an uncertain portfolio management problem with inflation.

The paper proceeds as follows. We first build a new mean-variance model for portfolio management with inflation on the framework of uncertainty theory and give the deterministic equivalent form in Section 2. Then we compare our model with a rough model that simply subtracts the inflation rate in Section 3. After that, we provide and discuss numerical examples to illustrate the significance of proposed model in Section 4. Finally, we conclude the paper in Section 5.

2. Uncertain Mean-Variance Portfolio Model with Inflation

2.1. Uncertain Mean-Variance Portfolio Model

Suppose an investor is considering how to allocate all his capital to securities and risk-free asset. Let $x_i$ represent the investment proportion in the i-th security, and ${\xi }_i$ the uncertain return rate of the i-th security, $i=1,2,\cdots ,n$ , respectively. Let $x_0$ represents the investment proportion in risk-free asset, and r the rate of risk-free asset. And let $\rho$ represents the uncertain inflation rate. We assume that assets have nominal payoffs and that the investor cares about real wealth. Then the real wealth of the investment is

$y=({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}(1+{\xi }_i)+x_0(1+r))/(1+\rho )$ .

Then the real return rate of the portfolio is

$R_r=y-1=({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}(1+{\xi }_i)+x_0(1+r))/(1+\rho )-1$ .

Using expected return rate as the final return and variance as the investment risk, the optimal portfolio should be the one whose variance is not greater than the preset level and at the same time whose expected return is the maximal; or the optimal portfolio should be the one whose expected return is not less than the preset level and in the meantime whose variance is the minimal. Let a be the preset variance level the investors can tolerate. When the investor wants to purse the maximum expected return rate, the uncertain mean-variance selection model is expressed as follows:

$\{\begin{array}{l}maxE\left[({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}(1+{\xi }_i)+x_0(1+r))/(1+\rho )-1\right]\hfill \\ \text{subjectto:}\hfill \\ V\left[({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}(1+{\xi }_i)+x_0(1+r))/(1+\rho )-1\right]\le a,(I)\hfill \\ {\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}+x_0=1,\hfill \\ x_i\ge 0,i=0,1,2,\cdots ,n,\hfill \end{array}$ (1)

where E is the expected value operator of uncertain variables, and V is the variance.

2.2. Deterministic Equivalent Form

For further discussion, we give the deterministic equivalent form of the model (1) below.

Theorem 1. Suppose the i-th security return ${\xi }_i$ has regular uncertainty distribution ${\Phi }_i$ for $i=1,2,\cdots ,n$ , and inflation rate $\rho$ has regular uncertainty distributions $\Psi$ , respectively. Then the deterministic equivalent form of the model (1) is:

$\{\begin{array}{l}max({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{1+{\Phi }_i^{-1}\left(\alpha \right)}{1+{\Psi }^{-1}(1-\alpha )}d\alpha }+x_0{\displaystyle \underset{0}{\overset{1}{\int }}\frac{1+r}{1+{\Psi }^{-1}(1-\alpha )}-1})d\alpha \hfill \\ \text{subjectto:}\hfill \\ {\displaystyle \underset{0}{\overset{1}{\int }}{\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}\frac{1+{\Phi }_i^{-1}\left(\alpha \right)}{1+{\Psi }^{-1}(1-\alpha )}+x_0\frac{1+r}{1+{\Psi }^{-1}(1-\alpha )}-1-e\right)}^2}d\alpha \le a,\hfill \\ {\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}+x_0=1,\hfill \\ x_i\ge 0,i=0,1,2,\cdots ,n,\hfill \end{array}$ (2)

where

$e=({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}{\displaystyle {\int }_0^1\frac{1+{\Phi }_i^{-1}\left(\alpha \right)}{1+{\Psi }^{-1}(1-\alpha )}d\alpha }+x_0{\displaystyle {\int }_0^1\frac{1+r}{1+{\Psi }^{-1}(1-\alpha )}}-1)d\alpha .$

Proof: Since inflation rate $\rho$ is positive, and the i-th security return ${\xi }_i$ cannot be lower than −1 for $i=0,1,2,\cdots ,n$ , y is strictly increasing with respect to ${\xi }_i$ and decreasing with respect to $\rho$ . From the operational law of the uncertainty theorem (Liu, 2012), the inverse uncertainty distribution of

$R_r=y-1=({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}(1+{\xi }_i)+x_0(1+r))/(1+\rho )-1$

is

${{\rm Y}}^{-1}(\alpha )=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}\left(1+{\Phi }_i^{-1}\left(\alpha \right)\right)+x_0\left(1+r\right)}{1+{\Psi }^{-1}(1-\alpha )}-1,\alpha \in (0,1).$

Then according to the equations of expected value and variance of uncertain variables, the objective function of the model (1) is equivalent to

$E[y]=({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}{\displaystyle {\int }_0^1\frac{1+{\Phi }_i^{-1}\left(\alpha \right)}{1+{\Psi }^{-1}(1-\alpha )}d\alpha }+x_0{\displaystyle {\int }_0^1\frac{1+r}{1+{\Psi }^{-1}(1-\alpha )}-1)}d\alpha ,$

and we have

$V[y]={\displaystyle {\int }_0^1{\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}\frac{1+{\Phi }_i^{-1}\left(\alpha \right)}{1+{\Psi }^{-1}(1-\alpha )}+x_0\frac{1+r}{1+{\Psi }^{-1}(1-\alpha )}-1-e\right)}^2}d\alpha ,$

where

$e=({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}{\displaystyle {\int }_0^1\frac{1+{\Phi }_i^{-1}\left(\alpha \right)}{1+{\Psi }^{-1}(1-\alpha )}d\alpha }+x_0{\displaystyle {\int }_0^1\frac{1+r}{1+{\Psi }^{-1}(1-\alpha )}}-1)d\alpha .$

Thus, the theorem is verified.

3. Comparison with the Model That Subtracts the Inflation Rate

For some studies (e.g., Bodie, 1976; Fama, 1981), the researchers use $1+R_n-\rho$ represents the real wealth of portfolio, where $R_n$ is the nominal return rate of portfolio and $\rho$ is the uncertain inflation rate. Since the initial formula is

$1+R_n=(1+R_r)(1+\rho )=1+R_r+\rho +R_r\times \rho ,$

where $R_r$ is the real return rate, the term $R_r\times \rho$ is so small for small values of $R_r$ and $\rho$ that some researchers ignore it. However, the return rates of securities such as stock and futures sometimes can be high, when the inflation rate exists and is not too small, the term $R_r\times \rho$ cannot be ignored. So we compare the difference of the results of our model and that simply subtracts the inflation rate by computing the optimal real wealth and real return rate.

3.1. Mean-Variance Model That Subtracts the Inflation Rate

Under the same conditions, when use

$1+R_n-\rho ={\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}\left(1+{\xi }_i\right)+x_0(1+r)-\rho$

represents the real wealth of portfolio and use

$R_n-\rho ={\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}\left(1+{\xi }_i\right)+x_0(1+r)-\rho -1$

represents the real return rate of portfolio, the uncertain mean-variance portfolio model is expressed as follows:

$\{\begin{array}{l}maxE\left[{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}\left(1+{\xi }_i\right)+x_0(1+r)-1-\rho \right]\hfill \\ \text{subjectto:}\hfill \\ V\left[{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}(1+{\xi }_i)+x_0(1+r)-1-\rho \right]\le a,(I)\hfill \\ {\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}+x_0=1,\hfill \\ x_i\ge 0,i=0,1,2,\cdots ,n,\hfill \end{array}$ (3)

where E is the expected value operator of uncertain variables, and V is the variance.

3.2. Comparison with the Model

Next, we will analyze whether the rough model (3) can get the optimal solution of the model (1).

Theorem 2. The optimal portfolio of model (3) either exceeds the risk tolerance, or gets the return that lower than the optimal return of the model (1).

Proof: Let $X=(x_1,x_2,\cdots ,x_n,x_0)$ . The condition (I) in the models (1) and (3) be denoted as $g_1(X)\le a$ and $g_2(X)\le a$ , respectively. Suppose $X_1^{*}$ is an optimal solution of the model (1) and $X_2^{*}$ is an optimal solution of the model (3). Let $f_1(\cdot )$ denotes the objective function of the model (1) and $f_2(\cdot )$ the objective function of the model (3).

1) When $X_2^{*}$ is a feasible solution of the model (1), we have $f_1(X_2^{*})\le f_1(X_1^{*})$ .

2) When $X_2^{*}$ is not a feasible solution of the model (1), that is, $g_1(X_2^{*})>a$ , $X_2^{*}$ exceeds the constraint (I) in the model (1).

Obviously, the optimal solution of model (3) either exceeds the risk control constraint, or gets the objective return rate that lower than the optimal return rate of the model (1). Thus, the theorem is verified.

4. Numerical Examples

To illustrate the significance of the proposed uncertain portfolio management model, this section will give numerical examples.

4.1. The Results of Uncertain Mean-Variance Model

Suppose an investor wants to select portfolio from ten securities and a risk-free asset, and gets the experts’ estimations on the candidate securities’ return rates. The uncertainty distributions of the ten security returns are obtained and given in Table 1.

Suppose the return rate of risk-free asset r is 0.02. The experts believe that the inflation rate has uncertainty distribution.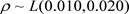

Assume the investor adopts the mean-variance selection principle and wants to pursue the maximum expected return with the maximum tolerable variance at 0.002. By using MATLAB2016, the optimal portfolio is obtained and provided in Table 2. The investor should choose the third security and risk-free asset, and the proportions are 56.4% and 43.6%, respectively. The optimal expected real return is 6.06%. And when the mean and volatility of inflation rate change, the allocation of money to 10 securities and risk-free asset change accordingly. That is, the results in Table 2 are not the optimal solution anymore.

4.2. Comparison with the Model Subtracting the Inflation Rate

As mentioned in the Section 3, some studies subtract the inflation rate for simplicity of calculation. Based on numerical examples, we compare the difference of the results of our model and the way that subtracts the inflation rate.

Same as examples in Section 4.1, the uncertainty distributions of the ten security returns are given in Table 1 and the risk-free asset return r is 0.02. And the maximum tolerable variance $a=0.002$ . The optimal portfolio is obtained and provided in Table 3.

And the optimal expected real return is 5.97%. Obviously, the optimal return of the model that subtracting the inflation rate is no better than the accurate model we propose. We also change the mean of inflation rate to do the experiment. The results show that if the investor uses the model that subtracts the inflation rate, he won’t change his investment proportion when the mean of inflation rate changes.

And we adjust the maximum tolerable variance a to get the efficient frontier of portfolio of the two different models, which is shown in Figure 1. We can see that there is a difference between the expected return rate of the two models no matter how a is. The results obtained by using simplified model cannot be close enough to the accurate model that we propose in Section 2.

Table 1. Linear uncertain return rates of 10 securities.

Figure 1. Efficient frontier of portfolios of accurate model and the model subtracting inflation rate.

Table 2. Allocation of money to 10 securities and risk-free asset when $a=0.002$ .

Table 3. Allocation of money to 10 securities and risk-free asset when $a=0.002$ of the model subtracting the inflation rate.

5. Conclusion

In reality inflation has great effect on investment. And there exists the situation where the returns of risky asset and inflation rate cannot be effectively measured by past data due to unexpected events and complexity of financial and social environment and have to be evaluated by experts. In this paper, we propose a new uncertain portfolio management model with consideration of inflation based on framework of uncertainty theory. We give the deterministic forms of the model and compare our model with a rough model that simply subtracts the inflation rate, and infer that the optimal solution of rough model either exceeds the risk tolerance, or gets the return which is lower than the optimal return of the model we proposed.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Ang, A., Bekaert, G., & Wei, M. (2007). Do Macro Variables, Asset Markets, or Surveys Forecast Inflation Better? Journal of Monetary Economics, 54, 1163-1212. https://doi.org/10.1016/j.jmoneco.2006.04.006
[2]	Ang, A., Bekaert, G., & Wei, M. (2008). The Term Structure of Real Rates and Expected Inflation. The Journal of Finance, 63, 797-849. https://doi.org/10.1111/j.1540-6261.2008.01332.x
[3]	Bodie, Z. (1976). Common Stocks as a Hedge against Inflation. The Journal of Finance, 31, 459-470. https://doi.org/10.1111/j.1540-6261.1976.tb01899.x
[4]	Castellano, R., & Cerqueti, R. (2014). Mean-Variance Portfolio Selection in Presence of Infrequently Traded Stocks. European Journal of Operational Research, 234, 442-449. https://doi.org/10.1016/j.ejor.2013.04.024
[5]	Chen, L., Peng, J., Zhang, B., & Rosyida, I. (2017). Diversified Models for Portfolio Selection Based on Uncertain Semivariance. International Journal of Systems Science, 48, 637-648. https://doi.org/10.1080/00207721.2016.1206985
[6]	Estrada, J. (2007). Mean-Semivariance Behavior: Downside Risk and Capital Asset Pricing. International Review of Economics & Finance, 16, 169-185. https://doi.org/10.1016/j.iref.2005.03.003
[7]	Fama, E. F. (1981). Stock Returns, Real Activity, Inflation, and Money. The American Economic Review, 71, 545-565.
[8]	Fisher, I. (1930). Theory of Interest: As Determined by Impatience to Spend Income and Opportunity to Invest It. Augustusm Kelly Publishers.
[9]	Fuhrer, J., & Moore, G. (1995). Inflation Persistence. The Quarterly Journal of Economics, 110, 127-159. https://doi.org/10.2307/2118513
[10]	Huang, X. (2008). Portfolio Selection with a New Definition of Risk. European Journal of Operational Research, 186, 351-357. https://doi.org/10.1016/j.ejor.2007.01.045
[11]	Huang, X. (2010). Portfolio Analysis: From Probabilistic to Credibilistic and Uncertain Approaches. Springer-Verlag.
[12]	Ismail, A., & Pham, H. (2019). Robust Markowitz Mean-Variance Portfolio Selection Under Ambiguous Covariance Matrix. Mathematical Finance, 29, 174-207. https://doi.org/10.1111/mafi.12169
[13]	Jorion, P. (1996). Risk2: Measuring the Risk in Value at Risk. Financial Analysts Journal, 52, 47-56. https://doi.org/10.2469/faj.v52.n6.2039
[14]	Konno, H., & Yamazaki, H. (1991). Mean-Absolute Deviation Portfolio Optimization Model and Its Applications to Tokyo Stock Market. Management Science, 37, 519-531. https://doi.org/10.1287/mnsc.37.5.519
[15]	Li, B., Sun, Y., Aw, G., & Teo, K. L. (2019). Uncertain Portfolio Optimization Problem under a Minimax Risk Measure. Applied Mathematical Modelling, 76, 274-281. https://doi.org/10.1016/j.apm.2019.06.019
[16]	Liu, B. (2007). Uncertainty Theory (2nd ed.). Springer-Verlag.
[17]	Liu, B. (2012). Why Is There a Need for Uncertainty Theory. Journal of Uncertain Systems, 6, 3-10.
[18]	Lux, T., & Rüschendorf, L. (2019). Value-at-Risk Bounds with Two-Sided Dependence Information. Mathematical Finance, 29, 967-1000. https://doi.org/10.1111/mafi.12192
[19]	Markovitz, H. (1959). Portfolio Selection: Efficient Diversification of Investments. John Wiley.
[20]	Markowitz, H. (1952). Portfolio Selection. The Journal of Finance, 7, 77-91. https://doi.org/10.1111/j.1540-6261.1952.tb01525.x
[21]	Najafi, A. A., & Mushakhian, S. (2015). Multi-Stage Stochastic Mean-Semivariance-Cvar Portfolio Optimization under Transaction Costs. Applied Mathematics and Computation, 256, 445-458. https://doi.org/10.1016/j.amc.2015.01.050
[22]	Qin, Z., Kar, S., & Zheng, H. (2016). Uncertain Portfolio Adjusting Model Using Semiabsolute Deviation. Soft Computing, 20, 717-725. https://doi.org/10.1007/s00500-014-1535-y
[23]	Wei, P. (2018). Risk Management with Weighted Var. Mathematical Finance, 28, 1020-1060. https://doi.org/10.1111/mafi.12160