Development of a Quantitative Prediction Support System Using the Linear Regression Method

Jeremie Ndikumagenge, Vercus Ntirandekura

Center of Research in Infrastructure, Environment and Technology (CRIET), University of Burundi, Bujumbura, Burundi.

DOI: 10.4236/jamp.2023.112024                

Abstract

The development of prediction supports is a critical step in information systems engineering in this era defined by the knowledge economy, the hub of which is big data. Currently, the lack of a predictive model, whether qualitative or quantitative, depending on a company’s areas of intervention can handicap or weaken its competitive capacities, endangering its survival. In terms of quantitative prediction, depending on the efficacy criteria, a variety of methods and/or tools are available. The multiple linear regression method is one of the methods used for this purpose. A linear regression model is a regression model of an explained variable on one or more explanatory variables in which the function that links the explanatory variables to the explained variable has linear parameters. The purpose of this work is to demonstrate how to use multiple linear regressions, which is one aspect of decisional mathematics. The use of multiple linear regressions on random data, which can be replaced by real data collected by or from organizations, provides decision makers with reliable data knowledge. As a result, machine learning methods can provide decision makers with relevant and trustworthy data. The main goal of this article is therefore to define the objective function on which the influencing factors for its optimization will be defined using the linear regression method.

Keywords

Prediction, Linear Regression, Machine Learning, Least Squares Method

1. Introduction

In this digital age, improving a system’s yields is accomplished by rationalizing the mobilized resources involved in a production process through the use of optimization methods and models. To accomplish this, specialists in various fields such as political economists, statisticians, actuaries, mathematicians, and others can make significant contributions to solving certain optimization challenges such us climate factors in agriculture harvesting. Proven optimization methods can be used for this purpose.

The emergence of new data concepts such as big data or voluminous and numerous data necessitates the development of new tools, as evidenced by the rise of optimization or/and classification. Multiple linear regression models, particularly parametric models, are frequently used in data analysis procedures. The linear regression model has a wide range of applications [1] . It enables us to perform analyses and make predictions in particular. As a result, if there is a strict linear relationship between the variable to be explained or target variable and the explanatory variable or predictive variable, the prediction of the value for the target variable is unequivocal when the value for the explanatory variable is known. The model’s random error term is ignored, and the magnitude of this error provides the accuracy of the established estimation [2] .

In order to achieve the main goal, the present work will employ linear regression and the least squares method as mathematical tools and equipment. Furthermore, Python language utilities will be solicited for parameter value determination before discussing the obtained results and emphasizing their novelty and potential implications.

2. Materials, Tools, Equipment and Methods

2.1. Material

The spreadsheet and Python language allow you to create a linear regression model and determine the values of the model’s parameters by solving the system obtained by using the least squares method.

2.2. Tools and Equipment

Sums are calculated in Excel, while python language libraries like numpy help with numerical calculations when pandas are used during the model data loading process.

2.3. Methods

When applied to the linear regression model, the least squares method yields exact and correct results. The least squares method is a tool used in all observational sciences for error theory or purely algebraic estimation [3] . It solves the linear regression model equation by determining the values of the parameters. According to [the Gauss-Markov theorem], “for a linear model, if the errors are uncorrelated and have zero expectation together with variances equal, then the least squares estimator is the best linear unbiased estimator of the coefficients” [4] .

In this present work, the least squares method is used in this work to define the objective function of the model, from which a system of equations is derived by calculating the partial derivatives with respect to the model’s coefficients.

2.3.1. Mathematical Modeling

Linear regression models are classified into two types: 1) simple linear regression, which employs the traditional intercept slope form and requires a and b to be learned in order to make accurate predictions; and 2) multiple linear regression, which begins with the estimation of parameters involving an endogenous variable y and p number of exogenous variables $x_j$ .

2.3.2. Model of Linear Regression

The equations x and y represent the simple linear regression equation and the multiple linear regression equation, respectively.

$y=ax+b$ (1)

$Y_i=a_0+a_1{x}_{i,1}+a_2{x}_{i,2}+a_3{x}_{i,3}+\cdots +a_p{x}_{i,p}+{\epsilon }_i$ (2)

where Y_i is the i-th observation of variable y; $x_{i,j}$ is the i-th observation of variable j-th variable; ${\epsilon }_i$ is the model’s error. It summarizes the missing information that would allow the values of y to be explained linearly using the p variables $x_j$ .

To solve the regression problem, we must estimate p + 1 parameters, which leads to the equation number (3) Written as a matrix.

$Y=Xa+\epsilon$ (3)

The dimensions of the matrices involved in the expression of equation 3 are as follows: for Y, its dimension is (n, 1), for X, it is (n, p + 1), for a, it is (p + 1, 1), and finally for its dimension is (n, 1).

The (n, p + 1)-dimensional matrix X contains all of the observations on the exogens, with the first column formed by the value 1 indicating the integration of the constant a₀ in the model equation.

$\left(\begin{array}{cccc}1& x_{1,1}& \cdots & x_{1,p}\\ 1& x_{2,1}& \cdots & x_{2,p}\\ 1& x_{n,1}& \cdots & x_{n,p}\end{array}\right)$

2.3.3. Prediction Using Linear Regression

The linear regression model is used in prediction because of three key elements. The model data (dataset) contains the questions x and answers y for the problem to be solved. This data is used to generate a model represented by a mathematical function, with the coefficients of this function serving as the model’s parameters. The cost function or objective function is the set of errors in the model on the data.

3. Results and Discussion

In the next article we plan to carry out tests of the designed support on climatic data in order to predict the harvestable quantities according to the influencing climatic factors. Thus, for practical reasons, the model data (dataset) used to determine the objective function will be taken from those provided by the Geographical Institute of Burundi (IGEEBU) in 2018.

3.1. Production Estimation Based on Weather Conditions

In this study, we used test data from a sampling provided by the Geographical Institute of Burundi as shown on Table 1.

The parameters a, b, c, d, e, f, g, h, i, j, and k are determined by applying the least squares method to the model, which is a formulated linear function.

$f\left(x_i\right)=a{x}_1+b{x}_2+c{x}_3+d{x}_4+e{x}_5+f{x}_6+g{x}_7+h{x}_8+i{x}_9+j{x}_{10}+k$ (4)

To begin, let’s use the least squares method on the model’s linear function:

$J\left(a,b,c,d,e,f,g,h,i,j\right)=\frac{1}{2m}{\displaystyle {\sum }_{i=0}^m{\left(f\left(x_i\right)-y^{\left(i\right)}\right)}^2}$ (5)

$\begin{array}{l}J\left(a,b,c,d,e,f,g,h,i,j\right)\\ =\frac{1}{2m}{\displaystyle {\sum }_{i=0}^m{\left(a{x}_1+b{x}_2+c{x}_3+d{x}_4+e{x}_5+f{x}_6+g{x}_7+h{x}_8+i{x}_9+j{x}_{10}+k-y^{\left(i\right)}\right)}^2}\end{array}$ (6)

Calculating the partial derivatives in relation to the linear function coefficients yields the equations as shown on Table 2.

We can deduce the system of equations from these partial derivatives calculated with respect (7).

3.1.1. Resultant 1: Gradient Descent Equation System

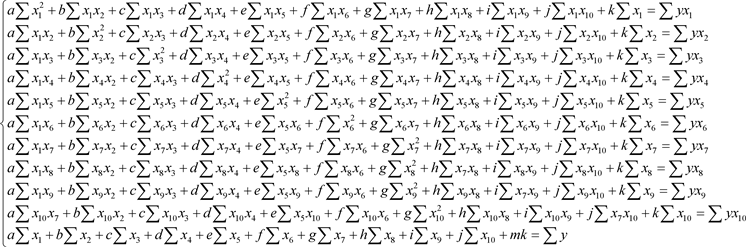(7)

The system of Equations (7) is shown in matrix form in system (8) below:

(8)

Table 1. Dataset.

X₁: The solar radiation Level, X₂: Water stress level, X₃: Temperature of the air, X₄: Soil depth, X₅: Temperature of the soil, X₆: Evaporation rate, X₇: Precipitation quantity, X₈: Wind speed, X₉: Soil Humidity, X₁₀: represents relative air Humidity, and Y: represents Production.

Table 2. Least square calculation.

3.1.2. Resultat 2: Factor Values or Climate Parameters

The application of the least squares method to the model’s test data yields the effective values of the model’s parameters as shown by the system results (9)

$\left[\begin{array}{ccccccccccc}426.652529& 357.07572& 693.95105& 700.2115& 569.2397& 290.040825& 1358.78317& 288.0637& 1326.553275& 438.8171& 46.423\\ 357.07572& 407.1607& 734.049& 670.9864& 446.985& 246.5568& 1090.7306& 171.9635& 1103.03617& 325.8305& 38.75\\ 693.95105& 734.049& 1421.6475& 1600.525& 929.551& 456.20575& 2249.8145& 392.0955& 2312.8455& 683.094& 78.95\\ 700.2115& 670.9864& 1600.525& 2782.2836& 1123.026& 381.6267& 2855.913& 558.64& 3124.10458& 903.52& 96.94\\ 569.2397& 446.985& 929.551& 1123.026& 855.6154& 372.411325& 1859.8063& 421.74725& 1854.215265& 623.71105& 64.17\\ 290.040825& 246.5568& 456.20575& 381.6267& 372.411325& 203.687225& 883.32075& 184.1644& 846.836535& 283.8375& 30.275\\ 1358.78317& 1090.7306& 2249.8145& 2855.913& 1859.8063& 883.32075& 5902.4975& 1258.4885& 60058.9759& 2078.836& 185.71\\ 288.0637& 171.9635& 392.0955& 558.64& 421.74725& 184.1644& 1258.4885& 305.7966& 1265.3106& 461.1333& 39.24\\ 1326.553275& 1103.03617& 2312.8455& 3124.10458& 1854.215265& 846.836535& 60058.9759& 1265.3106& 6319.269074& 2142.18105& 189.472\\ 438.8171& 325.8305& 683.094& 903.52& 623.71105& 283.8375& 2078.836& 461.1333& 2142.18105& 763.7708& 64\\ 46.423& 38.75& 78.95& 96.94& 64.17& 30.275& 185.71& 39.24& 189.472& 64& 6\end{array}\right]\ast \left[\begin{array}{c}a\\ b\\ c\\ d\\ e\\ f\\ g\\ h\\ i\\ j\\ k\end{array}\right]=\left[\begin{array}{c}36537.64258\\ 27742.54655\\ 60218.178\\ 81836.0083\\ 51791.8916\\ 23600.67213\\ 153136.7567\\ 32751.7518\\ 158693.3283\\ 52848.47145\\ 4380762.654\end{array}\right]$ (9)

We obtain the following values of the following parameters after solving the system (9):

$a=15022653.083623783662915$

$b=19087801.322295062243938$

$c=-19617686.517314746975898$

$d=4433188.079017613083124$

$e=-0.037048308013294$

$f=-4477342.56212795432657$

$g=293402.8806244044099$

$h=-10060668.647367989644408$

$i=-7.433182264782304$

$j=2466614.860606360249221$

$k=6.230437622139735$

The solving system (9) returns the values of the final model’s coefficients, as expressed:

$\begin{array}{l}f\left(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9\right)\\ =15022653.083x_1+19087801.322x_2-19617686.517x_3+4433188.079x_4\\ -0.037x_5-4477342.562x_6+293402.880x_7-10060668.647x_8\\ +2466614.860x_9+6.230\end{array}$

3.2. Discussion on the Obtained Results

Two results were obtained after applying the model to the study data (dataset).

1) A system of equations derived from study data using the law of the smallest squares and linear regression.

2) The values of the model’s coefficients or parameters, which can be used to minimize or maximize the differences between the final and initial models.

3) The objective function found constitutes a quantitative prediction support which can be used in various fields to estimate the values of indicators of a given process involving and interacting quantifiable and countable input factors. For the last one, at the output, the results or products obtained are themselves also quantifiable, countable and optimal according to the case.

4) The determination of the influencing factors using the gradient descent method makes it possible to minimize or maximize the objective function which ultimately can be used for prediction purposes.

A subsequent work will elucidate and investigate the avenues of application of this fourth result using case studies that trace real-world phenomena.

4. Conclusions

The objective function must be determined. Multiple linear regression allows for the determination of an objective function, which can then be optimized by adjusting the influencing factors. The precision of the influencing factors required to obtain an optimal yield has been obtained using the method of gradient descent and can be used for quantitative prediction processes or/and work.

The solution based on least squares methods coupled with multiple linear regression allowed for the determination of an objective function. The specification of influencing factors, combined with the use of gradient descent methods, transforms the latter into a tool, a support for quantitative prediction.

The use of a linear regression model, one of the artificial intelligence supervised learning methods, is what distinguishes this work from others. The work goes beyond the commonly used decision-making approaches. It focuses on prediction modeling for decision support systems in particular.

This final point will be addressed in future work. Future research will particularly concentrate on the specifications of the influencing factors of the objective function, as requested during the optimization process using the gradient descent method.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Etemadi, S. and Khashei, M. (2021) Etemadi Multiple Linear Regression. Measurement, 186, 110080. https://doi.org/10.1016/j.measurement.2021.110080
[2]	Schweppe, F.C. (1970) Power System Static-State Estimation. IEEE Transactions on Power Apparatus and Systems, 135.
[3]	Helland, I.S. (1990) Partial Least Squares Regression and Statistical Models. Scandinavian Journal of Statistics, 17, 97-114. https://www.jstor.org/stable/4616159.
[4]	Lewis, P.T. (1966) A Generalization of the Gauss-Markov Theorem. Journal of the American Statistical Association, 61, 1063-1066. https://doi.org/10.2307/2283200