1. Introduction
The initial work on the exact solution for N nonlinear internal waves governed by the nonstationary three-dimensional (3-d) Navier-Stokes equations [1] revealed an extreme sophistication of the exact solution derived with the help of experimental and theoretical programming in Maple via the Stationary Kinematic Euler-Fourier functions. To overcome this challenge, theoretical and experimental Deterministic Scalar Kinematic (DSK) structures together with theoretical and experimental Deterministic Vector Kinematic (DVK) structures have been developed in [2] to solve the Helmholtz problem for various wave systems with the help of the method of Decomposition in Invariant Structures (DIS).
Consequently, the DSK and DVK structures have been complemented by the theoretical and experimental Deterministic Scalar Dynamic (DSD) structures accompanied by the theoretical and experimental Deterministic Vector Dynamic (DVD) structures in [3] to find the exact nonstationary 3-d solution for deterministic chaos of M internal waves from J wave groups controlled by the Navier-Stokes equations. In [3], the Dirichlet problem for the Navier-Stokes equations with the help of the Helmholtz decomposition is reduced to computation of the Archimedean, Stokes, and Navier fields, whereas the kinetic energy of deterministic chaos of the exponential pulsons and oscillons turned out to be the scalar Helmholtz potential of the Navier field.
To explore properties of the kinetic energy, rectangular, diagonal, and triangular summations of the matrix of the kinetic energy and the general terms of various sums have been used in the current paper to develop quantization of the kinetic energy of deterministic chaos. Nested structures of the cumulative energy pulson, the energy pulson of propagation, the internal energy oscillon, the diagonal energy oscillon, and the external energy oscillon have been established. In turn, the energy pulsons and oscillons include the group pulsons of propagation, the internal group oscillons, the diagonal group oscillons, and the external group oscillons. Sequentially, the group pulsons and oscillons contain the wave pulsons of propagation, the internal wave oscillons, the diagonal wave oscillons, and the external wave oscillons. Consecutively, the wave pulsons and oscillons are composed of the elementary pulsons of propagation, the internal elementary oscillons, the diagonal elementary oscillons, and the external elementary oscillons.
Topology, periodicity, and integral properties of the exponential pulsons and oscillons are studied with the help of the inhomogeneous Fourier expansions via eigenfunctions in coordinates and time. This novel method allows to replace the (homogeneous) Fourier series including an unbounded number of terms with the inhomogeneous Fourier expansions containing a bounded number of terms that deliver exact solutions. Symbolic computations of the exact expansions have been performed using the experimental and theoretical programming in Maple since the functional bases include 16 inhomogeneous eigenfunctions for each variable. Results of the symbolic computations have justified by probe visualizations in x-, y-, t-directions.
The contents of this paper are following. Quantization of the kinetic energy of deterministic chaos of the exponential oscillons and pulsons is developed in Section 2, using rectangular, diagonal, and triangular summations of the matrix of the kinetic energy and the general terms of various sums. The section concludes with a summary of nested structures of energy, group, wave, elementary oscillons and pulsons.
Section 3 deals with the elementary oscillons of propagation, the elementary pulsons of propagation, the internal elementary oscillons, the diagonal elementary oscillons, and the external elementary oscillons. Eigenfunctions of the inhomogeneous Fourier expansions in x-, y-, t- are constructed in this section. The inhomogeneous Fourier expansions, periods, and averages of elementary oscillons and pulsons are computed and illustrated.
The wave oscillons of propagation, the wave pulsons of propagation, the internal wave oscillons, the diagonal wave oscillons, and the external wave oscillons are computed in Section 4 together with their periods and averages. The wave pulsons and oscillons are also displayed in the x-, y-, t-directions. In Section 5, we consider topology, periodicity, integral properties, and visualizations of the group oscillons of propagation, the group pulsons of propagation, the internal group oscillons, the diagonal group oscillons, and the external group oscillons.
In Section 6, the inhomogeneous Fourier expansions of the energy pulson of propagation, the internal energy oscillon, the diagonal energy oscillon, the external energy oscillon, and the cumulative energy pulson are developed and visualized. Section 7 contains a short discussion of main results and further developments.
2. Quantization of the Kinetic Energy
2.1. Decomposition of the Matrix of the Kinetic Energy
The kinetic energy 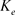 of the deterministic chaos of internal waves in a Newtonian fluid with a constant density
of the deterministic chaos of internal waves in a Newtonian fluid with a constant density 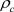 and a global velocity field
and a global velocity field  is defined by
is defined by
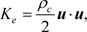 (1)
(1)
where the global velocity field is formed by velocity fields of four wave groups
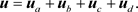 (2)
(2)
Substitution of (2) in (1) yields the kinetic energy of the deterministic chaos of the exponential oscillons and pulsons (118) of [3] in terms of the velocity fields of four wave groups
 (3)
(3)
For clarification of summation, we define a matrix of the kinetic energy  by
by
 (4)
(4)
where the braces notation 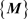 denotes the rectangular summation of all elements of the summation matrix
denotes the rectangular summation of all elements of the summation matrix 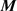 .
.
Since the velocity fields of four wave groups are expanded in the weighted experimental DVK structures  (20) of [3],
(20) of [3],
 (5)
(5)
matrix (4) takes the following form:
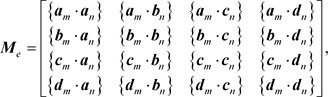 (6)
(6)
where the summation braces 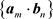 signify the rectangular summation of all elements of a summation matrix with the general term
signify the rectangular summation of all elements of a summation matrix with the general term 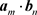 for
for 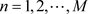 and
and 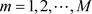 , i.e.
, i.e.
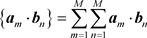 (7)
(7)
since each wave group is composed of M waves.
Primarily, we decompose ![]() as follows
as follows
![]() (8)
(8)
Here,
![]() (9)
(9)
is a diagonal matrix, which includes all diagonal elements of ![]() , and
, and
![]() (10)
(10)
is a complementary matrix, which is composed of the upper and lower triangular matrices of ![]() .
.
The kinetic energy is correspondingly decomposed as
![]() (11)
(11)
where the first sum ![]() is produced by the elements of
is produced by the elements of ![]() :
:
![]() (12)
(12)
and the second sum ![]() by the elements of
by the elements of ![]() :
:
![]() (13)
(13)
In (12)-(13), the constituents of ![]() are
are
![]() (14)
(14)
and the constituents of ![]() are
are
![]() (15)
(15)
Secondly, we expand all sums into internal sums with ![]() , which correspond to internal interaction of elementary oscillons of propagation from the
, which correspond to internal interaction of elementary oscillons of propagation from the ![]() th family, and external sums with
th family, and external sums with ![]() , which describe external interaction of elementary oscillons of propagation from the
, which describe external interaction of elementary oscillons of propagation from the ![]() th and
th and ![]() th families (see Section 2.6).
th families (see Section 2.6).
The summation matrix of the diagonal constituent ![]() of
of ![]()
![]() (16)
(16)
due to the commutative property of the dot products
![]() (17)
(17)
yields the following reduction of the rectangular summation to the diagonal and triangular summations:
![]() (18)
(18)
Similar reductions of the remaining diagonal constituents ![]() yield
yield
![]() (19)
(19)
The summation matrices of the non-diagonal constituent ![]() of
of ![]()
![]() (20)
(20)
and
![]() (21)
(21)
because of the commutative properties of the dot products:
![]() (22)
(22)
produce the following reduction of the rectangular summation to the diagonal and triangular summations:
![]() (23)
(23)
If ![]() , the asymmetric reduction (23) is converted into the symmetric reduction (18).
, the asymmetric reduction (23) is converted into the symmetric reduction (18).
Proceeding the same way for the rest of the summation matrices of the non-diagonal constituents ![]() returns
returns
![]() (24)
(24)
2.2. Wave, Group, and Energy Pulsons of Propagation
Thirdly, we define wave, group, and energy pulsons and oscillons via various combinations of dot products of the DVK structures and express the dot products in terms of the weighted experimental DSD structures (29) of [3].
General terms of the internal sums of (18)-(19) produce wave pulsons of propagation
![]() (25)
(25)
Since the DVK structures are related with the DSK structures by (20) of [3]
![]() (26)
(26)
the wave pulsons of propagation in the DSD structures take the following form:
![]() (27)
(27)
A superposition of a group of the wave pulsons of propagation
![]() (28)
(28)
is termed a group pulson of propagation ![]() . Here,
. Here, ![]() is simplified by the Pythagorean identity for the wave numbers
is simplified by the Pythagorean identity for the wave numbers
![]() (29)
(29)
Eventually, the diagonal summation of all group pulsons of propagation results in an energy pulson of propagation
![]() (30)
(30)
which shows a cumulative energy of all group pulsons of propagation.
2.3. Wave, Group, and Energy Oscillons of Diagonal External Interaction
General terms of the external sums of (18)-(19) generate wave oscillons of diagonal external interaction (diagonal wave oscillons for brevity)
![]() (31)
(31)
Using (26) and Equation (26) with ![]() , we obtain the diagonal wave oscillons in the DSD structures
, we obtain the diagonal wave oscillons in the DSD structures
![]() (32)
(32)
Summation of (32) yields a diagonal group oscillon
![]() (33)
(33)
where an amplitude produced by wave numbers
![]() (34)
(34)
The triangular summation of the diagonal group oscillons results in a diagonal energy oscillon
![]() (35)
(35)
which gives a cumulative energy of all diagonal group oscillons.
So, summation of constituents ![]() (12) of the kinetic energy is completed with the following result:
(12) of the kinetic energy is completed with the following result:
![]() (36)
(36)
If ![]() , then the diagonal wave oscillons (32) are converted into the doubled wave pulsons of propagation (27) and the diagonal group oscillon (33) becomes equal to the doubled group pulson of propagation (28).
, then the diagonal wave oscillons (32) are converted into the doubled wave pulsons of propagation (27) and the diagonal group oscillon (33) becomes equal to the doubled group pulson of propagation (28).
2.4. Wave, Group, and Energy Oscillons of Internal Interaction
General terms of the internal sums of (23)-(24) correspond to wave oscillons of internal interaction (internal wave oscillons for brevity)
![]() (37)
(37)
In the DSD structures, the internal wave oscillons become
![]() (38)
(38)
Adding the internal wave oscillons, we get an internal group oscillon
![]() (39)
(39)
The diagonal summation of the internal group oscillon results in an internal energy oscillon
![]() (40)
(40)
which returns a cumulative energy of all internal group oscillons.
2.5. Wave, Group, and Energy Oscillons of Non-Diagonal External Interaction
General terms of the external sums of (23)-(24) correspond to wave oscillons of non-diagonal external interaction (external wave oscillons for brevity)
![]() (41)
(41)
Using (26) and Equation (26) with ![]() , we compute the external wave oscillons via the DSD structures
, we compute the external wave oscillons via the DSD structures
![]() (42)
(42)
An external group oscillon takes the following form:
![]() (43)
(43)
where amplitudes generated by the wave numbers
![]() (44)
(44)
We then imply the triangular summation of the external group oscillons to find an external energy oscillon
![]() (45)
(45)
which demonstrates a cumulative energy of all external group oscillons.
Thus, summation of constituents ![]() (13) of the kinetic energy is finished as follows:
(13) of the kinetic energy is finished as follows:
![]() (46)
(46)
If ![]() , then the external wave oscillons (42) are transformed into the doubled internal wave oscillons (38) and the external group oscillon (43) becomes equal to the doubled internal group oscillon (39).
, then the external wave oscillons (42) are transformed into the doubled internal wave oscillons (38) and the external group oscillon (43) becomes equal to the doubled internal group oscillon (39).
2.6. Elementary Oscillons and Pulsons
Members of the ![]() th family of elementary oscillons of propagation of the velocity potential
th family of elementary oscillons of propagation of the velocity potential
![]() (47)
(47)
are defined via the weighted experimental DSK structures (1) of [3]
![]() (48)
(48)
where ![]() ,
, ![]() are functional amplitudes, 3-d DSK functions
are functional amplitudes, 3-d DSK functions ![]() are products
are products
![]() (49)
(49)
of the following 1-d (one-dimensional) DSK functions ![]() and an exponential function
and an exponential function ![]() :
:
![]() (50)
(50)
![]() (51)
(51)
In Equations (47)-(51), ![]() are the Cartesian coordinates of a motionless frame of reference, t is time,
are the Cartesian coordinates of a motionless frame of reference, t is time, ![]() are the Cartesian coordinates of a frame of reference moving with the
are the Cartesian coordinates of a frame of reference moving with the ![]() th elementary oscillon of propagation,
th elementary oscillon of propagation, ![]() is the celerity of propagation, and
is the celerity of propagation, and ![]() are reference values of
are reference values of ![]() at
at ![]() ,
, ![]() ,
, ![]() . A sign parameter
. A sign parameter ![]() for
for ![]() and
and ![]() for
for ![]() .
.
A wave oscillon of propagation of the velocity potential
![]() (52)
(52)
consists of the elementary oscillons of propagation.
Similarly, a group oscillon of propagation of the velocity potential
![]() (53)
(53)
is composed of the wave oscillons of propagation.
The wave pulsons and oscillons and the group pulsons and oscillons of the kinetic energy are constructed of elementary pulsons and oscillons of the kinetic energy.
Four elementary pulsons of propagation in the DSD structures for ![]() are defined by
are defined by
![]() (54)
(54)
The wave pulsons of propagation (27) and the group pulson of propagation (28) then become the following superpositions of the elementary pulsons of propagation:
![]() (55)
(55)
and
![]() (56)
(56)
There are six elementary oscillons of internal interaction (internal elementary oscillons for brevity) between members of the ![]() th family of the elementary oscillons of propagation for
th family of the elementary oscillons of propagation for ![]()
![]() (57)
(57)
The internal wave oscillons (38) and the internal group oscillon (39) are decomposed via the internal elementary oscillons as follows:
![]() (58)
(58)
and
![]() (59)
(59)
There are four elementary oscillons of diagonal external interaction (diagonal elementary oscillons for brevity) between members of the ![]() th and
th and ![]() th families of the elementary oscillons of propagation from the same wave groups with
th families of the elementary oscillons of propagation from the same wave groups with ![]() and
and ![]()
![]() (60)
(60)
The diagonal wave oscillons (32) and the diagonal group oscillon (33) then are subsequent superpositions of the diagonal elementary oscillons:
![]() (61)
(61)
and
![]() (62)
(62)
Eventually, there are six elementary oscillons of non-diagonal external interaction (external elementary oscillons for brevity) between members of the ![]() th and
th and ![]() th families of the elementary oscillons of propagation from distinct pairs of wave groups with
th families of the elementary oscillons of propagation from distinct pairs of wave groups with ![]() and
and ![]()
![]() (63)
(63)
The external wave oscillons (42) and the external group oscillon (43) are decomposed in terms of the external elementary oscillons in the following way:
![]() (64)
(64)
and
![]() (65)
(65)
If ![]() , then the diagonal elementary oscillons (60) are reduced to the doubled elementary pulsons of propagation (54) and then the external elementary oscillons (63) are transformed into the doubled internal elementary oscillons (57).
, then the diagonal elementary oscillons (60) are reduced to the doubled elementary pulsons of propagation (54) and then the external elementary oscillons (63) are transformed into the doubled internal elementary oscillons (57).
2.7. Summary of the Deterministic Quantization
Finally, we summarize quantization of the kinetic energy of the deterministic chaos of exponential oscillons and pulsons. The cumulative pulson of the kinetic energy (11) (the cumulative energy pulson for brevity) may be decomposed as follows:
![]() (66)
(66)
where ![]() is the energy pulson of propagation (30),
is the energy pulson of propagation (30), ![]() is the internal energy oscillon (40),
is the internal energy oscillon (40), ![]() is the diagonal energy oscillon (35), and
is the diagonal energy oscillon (35), and ![]() is the external energy oscillon (45).
is the external energy oscillon (45).
The energy pulson and the energy oscillons are composed of the group pulsons and the group oscillons, respectively. The group pulson of propagation ![]() (28) is composed of four wave pulsons of propagation
(28) is composed of four wave pulsons of propagation ![]() (27) that describe a vector self-interaction of velocity fields of
(27) that describe a vector self-interaction of velocity fields of ![]() th elementary oscillons of propagation (47) from four wave groups
th elementary oscillons of propagation (47) from four wave groups ![]() , respectively, for
, respectively, for ![]() .
.
The internal group oscillon ![]() (39) consists of six internal wave oscillons
(39) consists of six internal wave oscillons ![]() (38) that express a vector internal interaction of velocity fields of
(38) that express a vector internal interaction of velocity fields of ![]() th elementary oscillons of propagation from the distinct wave groups
th elementary oscillons of propagation from the distinct wave groups ![]() , correspondingly, for
, correspondingly, for ![]() .
.
The diagonal group oscillon ![]() (33) is constructed of four diagonal wave oscillons
(33) is constructed of four diagonal wave oscillons ![]() (32) that describe a vector external interaction of velocity fields of
(32) that describe a vector external interaction of velocity fields of ![]() th and
th and ![]() th elementary oscillons of propagation from the selfsame wave groups
th elementary oscillons of propagation from the selfsame wave groups ![]() for
for ![]() ,
, ![]() .
.
The external group oscillon ![]() (43) includes six external wave oscillons
(43) includes six external wave oscillons ![]() (42) that express a vector external interaction of velocity fields of
(42) that express a vector external interaction of velocity fields of ![]() th and
th and ![]() th elementary oscillons of propagation from the distinct pairs of wave groups
th elementary oscillons of propagation from the distinct pairs of wave groups ![]() &
& ![]() ,
, ![]() &
& ![]() ,
, ![]() &
& ![]() ,
, ![]() &
& ![]() ,
, ![]() &
& ![]() ,
, ![]() &
& ![]() , respectively, for
, respectively, for ![]() ,
, ![]() .
.
The wave pulsons of propagation (27) are composed of four elementary pulsons of propagation ![]() (54) that describe a scalar self-interaction of
(54) that describe a scalar self-interaction of ![]() th elementary oscillons of propagation from four wave groups with the velocity potentials
th elementary oscillons of propagation from four wave groups with the velocity potentials ![]() , respectively, for
, respectively, for ![]() .
.
The internal wave oscillons (38) consist of six internal elementary oscillons ![]() (57) that express a scalar internal interaction of
(57) that express a scalar internal interaction of ![]() th elementary oscillons of propagation from the distinct wave groups with the velocity potentials
th elementary oscillons of propagation from the distinct wave groups with the velocity potentials ![]() &
& ![]() ,
, ![]() &
& ![]() ,
, ![]() &
& ![]() ,
, ![]() &
& ![]() ,
, ![]() &
& ![]() ,
, ![]() &
& ![]() , respectively, for
, respectively, for ![]() .
.
The diagonal wave oscillons (32) are constructed of four diagonal elementary oscillons ![]() (60) that describe a scalar external interaction of
(60) that describe a scalar external interaction of ![]() th and
th and ![]() th elementary oscillons of propagation from the selfsame wave groups with the velocity potentials
th elementary oscillons of propagation from the selfsame wave groups with the velocity potentials ![]() &
& ![]() ,
, ![]() &
& ![]() ,
, ![]() &
& ![]() ,
, ![]() &
& ![]() , correspondingly, for
, correspondingly, for ![]() ,
, ![]() .
.
The external wave oscillons (42) include six external elementary oscillons ![]() ,
, ![]() (63) that express a scalar external interaction of
(63) that express a scalar external interaction of ![]() th and
th and ![]() th elementary oscillons of propagation from the distinct pairs of wave groups with the velocity potentials
th elementary oscillons of propagation from the distinct pairs of wave groups with the velocity potentials ![]() &
& ![]() and
and ![]() &
& ![]() ,
, ![]() &
& ![]() and
and ![]() &
& ![]() ,
, ![]() &
& ![]() and
and ![]() &
& ![]() ,
, ![]() &
& ![]() and
and ![]() &
& ![]() ,
, ![]() &
& ![]() and
and ![]() &
& ![]() ,
, ![]() &
& ![]() and
and ![]() &
& ![]() , for
, for ![]() ,
, ![]() .
.
3. Elementary Oscillons and Pulsons
3.1. The Elementary Oscillons of Propagation
To clarify topology of the elementary oscillons of propagation in the x-direction, we separate variable x and recast (47)-(51) to the following x-form:
![]() (67)
(67)
where amplitudes
![]() (68)
(68)
are expressed via coefficients
![]() (69)
(69)
![]() (70)
(70)
are x-shifts in the motionless frame, and
![]() (71)
(71)
are Xm-shifts in the ![]() th moving frame.
th moving frame.
For any frozen ![]() , the elementary oscillons of propagation (47) are transformed into solo-frequency (1-f) neutral oscillons in x with wavenumber
, the elementary oscillons of propagation (47) are transformed into solo-frequency (1-f) neutral oscillons in x with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to ![]() , and x-shifts
, and x-shifts
![]() (72)
(72)
See classification of oscillons and pulsons in Section 3.5.
Let’s consider propagation velocity ![]() and period
and period ![]() as independent parameters. Then a wave number
as independent parameters. Then a wave number
![]() (73)
(73)
and a spatial period along the x-axis (an x-wavelength)
![]() (74)
(74)
Since integrals of sines and cosines of (67) over x-period ![]() vanish,
vanish,
![]() (75)
(75)
i.e. the elementary oscillons of propagation are neutral as the average over the x-period vanishes.
To display topology of the elementary oscillons of propagation in the y-direction, we separate variable y and transform (47)-(51) into the following y-form:
![]() (76)
(76)
where amplitudes
![]() (77)
(77)
are computed in terms of coefficients
![]() (78)
(78)
![]() (79)
(79)
are y-shifts in the motionless frame, and
![]() (80)
(80)
are Ym-shifts in the ![]() th moving frame.
th moving frame.
For any frozen ![]() , the elementary oscillons of propagation (47) are reduced to 1-f neutral oscillons in y with wavenumber
, the elementary oscillons of propagation (47) are reduced to 1-f neutral oscillons in y with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to ![]() , and y-shifts
, and y-shifts
![]() (81)
(81)
Since ![]() and
and ![]() are independent parameters, a wave number and a spatial period along the y-axis become
are independent parameters, a wave number and a spatial period along the y-axis become
![]() (82)
(82)
The elementary oscillons of propagation are also neutral in the y-direction because
![]() (83)
(83)
Topology of the elementary oscillons of propagation in time follows from the inhomogeneous Fourier t-form of (47)-(51)
![]() (84)
(84)
in terms of four trigonometric functions
![]() (85)
(85)
of two arguments
![]() (86)
(86)
In Equations (84)-(86),
![]() (87)
(87)
are amplitudes,
![]() (88)
(88)
are frequencies,
![]() (89)
(89)
are t-shifts,
![]() (90)
(90)
are x- and y-shifts, respectively.
For any frozen ![]() , the elementary oscillons of propagation (47) are converted into duet-frequency (2-f) neutral oscillons in t, which are generated by superpositions of sine waves
, the elementary oscillons of propagation (47) are converted into duet-frequency (2-f) neutral oscillons in t, which are generated by superpositions of sine waves ![]() and cosine waves
and cosine waves ![]() with frequencies
with frequencies ![]() , respectively, amplitudes proportional to
, respectively, amplitudes proportional to ![]() , and t-shifts depending on
, and t-shifts depending on
![]() (91)
(91)
Since temporal periods of ![]() and
and ![]() are equal to, respectively,
are equal to, respectively,
![]() (92)
(92)
a temporal period of the elementary oscillons of propagation
![]() (93)
(93)
where ![]() is a least common multiple of
is a least common multiple of ![]() and
and ![]() are integers.
are integers.
Because integrals of sine waves ![]() and cosine waves
and cosine waves ![]() over t-periods
over t-periods ![]() vanish, the elementary oscillons of propagation are neutral in time, as well, since
vanish, the elementary oscillons of propagation are neutral in time, as well, since
![]() (94)
(94)
The elementary oscillon of propagation ![]() with
with ![]() is visualized in Figure 1 for the following independent parameters:
is visualized in Figure 1 for the following independent parameters:
![]() (95)
(95)
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 1. The elementary oscillon of propagation Ko,b,3: (a)—Ko,b,3 (x) (67), (b)—Ko,b,3 (y) (76), (c)—Ko,b,3 (t) (84) for independent parameters (95).
In Figures 1-18, two adjacent x-, y- and t-periods are shown by dotted vertical lines.
The elementary oscillons of propagation are displayed via 1-f neutral oscillons in x with periods ![]() , in terms of 1-f neutral oscillons in y with periods
, in terms of 1-f neutral oscillons in y with periods ![]() , and by 2-f neutral oscillons in t with periods
, and by 2-f neutral oscillons in t with periods ![]() , five local t-maximums, and five local t-minimums, the numbers of which are specified by
, five local t-maximums, and five local t-minimums, the numbers of which are specified by ![]() .
.
In agreement with (67) and (74),
![]() (96)
(96)
So, x-extrema of the elementary oscillon ![]() , which are equal to
, which are equal to ![]() , correspond to x-zeroes of the x-complementary oscillon
, correspond to x-zeroes of the x-complementary oscillon ![]() and x-zeroes of
and x-zeroes of ![]() to x-extrema of
to x-extrema of ![]() , which are also equal to
, which are also equal to ![]() . Similarly, x-extrema of
. Similarly, x-extrema of ![]() , which are equal to
, which are equal to ![]() , correspond to x-zeroes of the x-complementary oscillon
, correspond to x-zeroes of the x-complementary oscillon ![]() and x-zeroes of
and x-zeroes of ![]() to x-extrema of
to x-extrema of ![]() , which are equal to
, which are equal to ![]() , as well.
, as well.
Because of (76) and (82),
![]() (97)
(97)
Thus, y-extrema of the elementary oscillon ![]() , which are equal to
, which are equal to ![]() , correspond to y-zeroes of the y-complementary oscillon
, correspond to y-zeroes of the y-complementary oscillon ![]() and y-zeroes of
and y-zeroes of ![]() to y-extrema of
to y-extrema of ![]() , which are also equal to
, which are also equal to ![]() . Analogously, y-extrema of
. Analogously, y-extrema of ![]() , which are equal to
, which are equal to ![]() , correspond to y-zeroes of the y-complementary oscillon
, correspond to y-zeroes of the y-complementary oscillon ![]() and y-zeroes of
and y-zeroes of ![]() to y-extrema of
to y-extrema of ![]() , which are equal to
, which are equal to ![]() , as well.
, as well.
3.2. Eigenfunctions of the Inhomogeneous Fourier Expansions in x and y
Consider the ![]() th and
th and ![]() th families of inhomogeneous x-eigenfunctions of propagation
th families of inhomogeneous x-eigenfunctions of propagation
![]() (98)
(98)
of four arguments
![]() (99)
(99)
which are parametrized by two wavenumbers ![]() and
and ![]() with
with ![]() and
and ![]() .
.
An x-matrix of external interaction ![]() between x-eigenfunctions of propagation of the
between x-eigenfunctions of propagation of the ![]() th and
th and ![]() th families takes the following form:
th families takes the following form:
![]() (100)
(100)
Because of the product rules for sine and cosine waves, there are 16 inhomogeneous x-eigenfunctions of external interaction
![]()
![]() (101)
(101)
of eight arguments
![]() (102)
(102)
which are parametrized by two wavenumbers
![]() (103)
(103)
with ![]() ,
, ![]() . Thus, the x-eigenfunctions of external interaction include sine and cosine waves of all possible combinations of x-wave-numbers and x-shifts.
. Thus, the x-eigenfunctions of external interaction include sine and cosine waves of all possible combinations of x-wave-numbers and x-shifts.
Computing products (100) of x-eigenfunctions of propagation yields the following expansions via the x-eigenfunctions of external interaction (101):
![]()
![]() (104)
(104)
If ![]() , then two wavenumbers of the x-eigenfunctions of external interaction (103) are reduced to a single degenerated wavenumber since
, then two wavenumbers of the x-eigenfunctions of external interaction (103) are reduced to a single degenerated wavenumber since
![]() (105)
(105)
Consequently, eight arguments (102) of the x-eigenfunctions of external interaction are transformed into four arguments as
![]() (106)
(106)
Therefore, we define the following four arguments of x-eigenfunctions of internal interaction:
![]() (107)
(107)
If ![]() , x-eigenfunctions of external interaction are converted into eight x-eigenfunctions because
, x-eigenfunctions of external interaction are converted into eight x-eigenfunctions because
![]()
![]() (108)
(108)
Thus, six x-eigenfunctions of internal interaction ![]() and two vertical shifts
and two vertical shifts ![]() are defined as follows:
are defined as follows:
![]() (109)
(109)
The x-matrix of internal interaction ![]() becomes a symmetrical one, namely,
becomes a symmetrical one, namely,
![]() (110)
(110)
Computing elements of the x-matrix of internal interaction via the x-eigen-functions of internal interaction (109) returns
![]() (111)
(111)
Computation of eigenfunctions of the inhomogeneous Fourier series in y coincides with the computation of the eigenfunctions of the inhomogeneous Fourier series in x up to the following substitutions:
![]() (112)
(112)
3.3. Eigenfunctions of the Inhomogeneous Fourier Expansions in t
Consider the ![]() th (85) and
th (85) and ![]() th families of inhomogeneous t-eigenfunctions of propagation
th families of inhomogeneous t-eigenfunctions of propagation
![]() (113)
(113)
of four arguments
![]() (114)
(114)
which are parametrized by four frequencies ![]() , and
, and ![]() with
with ![]() ,
, ![]() .
.
A t-matrix of external interaction ![]() between t-eigenfunctions of propagation of the
between t-eigenfunctions of propagation of the ![]() th and
th and ![]() th families takes the following form:
th families takes the following form:
![]() (115)
(115)
Due to the product rules for sine and cosine waves, there are eight arguments of t-eigenfunctions of external interaction
![]() (116)
(116)
which include all possible sums and differences of the arguments of t-eigenfunctions of propagation (114).
Consequently, there are 16 inhomogeneous t-eigenfunctions of external interaction
![]() (117)
(117)
of eight arguments
![]()
![]() (118)
(118)
which are parametrized by eight frequencies
![]() (119)
(119)
with ![]() ,
, ![]() .
.
Computation of elements of the t-matrix of external interaction (115) returns the following expansions in terms of the t-eigenfunctions of external interaction (117):
![]()
![]() (120)
(120)
If ![]() , then eight frequencies of the t-eigenfunctions of external interaction are reduced to four degenerated frequencies since
, then eight frequencies of the t-eigenfunctions of external interaction are reduced to four degenerated frequencies since
![]() (121)
(121)
So, we define four frequencies of t-eigenfunctions of internal interaction
![]() (122)
(122)
Consequently, eight arguments of the t-eigenfunctions of external interaction are transformed into four independent arguments as
![]() (123)
(123)
Thus, we define the following four arguments of t-eigenfunctions of internal interaction:
![]() (124)
(124)
If ![]() , 16 t-eigenfunctions of external interaction are converted into eight functions because
, 16 t-eigenfunctions of external interaction are converted into eight functions because
![]() (125)
(125)
Therefore, eight t-eigenfunctions of internal interaction are defined as follows:
![]() (126)
(126)
Substitution of (126) in (125) yields asymptotics of t-eigenfunctions of external interaction as ![]() approaches
approaches ![]()
![]() (127)
(127)
The t-matrix of internal interaction ![]() is a symmetrical one, viz.
is a symmetrical one, viz.
![]() (128)
(128)
Computing elements of the t-matrix of internal interaction via the t-eigenfunctions of internal interaction (126) gives
![]() (129)
(129)
3.4. The Elementary Pulsons of Propagation
In eigenfunctions ![]() (98) with
(98) with ![]() , the elementary oscillons of propagation of the velocity potential (47), (67) are represented as follows:
, the elementary oscillons of propagation of the velocity potential (47), (67) are represented as follows:
![]() (130)
(130)
Substitution of (130) in (54) gives
![]() (131)
(131)
Computing squares of ![]() by (111) in terms of the x-eigenfunctions of internal interaction
by (111) in terms of the x-eigenfunctions of internal interaction ![]() (109) yields
(109) yields
![]() (132)
(132)
For any frozen ![]() , the elementary pulsons of propagation are reduced to 1-f critical positive pulsons in x with wavenumber
, the elementary pulsons of propagation are reduced to 1-f critical positive pulsons in x with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to
![]() (133)
(133)
x-shifts (72), and energy shifts proportional to (133). The elementary pulsons of propagation are critical since they are produced by the complete squares of ![]() .
.
The x-period of the elementary pulsons of propagation
![]() (134)
(134)
Because integrals of ![]() and
and ![]() over
over ![]() vanish,
vanish,
![]() (135)
(135)
Integrals (135) show that two pairs of the elementary pulsons of propagation ![]() and
and ![]() on average transfer equal positive amounts of the kinetic energy along the x-axis.
on average transfer equal positive amounts of the kinetic energy along the x-axis.
Similarly, the elementary oscillons of propagation of the velocity potential may be written in the y-direction as
![]() (136)
(136)
Therefore, the elementary pulsons of propagation of the kinetic energy via ![]() become
become
![]() (137)
(137)
and in terms of ![]() take the following form:
take the following form:
![]() (138)
(138)
For any frozen ![]() , the elementary pulsons of propagation are transformed into 1-f critical positive pulsons in y with wavenumber
, the elementary pulsons of propagation are transformed into 1-f critical positive pulsons in y with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to
![]() (139)
(139)
y-shifts (81), and energy shifts proportional to (139). The elementary pulsons of propagation are also critical since they are formed by the complete squares of ![]() .
.
Since amplitudes and shifts do not effect periods, the y-period
![]() (140)
(140)
Because integrals of ![]() and
and ![]() over
over ![]() vanish,
vanish,
![]() (141)
(141)
Therefore, two pairs of the elementary pulsons of propagation ![]() and
and ![]() on average transfer equal positive amounts of the kinetic energy along the y-axis.
on average transfer equal positive amounts of the kinetic energy along the y-axis.
With the help of (54), (47), and (84), the elementary pulsons of propagation become the complete squares of trigonometric polynomials
![]() (142)
(142)
Expanding the trigonometric polynomials and substituting elements of the t-matrix of internal interaction (129) via the t-eigenfunctions of internal interaction (126) returns
![]() (143)
(143)
where
![]() (144)
(144)
For any frozen ![]() , the elementary pulsons of propagation are converted into at most quartet-frequency (4-f) critical positive pulsons in t, which are formed by superpositions of cosine waves
, the elementary pulsons of propagation are converted into at most quartet-frequency (4-f) critical positive pulsons in t, which are formed by superpositions of cosine waves ![]() with frequencies
with frequencies ![]() , correspondingly, amplitudes proportional to
, correspondingly, amplitudes proportional to
![]() (145)
(145)
t-shifts depending on (91), and energy shifts proportional to
![]() (146)
(146)
The elementary pulsons of propagation are critical as they are described by the complete squares of trigonometric polynomials (142).
Temporal periods ![]() of
of ![]() , respectively, are
, respectively, are
![]() (147)
(147)
Therefore, a temporal period of the elementary pulsons of propagation
![]() (148)
(148)
where ![]() are integers.
are integers.
Because integrals of cosine waves ![]() over
over ![]() vanish, averages of the elementary pulsons of propagation over
vanish, averages of the elementary pulsons of propagation over ![]() become
become
![]() (149)
(149)
Therefore, integral (149) validates that the elementary pulsons of propagation on average transfer in time the same positive amount of the kinetic energy.
The elementary pulson of propagation ![]() with
with ![]() , and
, and ![]() is shown in Figure 2 for independent parameters (95). The elementary pulsons
is shown in Figure 2 for independent parameters (95). The elementary pulsons ![]() are visualized by 1-f critical pulsons in x with periods
are visualized by 1-f critical pulsons in x with periods ![]() and in terms of 1-f critical pulsons in y with periods
and in terms of 1-f critical pulsons in y with periods ![]() .
.
The elementary pulsons ![]() are displayed as 4-f critical pulsons in t with periods
are displayed as 4-f critical pulsons in t with periods ![]() ,
, ![]() local t-maximums, and
local t-maximums, and ![]() local t-minimums, the numbers of which do not exceed or equal to
local t-minimums, the numbers of which do not exceed or equal to ![]() due to
due to ![]() merged t-maximums and t-minimums. The elementary pulsons
merged t-maximums and t-minimums. The elementary pulsons ![]() ,
, ![]() as 4-f critical pulsons in t with periods
as 4-f critical pulsons in t with periods ![]() ,
, ![]() local t-maximums, and
local t-maximums, and ![]() local t-minimums, the numbers of which do not exceed or equal to
local t-minimums, the numbers of which do not exceed or equal to ![]() because of
because of ![]() merged t-maximums and t-minimums.
merged t-maximums and t-minimums.
In the view of (131), (132), and (134),
![]() (150)
(150)
So, x-maximums of the elementary pulson ![]() , which are equal to
, which are equal to ![]() , correspond to x-zeroes of the x-complementary pulson
, correspond to x-zeroes of the x-complementary pulson ![]() and x-zeroes of
and x-zeroes of ![]() to x-maximums of
to x-maximums of ![]() , which are also equal to
, which are also equal to ![]() . Similarly, x-maximums of the elementary pulson
. Similarly, x-maximums of the elementary pulson ![]() , which are equal to
, which are equal to ![]() , correspond to x-zeroes of the x-complementary pulson
, correspond to x-zeroes of the x-complementary pulson ![]() and x-zeroes of
and x-zeroes of ![]() to x-maximums of
to x-maximums of ![]() , which are equal to
, which are equal to ![]() , as well.
, as well.
Due to (137), (138), and (140),
![]() (151)
(151)
Thus, y-maximums of the elementary pulson ![]() , which are equal to
, which are equal to ![]() , correspond to y-zeroes of the y-complementary pulson
, correspond to y-zeroes of the y-complementary pulson ![]() and y-zeroes of
and y-zeroes of ![]() to y-maximums of
to y-maximums of ![]() , which are also equal to
, which are also equal to ![]() . Analogously, y-maximums of the elementary pulson
. Analogously, y-maximums of the elementary pulson ![]() , which are equal to
, which are equal to ![]() , correspond to y-zeroes of the y-complementary pulson
, correspond to y-zeroes of the y-complementary pulson ![]() and y-zeroes of
and y-zeroes of ![]() to y-maximums of
to y-maximums of ![]() , which are also equal to
, which are also equal to ![]() .
.
![]()
Figure 2. The elementary pulson of propagation Kp,b,3,b,3: (a)—Kp,b,3,b,3 (x) (132), (b)—Kp,b,3,b,3 (y) (138), (c)—Kp,b,3,b,3 (t) (143) for independent parameters (95).
3.5. The Internal Elementary Oscillons
Expressing definitions (57) in the x-eigenfunctions ![]() (98) with
(98) with ![]() and using the x-matrix of internal interaction (111) yields the internal elementary oscillons via the x-eigenfunctions of internal interaction
and using the x-matrix of internal interaction (111) yields the internal elementary oscillons via the x-eigenfunctions of internal interaction ![]() (109) in the following form:
(109) in the following form:
![]() (152)
(152)
For any frozen ![]() , the first pair
, the first pair ![]() of internal elementary oscillons is reduced to 1-f neutral oscillons in x, which are formed by sine waves
of internal elementary oscillons is reduced to 1-f neutral oscillons in x, which are formed by sine waves ![]() with wavenumber
with wavenumber ![]() . The second pair
. The second pair ![]() and the third pair
and the third pair ![]() are presented by 1-f nonneutral oscillons in x, which are generated by cosine wave
are presented by 1-f nonneutral oscillons in x, which are generated by cosine wave ![]() and sine wave
and sine wave ![]() with wavenumber
with wavenumber ![]() and energy shifts proportional to
and energy shifts proportional to
![]() (153)
(153)
For the first pair, amplitudes are proportional to (133) and x-shifts are specified by (72), for the second and third pairs amplitudes are proportional to ![]() and x-shifts depend on (72). The x-period of the internal elementary oscillons coincides with the x-period of the elementary pulsons of propagation (134).
and x-shifts depend on (72). The x-period of the internal elementary oscillons coincides with the x-period of the elementary pulsons of propagation (134).
Since integrals of ![]() for
for ![]() over
over ![]() vanish,
vanish,
![]() (154)
(154)
It is at tedious but a straightforward procedure to show that
![]() (155)
(155)
where trigonometric functions of the double argument
![]() (156)
(156)
Integrals (154) show that the first pair of internal elementary oscillons does not transfer on average any kinetic energy, the internal elementary oscillons of the second pair transfer on average equal amounts of the kinetic energy of the same sign, and the internal elementary oscillons of the third pair transfer on average equal amounts of the kinetic energy of opposite signs along the x-axis.
For two vector fields ![]() and
and ![]() , a scalar field of the kinetic energy of interaction is given by
, a scalar field of the kinetic energy of interaction is given by
![]() (157)
(157)
By the definition of the dot product
![]() (158)
(158)
where ![]() is an angle between vector fields
is an angle between vector fields ![]() and
and ![]() at a point
at a point ![]() .
.
So, the maximal magnitude of ![]()
![]() (159)
(159)
does not depend on ![]() , but the sign of
, but the sign of ![]() is determined by
is determined by ![]() . If the vector fields
. If the vector fields ![]() and
and ![]() are unidirectional at
are unidirectional at ![]() , then
, then ![]() . If the vector fields have opposite directions, then
. If the vector fields have opposite directions, then ![]() . The kinetic energy of interaction vanishes, if the vector fields
. The kinetic energy of interaction vanishes, if the vector fields ![]() and
and ![]() are orthogonal at
are orthogonal at ![]() .
.
Thus, ![]() becomes negative if
becomes negative if ![]() on the contrary to the kinetic energy of propagation of the vector field
on the contrary to the kinetic energy of propagation of the vector field ![]()
![]() (160)
(160)
that is always positively defined. To summarize, the scalar field of the kinetic energy of propagation ![]() has a pulsatory nature and the scalar field of the kinetic energy of interaction
has a pulsatory nature and the scalar field of the kinetic energy of interaction ![]() an oscillatory one.
an oscillatory one.
Let a nonlinear wave ![]() with an energy shift
with an energy shift ![]() and amplitudes
and amplitudes ![]() be decomposed into the inhomogeneous Fourier expansion via M cosine waves and sine waves with wavenumbers
be decomposed into the inhomogeneous Fourier expansion via M cosine waves and sine waves with wavenumbers ![]() and
and ![]() -shifts proportional to
-shifts proportional to ![]()
![]() (161)
(161)
such that
![]() (162)
(162)
Then a period of ![]() in a variable
in a variable ![]()
![]() (163)
(163)
and the average of ![]() over period
over period ![]()
![]() (164)
(164)
An oscillon ![]() is termed a neutral oscillon, if the average of
is termed a neutral oscillon, if the average of ![]() over
over ![]() vanishes, i.e.
vanishes, i.e. ![]() . So, the neutral oscillon doesn’t transfer the kinetic energy along the
. So, the neutral oscillon doesn’t transfer the kinetic energy along the ![]() -direction.
-direction.
An oscillon ![]() is called a positive (nonneutral) oscillon, if the average of
is called a positive (nonneutral) oscillon, if the average of ![]() over
over ![]() is positive since
is positive since ![]() and the nonneutral oscillon transfers the positive amount
and the nonneutral oscillon transfers the positive amount ![]() of the kinetic energy along the
of the kinetic energy along the ![]() -direction.
-direction.
When ![]() , the positive oscillon is transformed into a critical positive pulson, which also transfers the positive amount
, the positive oscillon is transformed into a critical positive pulson, which also transfers the positive amount ![]() of the kinetic energy along the
of the kinetic energy along the ![]() -direction. If
-direction. If ![]() , the critical positive pulson is converted into a supercritical pulson, which transfers the positive amount
, the critical positive pulson is converted into a supercritical pulson, which transfers the positive amount ![]() of the kinetic energy along the
of the kinetic energy along the ![]() -direction, as well.
-direction, as well.
Similarly, an oscillon ![]() is named a negative (nonneutral) oscillon, if the average of
is named a negative (nonneutral) oscillon, if the average of ![]() over
over ![]() is negative because
is negative because ![]() and the nonneutral oscillon transfers the negative amount
and the nonneutral oscillon transfers the negative amount ![]() of the kinetic energy along the
of the kinetic energy along the ![]() -direction.
-direction.
When ![]() , the negative oscillon is transformed into a critical negative pulson, which also transfers the negative amount
, the negative oscillon is transformed into a critical negative pulson, which also transfers the negative amount ![]() of the kinetic energy along the
of the kinetic energy along the ![]() -direction. If
-direction. If ![]() , the critical negative pulson is converted into a subcritical pulson, which transfers the negative amount
, the critical negative pulson is converted into a subcritical pulson, which transfers the negative amount ![]() of the kinetic energy along the
of the kinetic energy along the ![]() -direction, as well.
-direction, as well.
We then represent definitions (57) in the y-eigenfunctions ![]() with
with ![]() and use the y-matrix of internal interaction to compute the internal elementary oscillons in terms of the y-eigenfunctions of internal interaction
and use the y-matrix of internal interaction to compute the internal elementary oscillons in terms of the y-eigenfunctions of internal interaction ![]() as follows
as follows
![]() (165)
(165)
For any frozen ![]() , the first pair
, the first pair ![]() and the third pair
and the third pair ![]() of internal elementary oscillons are represented by 1-f nonneutral oscillons in y, which are generated by cosine wave
of internal elementary oscillons are represented by 1-f nonneutral oscillons in y, which are generated by cosine wave ![]() and sine wave
and sine wave ![]() with wavenumber
with wavenumber ![]() and energy shifts proportional to
and energy shifts proportional to
![]() (166)
(166)
The second pair ![]() is transformed into 1-f neutral oscillons in y, which are formed by sine waves
is transformed into 1-f neutral oscillons in y, which are formed by sine waves ![]() with wavenumber
with wavenumber ![]() . For the first and third pairs, amplitudes are proportional to
. For the first and third pairs, amplitudes are proportional to ![]() and y-shifts depend on (81). For the second pair, amplitudes are proportional to (139) and y-shifts are specified by (81). The y-period of the internal elementary oscillons equals to the y-period of the elementary pulsons of propagation (140).
and y-shifts depend on (81). For the second pair, amplitudes are proportional to (139) and y-shifts are specified by (81). The y-period of the internal elementary oscillons equals to the y-period of the elementary pulsons of propagation (140).
Because integrals of ![]() for
for ![]() over the period
over the period ![]() vanish,
vanish,
![]() (167)
(167)
It may be shown that
![]() (168)
(168)
where trigonometric functions of the double argument
![]() (169)
(169)
Thus, the internal elementary oscillons of the first pair transfer on average equal amounts of the kinetic energy of the same sign, the second pair of internal elementary oscillons on average does not transfer on average any kinetic energy, and the internal elementary oscillons of the third pair transfer on average equal amounts of the kinetic energy of opposite signs along the y-axis.
Usage of definitions (57) together with trigonometric polynomials (84) in t-eigenfunctions (113) and application of the t-matrix of internal interaction (129) yields the internal elementary oscillons in terms of the t-eigenfunctions of internal interaction (126) in the following t-form:
![]() (170)
(170)
where
![]() (171)
(171)
For any frozen ![]() , the first pair
, the first pair ![]() of internal elementary oscillons is presented by at most trio-frequency (3-f) neutral oscillons in t, which are produced by superpositions of sine waves
of internal elementary oscillons is presented by at most trio-frequency (3-f) neutral oscillons in t, which are produced by superpositions of sine waves ![]() with frequencies
with frequencies ![]() , correspondingly. The second pair
, correspondingly. The second pair ![]() is represented by at most 3-f neutral oscillons in t, which are generated by superpositions of sine waves
is represented by at most 3-f neutral oscillons in t, which are generated by superpositions of sine waves ![]() with frequencies
with frequencies ![]() , respectively. The third pair
, respectively. The third pair ![]() is formed by 2-f nonneutral oscillons in t, which are created by superpositions of cosine waves
is formed by 2-f nonneutral oscillons in t, which are created by superpositions of cosine waves ![]() with frequencies
with frequencies ![]() , correspondingly, and energy shifts proportional to
, correspondingly, and energy shifts proportional to ![]() . For all pairs, amplitudes are proportional to (145) and t-shifts depend on (91).
. For all pairs, amplitudes are proportional to (145) and t-shifts depend on (91).
A temporal period of the first pair
![]() (172)
(172)
where ![]() are integers and
are integers and ![]() are given by (147).
are given by (147).
Similarly, a temporal period of the second pair
![]() (173)
(173)
where ![]() are integers.
are integers.
Analogously, a temporal period of the third pair
![]() (174)
(174)
where ![]() are integers.
are integers.
Because integrals of ![]() over
over ![]() vanish, averages of the internal elementary oscillons over the relevant t-periods become
vanish, averages of the internal elementary oscillons over the relevant t-periods become
![]() (175)
(175)
Therefore, the first and second pairs of internal elementary oscillons do not transfer on average any kinetic energy in time, the internal elementary oscillons of the third pair on average transfer in time equal amounts of the kinetic energy of the opposite signs.
The internal elementary oscillon ![]() with
with ![]() is visualized in Figure 3 for independent parameters (95). The first pair is displayed by 1-f neutral oscillons in x with periods
is visualized in Figure 3 for independent parameters (95). The first pair is displayed by 1-f neutral oscillons in x with periods ![]() , the second and third pairs via 1-f nonneutral oscillons in x with periods
, the second and third pairs via 1-f nonneutral oscillons in x with periods ![]() .
.
The first and third pairs are visualized in terms of 1-f nonneutral oscillons in y with periods ![]() and the second pair by 1-f neutral oscillons in y with periods
and the second pair by 1-f neutral oscillons in y with periods ![]() .
.
The first pair is shown by 3-f neutral oscillons in t with periods ![]() ,
, ![]() local t-maximums, and
local t-maximums, and ![]() local t-minimums, the numbers of which do not exceed or equal to
local t-minimums, the numbers of which do not exceed or equal to ![]() due to
due to ![]() merged t-maximums and t-minimums, respectively. The second pair is visualized via 3-f neutral oscillons in t with periods
merged t-maximums and t-minimums, respectively. The second pair is visualized via 3-f neutral oscillons in t with periods ![]() ,
, ![]() local t-maximums, and
local t-maximums, and ![]() local t-minimums, the numbers of which do not exceed or equal to
local t-minimums, the numbers of which do not exceed or equal to ![]() due to
due to ![]() merged t-maximums and t-minimums. The third pair is displayed in terms of 2-f neutral oscillons in t with periods
merged t-maximums and t-minimums. The third pair is displayed in terms of 2-f neutral oscillons in t with periods ![]() ,
, ![]() local t-maximums, and
local t-maximums, and ![]() local t-minimums, the numbers of which are indicated by
local t-minimums, the numbers of which are indicated by ![]() .
.
In agreement with (152),
![]() (176)
(176)
Locations of x-maximums of ![]() coincide with locations of x-minimums of
coincide with locations of x-minimums of ![]() and locations of x-minimums of
and locations of x-minimums of ![]() coincide with locations of x-maximums of
coincide with locations of x-maximums of ![]() . Locations of x-maximums and x-minimums of
. Locations of x-maximums and x-minimums of ![]() coincide with locations of x-maximums and x-minimums of
coincide with locations of x-maximums and x-minimums of ![]() .
.
Because of (165),
![]() (177)
(177)
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 3. The internal elementary oscillon Ko,a,3,b,3: (a)—Ko,a,3,b,3 (x) (152), (b)—Ko,a,3,b,3 (y) (165), (c)—Ko,a,3,b,3 (t) (170) for independent parameters (95).
Locations of y-maximums of ![]() coincide with locations of y-minimums of
coincide with locations of y-minimums of ![]() and locations of y-minimums of
and locations of y-minimums of ![]() coincide with locations of y-maximums of
coincide with locations of y-maximums of ![]() . Locations of y-maximums and y-minimums of
. Locations of y-maximums and y-minimums of ![]() coincide with locations of y-maximums and y-minimums of
coincide with locations of y-maximums and y-minimums of ![]() .
.
Due to (170),
![]() (178)
(178)
Locations of t-maximums and t-minimums of ![]() coincide with locations of t-maximums and t-minimums of
coincide with locations of t-maximums and t-minimums of ![]() .
.
3.6. The Diagonal Elementary Oscillons
Using (130), we recast definitions (60) of the diagonal elementary oscillons in terms of x-eigenfunctions ![]() (98) and convert them with the help of the x-matrix of external interaction (104) into the following form:
(98) and convert them with the help of the x-matrix of external interaction (104) into the following form:
![]() (179)
(179)
For any frozen ![]() , the diagonal elementary oscillons are transformed into 2-f neutral oscillons in x, which are produced by superpositions of two pairs of cosine waves
, the diagonal elementary oscillons are transformed into 2-f neutral oscillons in x, which are produced by superpositions of two pairs of cosine waves ![]() and
and ![]() with two wavenumbers
with two wavenumbers ![]() , respectively, amplitudes proportional to
, respectively, amplitudes proportional to
![]() (180)
(180)
and x-shifts depending on
![]() (181)
(181)
If ![]() , the diagonal elementary oscillons (179) are reduced to the doubled elementary pulsons of propagation (132) in the view of (108)-(109).
, the diagonal elementary oscillons (179) are reduced to the doubled elementary pulsons of propagation (132) in the view of (108)-(109).
A spatial period of the diagonal elementary oscillons along the x-axis
![]() (182)
(182)
where
![]() (183)
(183)
are x-periods of ![]() and
and ![]() , respectively, and
, respectively, and ![]() are integers.
are integers.
Because integrals of ![]() for
for ![]() over
over ![]() vanish and integrals of
vanish and integrals of ![]() for
for ![]() over
over ![]() also vanish, averages of the diagonal elementary oscillons over
also vanish, averages of the diagonal elementary oscillons over ![]() vanish since
vanish since
![]() (184)
(184)
in the view of (179), (182) and the additive interval property. The diagonal elementary oscillons are neutral since on average they do not transfer any kinetic energy along the x-axis.
Similarly, representation of definitions (60) in y-eigenfunctions ![]() with the help of (136) and transformation into y-eigenfunctions of external interaction
with the help of (136) and transformation into y-eigenfunctions of external interaction ![]() yield
yield
![]() (185)
(185)
For any frozen ![]() , the diagonal elementary oscillons are transformed into 2-f neutral oscillons in y, which are formed by superpositions of two pairs of cosine waves
, the diagonal elementary oscillons are transformed into 2-f neutral oscillons in y, which are formed by superpositions of two pairs of cosine waves ![]() and
and ![]() with wavenumbers
with wavenumbers ![]() , respectively, amplitudes proportional to
, respectively, amplitudes proportional to
![]() (186)
(186)
and y-shifts depending on
![]() (187)
(187)
If ![]() , the diagonal elementary oscillons (185) are reduced to the doubled elementary pulsons of propagation (138).
, the diagonal elementary oscillons (185) are reduced to the doubled elementary pulsons of propagation (138).
A y-period of the diagonal elementary oscillons
![]() (188)
(188)
where
![]() (189)
(189)
are y-periods of ![]() and
and ![]() , respectively, and
, respectively, and ![]() are integers.
are integers.
In the view of vanishing integrals of ![]() for
for ![]() over
over ![]() and vanishing integrals of
and vanishing integrals of ![]() for
for ![]() over
over ![]() ,
,
![]() (190)
(190)
The diagonal elementary oscillons are also neutral along the y-axis since on average they do not transfer any kinetic energy.
In agreement with (60), (47), (84), we use the t-matrix of external interaction (120) to compute the inhomogeneous Fourier expansion of the diagonal elementary oscillons via the t-eigenfunctions of external interaction (117) as follows:
![]()
![]() (191)
(191)
For any frozen ![]() , the diagonal elementary oscillons are transformed into at most octet-frequency (8-f) neutral oscillons in t, which are produced by superpositions of cosine waves
, the diagonal elementary oscillons are transformed into at most octet-frequency (8-f) neutral oscillons in t, which are produced by superpositions of cosine waves ![]() with frequencies
with frequencies ![]() for
for ![]() , amplitudes proportional to
, amplitudes proportional to
![]() (192)
(192)
and t-shifts depending on
![]() (193)
(193)
If ![]() , the diagonal elementary oscillons (191) are reduced to the doubled elementary pulsons of propagation (143) due to (127).
, the diagonal elementary oscillons (191) are reduced to the doubled elementary pulsons of propagation (143) due to (127).
Since a t-period ![]() of
of ![]() for
for ![]() is
is
![]() (194)
(194)
a t-period of the diagonal elementary oscillons
![]() (195)
(195)
where ![]() are integers.
are integers.
In the view of vanishing integrals of ![]() over
over ![]() ,
,
![]() (196)
(196)
Integral (196) demonstrates that the diagonal elementary oscillons are neutral in time, as well, as they do not transfer on average any kinetic energy.
The diagonal elementary oscillon ![]() with
with ![]() is shown Figure 4 for independent parameters (95).
is shown Figure 4 for independent parameters (95).
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 4. The diagonal elementary oscillon Ko,b,2,b,3: (a)—Ko,b,2,b,3 (x) (179), (b)—Ko,b,2,b,3 (y) (185), (c)—Ko,b,2,b,3 (t) (191) for independent parameters (95).
Along the x-axis, the diagonal elementary oscillons are visualized by 2-f neutral oscillons in x with periods ![]() local x-maximums, and
local x-maximums, and ![]() x-local minimums, the numbers of which are specified by
x-local minimums, the numbers of which are specified by ![]() .
.
Along the y-axis, the diagonal elementary oscillons are displayed via 2-f neutral oscillons in y with periods ![]() local y-maximums, and
local y-maximums, and ![]() local y-minimums, the numbers of which are indicated by
local y-minimums, the numbers of which are indicated by ![]() .
.
The diagonal elementary oscillons ![]() are [7-f, 7-f, 6-f] neutral oscillons in t with periods
are [7-f, 7-f, 6-f] neutral oscillons in t with periods ![]() ,
, ![]() local t-maximums, and
local t-maximums, and ![]() local t-minimums, the numbers of which do not exceed or equal to
local t-minimums, the numbers of which do not exceed or equal to ![]() due to
due to ![]() merged t-maximums and t-minimums. The diagonal elementary oscillons
merged t-maximums and t-minimums. The diagonal elementary oscillons ![]() are [7-f, 7-f, 6-f] neutral oscillons in t with periods
are [7-f, 7-f, 6-f] neutral oscillons in t with periods ![]() ,
, ![]() local t-maximums, and
local t-maximums, and ![]() local t-minimums, the numbers of which do not exceed
local t-minimums, the numbers of which do not exceed ![]() due to
due to ![]() merged t-maximums and t-minimums.
merged t-maximums and t-minimums.
3.7. The External Elementary Oscillons
With the help of (130), we transform definitions (63) of the external elementary oscillons via x-eigenfunctions ![]() (98) and express them using the x-matrix of external interaction (104) as follows:
(98) and express them using the x-matrix of external interaction (104) as follows:
![]()
![]() (197)
(197)
For any frozen ![]() , the first pair
, the first pair ![]() of external elementary oscillons is reduced to 1-f neutral oscillons in x, which are formed by a pair of sine waves
of external elementary oscillons is reduced to 1-f neutral oscillons in x, which are formed by a pair of sine waves ![]() with wavenumber
with wavenumber ![]() . The second pair
. The second pair ![]() is transformed into 2-f neutral oscillons in x, which are generated by superpositions of two pairs of cosine waves
is transformed into 2-f neutral oscillons in x, which are generated by superpositions of two pairs of cosine waves ![]() and
and ![]() with wavenumbers
with wavenumbers ![]() , respectively. The third pair
, respectively. The third pair ![]() is converted into 2-f neutral oscillons in x, which are produced by superpositions of two pairs of sine waves
is converted into 2-f neutral oscillons in x, which are produced by superpositions of two pairs of sine waves ![]() and
and ![]() with wavenumbers
with wavenumbers ![]() , correspondingly.
, correspondingly.
For all three pairs, amplitudes are proportional to parameters (180) and x-shifts depend on parameters (181). The x-period of the first elementary pair is ![]() and the x-period of the second and third elementary pairs is
and the x-period of the second and third elementary pairs is ![]() that are defined by (182)-(183). If
that are defined by (182)-(183). If ![]() , the external elementary oscillons (197) are reduced to the doubled internal elementary oscillons (152) due to (108)-(109).
, the external elementary oscillons (197) are reduced to the doubled internal elementary oscillons (152) due to (108)-(109).
Averages over the x-period of six external elementary oscillons vanish since
![]() (198)
(198)
because of the same reasons as for the diagonal elementary oscillons (184). The external elementary oscillons are also neutral because on average they do not transfer any kinetic energy along the x-axis.
Analogously, definitions (63) written in y-eigenfunctions ![]() with the help of (136) and the y-matrix of external interaction give
with the help of (136) and the y-matrix of external interaction give
![]()
![]() (199)
(199)
For any frozen ![]() , the first pair
, the first pair ![]() of external elementary oscillons is transformed into 2-f neutral oscillons in y, which are generated by superpositions of two pairs of cosine waves
of external elementary oscillons is transformed into 2-f neutral oscillons in y, which are generated by superpositions of two pairs of cosine waves ![]() and
and ![]() with wavenumbers
with wavenumbers ![]() , correspondingly. The second pair
, correspondingly. The second pair ![]() is reduced to 1-f neutral oscillons in y, which are formed by a pair of sine waves
is reduced to 1-f neutral oscillons in y, which are formed by a pair of sine waves ![]() with wavenumber
with wavenumber ![]() . The third pair
. The third pair ![]() is converted into 2-f neutral oscillons in y, which are produced by superpositions of two pairs of sine waves
is converted into 2-f neutral oscillons in y, which are produced by superpositions of two pairs of sine waves ![]() and
and ![]() with wavenumbers
with wavenumbers ![]() , respectively.
, respectively.
For all pairs, amplitudes are proportional to parameters (186) and y-shifts depend on parameters (187). The y-period of the first and third elementary pairs is ![]() and the y-period of the second elementary pair is
and the y-period of the second elementary pair is ![]() that are specified by (188)-(189). If
that are specified by (188)-(189). If ![]() , the external elementary oscillons (199) are transformed into the doubled internal elementary oscillons (165).
, the external elementary oscillons (199) are transformed into the doubled internal elementary oscillons (165).
The external elementary oscillons are also neutral along the y-axis since on average they do not transfer any kinetic energy as
![]() (200)
(200)
With the help of (63), (47), and (84), we employ the t-matrix of external interaction (120) to compute the inhomogeneous Fourier expansion of the external elementary oscillons via the t-eigenfunctions of external interaction (117) in the following t-form:
![]()
![]() (201)
(201)
For any frozen ![]() , the first pair
, the first pair ![]() of external elementary oscillons is reduced to at most 4-f neutral oscillons in t, which are formed by superpositions of four sine waves
of external elementary oscillons is reduced to at most 4-f neutral oscillons in t, which are formed by superpositions of four sine waves ![]() with frequencies
with frequencies ![]() , respectively. The second pair
, respectively. The second pair ![]() is transformed into at most 4-f neutral oscillons in t, which are generated by superpositions of four sine waves
is transformed into at most 4-f neutral oscillons in t, which are generated by superpositions of four sine waves ![]() with frequencies
with frequencies ![]() , correspondingly. The third pair
, correspondingly. The third pair ![]() is converted into at most 4-f neutral oscillons in t, which are produced by superpositions of four cosine waves
is converted into at most 4-f neutral oscillons in t, which are produced by superpositions of four cosine waves ![]() with frequencies
with frequencies ![]() , respectively.
, respectively.
For all pairs, amplitudes are proportional to parameters (192) and t-shifts depend on parameters (193). If ![]() , the external elementary oscillons (201) are converted to the doubled internal elementary oscillons (170) because of (127).
, the external elementary oscillons (201) are converted to the doubled internal elementary oscillons (170) because of (127).
Temporal periods of the first pair
![]() (202)
(202)
the second pair
![]() (203)
(203)
and the third pair
![]() (204)
(204)
where ![]() ,
, ![]() are integers,
are integers, ![]() for
for ![]() are specified by (194).
are specified by (194).
Because integrals of sine waves ![]() over the relevant t-periods
over the relevant t-periods ![]() vanish for
vanish for ![]() , averages of the external elementary oscillons also vanish for the reason that
, averages of the external elementary oscillons also vanish for the reason that
![]() (205)
(205)
due to (201)-(204) and the additive interval property. In agreement with (205), the external elementary oscillons are also neutral because on average they do not transfer in time any kinetic energy.
The diagonal elementary oscillon ![]() with
with ![]() is shown in Figure 5 for independent parameters (95).
is shown in Figure 5 for independent parameters (95).
Along the x-axis, the first pair is visualized by 1-f neutral oscillons in x with periods ![]() . The second and third pairs are displayed by 2-f neutral oscillons in x with periods
. The second and third pairs are displayed by 2-f neutral oscillons in x with periods ![]() ,
, ![]() local x-maximums, and
local x-maximums, and ![]() local x-minimums, the numbers of which are specified by
local x-minimums, the numbers of which are specified by ![]() .
.
Along the y-axis, the first and third pairs are depicted by 2-f neutral oscillons in y with periods ![]() ,
, ![]() local y-maximums, and
local y-maximums, and ![]() local y-minimums, the numbers of which are indicated by
local y-minimums, the numbers of which are indicated by ![]() . The second pair is shown by 1-f neutral oscillons in y with periods
. The second pair is shown by 1-f neutral oscillons in y with periods ![]() .
.
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 5. The external elementary oscillon Ko,a,2,c,3: (a)—Ko,a,2,c,3 (x) (197), (b)—Ko,a,2,c,3 (y) (199), (c)—Ko,a,2,c,3 (t) (201) for independent parameters (95).
The first pair is presented by 4-f neutral oscillons in t with periods ![]() ,
, ![]() local t-maximums,
local t-maximums, ![]() local t-minimums, the numbers of which do not exceed or equal to
local t-minimums, the numbers of which do not exceed or equal to ![]() due to
due to ![]() merged t-maximums and t-minimums, respectively. The second pair is represented via [3-f, 4-f, 4-f] neutral oscillons in t with periods
merged t-maximums and t-minimums, respectively. The second pair is represented via [3-f, 4-f, 4-f] neutral oscillons in t with periods ![]() ,
, ![]() local t-maximums, and
local t-maximums, and ![]() local t-minimums, the numbers of which do not exceed or equal to
local t-minimums, the numbers of which do not exceed or equal to ![]() because of
because of ![]() merged t-maximums and t-minimums. The third pair is visualized by [4-f, 4-f, 3-f] neutral oscillons in t with periods
merged t-maximums and t-minimums. The third pair is visualized by [4-f, 4-f, 3-f] neutral oscillons in t with periods ![]() ,
, ![]() local t-maximums, and
local t-maximums, and ![]() local t-minimums, the numbers of which are provided by
local t-minimums, the numbers of which are provided by ![]() .
.
4. Wave Oscillons and Pulsons
4.1. The Wave Oscillon of Propagation
Separation of variable x in (52) gives
![]() (206)
(206)
where
![]() (207)
(207)
is an amplitude, which is expressed via coefficients
![]() (208)
(208)
In Equation (206),
![]() (209)
(209)
is an x-shift in the motionless frame and
![]() (210)
(210)
is an Xm-shift in the ![]() th moving frame.
th moving frame.
For any frozen ![]() , the wave oscillon of propagation is transformed into a 1-f neutral oscillon in x with the wavenumber
, the wave oscillon of propagation is transformed into a 1-f neutral oscillon in x with the wavenumber ![]() , an amplitude proportional to
, an amplitude proportional to ![]() and the x-shift
and the x-shift ![]() . The x-period
. The x-period ![]() of the wave oscillon of propagation coincides with (74).
of the wave oscillon of propagation coincides with (74).
The wave oscillon of propagation of the velocity potential is neutral in the x-direction since
![]() (211)
(211)
Proceeding with the same approach, we separate variable y in (52) to find
![]() (212)
(212)
where an amplitude
![]() (213)
(213)
is computed via coefficients
![]() (214)
(214)
In Equation (212),
![]() (215)
(215)
is a y-shift in the motionless frame and
![]() (216)
(216)
is an Ym-shift in the ![]() th moving frame.
th moving frame.
For any frozen ![]() , the wave oscillon of propagation is converted into a 1-f neutral oscillon in y with the wavenumber
, the wave oscillon of propagation is converted into a 1-f neutral oscillon in y with the wavenumber ![]() , an amplitude proportional to
, an amplitude proportional to ![]() and the y-shift
and the y-shift ![]() . The y-period
. The y-period ![]() of the wave oscillon of propagation is specified by (82).
of the wave oscillon of propagation is specified by (82).
The wave oscillon of propagation of the velocity potential is also neutral along the y-axis because
![]() (217)
(217)
Topology of the wave oscillon of propagation in time is described by the inhomogeneous Fourier t-expansion of (52)
![]() (218)
(218)
expressed via two trigonometric functions
![]() (219)
(219)
of two arguments
![]() (220)
(220)
In Equations (218), (220),
![]() (221)
(221)
are amplitudes and
![]() (222)
(222)
are t-shifts.
For any frozen ![]() , the wave oscillon of propagation is reduced to a 2-f neutral oscillon in t, which is formed by superpositions of sine waves
, the wave oscillon of propagation is reduced to a 2-f neutral oscillon in t, which is formed by superpositions of sine waves ![]() with frequencies
with frequencies ![]() , correspondingly, amplitudes proportional to
, correspondingly, amplitudes proportional to ![]() , and t-shifts depending on
, and t-shifts depending on ![]() ,
, ![]() . The t-period of the wave oscillon of propagation is given by (92)-(93).
. The t-period of the wave oscillon of propagation is given by (92)-(93).
Because integrals of sine waves ![]() over
over ![]() vanish, respectively, average of the wave oscillon of propagation over t-period
vanish, respectively, average of the wave oscillon of propagation over t-period ![]() vanishes, as well, since
vanishes, as well, since
![]() (223)
(223)
The wave oscillon of propagation ![]() with
with ![]() is visualized in Figure 6 for independent parameters (95). The wave oscillons of propagation
is visualized in Figure 6 for independent parameters (95). The wave oscillons of propagation ![]() are displayed by 1-f neutral oscillons in x with periods
are displayed by 1-f neutral oscillons in x with periods ![]() , via 1-f neutral oscillons in y with periods
, via 1-f neutral oscillons in y with periods ![]() , and through 2-f neutral oscillons in t with periods
, and through 2-f neutral oscillons in t with periods ![]() , 5 local t-maximums, and 5 local t-minimums, the numbers of which are specified by
, 5 local t-maximums, and 5 local t-minimums, the numbers of which are specified by ![]() .
.
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 6. The wave oscillon of propagation Kw,i,3: (a)—Kw,i,3 (x) (206), (b)—Kw,i,3 (y) (212), (c)—Kw,i,3 (t) (218) for independent parameters (95).
4.2. The Wave Pulsons of Propagation
Combining (55) and (132) yields that the wave pulsons of propagation (27) in terms of the x-eigenfunctions of internal interaction ![]() (109) become
(109) become
![]() (224)
(224)
For any frozen ![]() , the wave pulsons of propagation are reduced to 1-f supercritical pulsons in x, which are formed by a superposition of cosine waves
, the wave pulsons of propagation are reduced to 1-f supercritical pulsons in x, which are formed by a superposition of cosine waves ![]() with wavenumber
with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to ![]() and (133), x-shifts (72), and energy shifts depending on
and (133), x-shifts (72), and energy shifts depending on ![]() , and (133). Therefore, the x-period of the wave pulsons of propagation is specified by (134).
, and (133). Therefore, the x-period of the wave pulsons of propagation is specified by (134).
Since integrals of ![]() and
and ![]() over
over ![]() vanish,
vanish,
![]() (225)
(225)
Two pairs of the wave pulsons of propagation ![]() and
and ![]() ,
, ![]() on average transfer equal positive amounts of the kinetic energy along the x-axis.
on average transfer equal positive amounts of the kinetic energy along the x-axis.
Similarly, we combine (55) and (138) to compute the inhomogeneous Fourier expansion for the wave pulsons of propagation (27) via the y-eigenfunctions of internal interaction ![]() in the following form:
in the following form:
![]() (226)
(226)
For any frozen ![]() , the wave pulsons of propagation are converted into 1-f supercritical pulsons in y, which are produced by a superposition of cosine waves
, the wave pulsons of propagation are converted into 1-f supercritical pulsons in y, which are produced by a superposition of cosine waves ![]() with wavenumber
with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to ![]() and (139), y-shifts (81), and energy shifts depending on
and (139), y-shifts (81), and energy shifts depending on ![]() , and (139). Therefore, the y-period of the wave pulsons of propagation is specified by (140).
, and (139). Therefore, the y-period of the wave pulsons of propagation is specified by (140).
Because integrals of ![]() and
and ![]() over
over ![]() vanish,
vanish,
![]() (227)
(227)
So, two pairs of the wave pulsons of propagation ![]() and
and ![]() on average transfer equal positive amounts of the kinetic energy along the y-axis.
on average transfer equal positive amounts of the kinetic energy along the y-axis.
Substitution of (143) in (55) and collection of like terms results in the inhomogeneous Fourier expansion of the wave pulsons of propagation (27) through the t-eigenfunctions of internal interaction ![]() (126)
(126)
![]() (228)
(228)
For any frozen ![]() , the wave pulsons of propagation are transformed into 2-f supercritical pulsons in t, which are generated by superpositions of cosine waves
, the wave pulsons of propagation are transformed into 2-f supercritical pulsons in t, which are generated by superpositions of cosine waves ![]() with frequencies
with frequencies ![]() , respectively, amplitudes proportional to
, respectively, amplitudes proportional to ![]() , and (145), t-shifts depending on (91), and energy shifts proportional to
, and (145), t-shifts depending on (91), and energy shifts proportional to ![]() and (146).
and (146).
A temporal period of the wave pulsons of propagation
![]() (229)
(229)
where ![]() are integers and
are integers and ![]() given by (147).
given by (147).
Average of the wave pulsons of propagation over ![]() takes the following form:
takes the following form:
![]() (230)
(230)
Integral (230) validates that the wave pulsons of propagation on average transfer the same positive amount of the kinetic energy in time.
The wave pulson of propagation ![]() with
with ![]() is shown in Figure 7 for independent parameters (95). The wave pulsons of propagation are visualized by 1-f supercritical pulsons in x with periods
is shown in Figure 7 for independent parameters (95). The wave pulsons of propagation are visualized by 1-f supercritical pulsons in x with periods ![]() , through 1-f supercritical pulsons in y with periods
, through 1-f supercritical pulsons in y with periods ![]() , and via 2-f supercritical pulsons in t with periods
, and via 2-f supercritical pulsons in t with periods ![]() ,
, ![]() local t-maximums, and
local t-maximums, and ![]() local t-minimums, the numbers of which are specified by
local t-minimums, the numbers of which are specified by ![]() .
.
In agreement with (224),
![]()
Figure 7. The wave pulson of propagation Kw,b,3,b,3: (a)—Kw,b,3,b,3 (x) (224), (b)—Kw,b,3,b,3 (y) (226), (c)—Kw,b,3,b,3 (t) (228) for independent parameters (95).
![]() (231)
(231)
Therefore, x-maximums of ![]() correspond to x-minimums of
correspond to x-minimums of ![]() and x-minimums of
and x-minimums of ![]() to x-maximums of
to x-maximums of ![]() . Similarly, x-maximums of
. Similarly, x-maximums of ![]() correspond to x-minimums of
correspond to x-minimums of ![]() and x-minimums of
and x-minimums of ![]() to x-maximums of
to x-maximums of ![]() . Locations of x-maximums and x-minimums of
. Locations of x-maximums and x-minimums of ![]() coincide with locations of x-maximums and x-minimums of
coincide with locations of x-maximums and x-minimums of ![]() . Analogously, locations of x-maximums and x-minimums of
. Analogously, locations of x-maximums and x-minimums of ![]() match locations of x-maximums and x-minimums of
match locations of x-maximums and x-minimums of ![]() .
.
Due to (226),
![]() (232)
(232)
Consequently, y-maximums of ![]() correspond to y-minimums of
correspond to y-minimums of ![]() and y-minimums of
and y-minimums of ![]() to y-maximums of
to y-maximums of ![]() . Analogously, y-maximums of
. Analogously, y-maximums of ![]() correspond to y-minimums of
correspond to y-minimums of ![]() and y-minimums of
and y-minimums of ![]() to y-maximums of
to y-maximums of ![]() . Locations of y-maximums and y-minimums of
. Locations of y-maximums and y-minimums of ![]() match locations of y-maximums and y-minimums of
match locations of y-maximums and y-minimums of ![]() . Similarly, locations of y-maximums and y-minimums of
. Similarly, locations of y-maximums and y-minimums of ![]() coincide with locations of y-maximums and y-minimums of
coincide with locations of y-maximums and y-minimums of ![]() .
.
Because of (228),
![]() (233)
(233)
So, locations of t-maximums of ![]() and
and ![]() correspond to locations of t-minimums of
correspond to locations of t-minimums of ![]() and
and ![]() , respectively. Analogously, locations of t-minimums of
, respectively. Analogously, locations of t-minimums of ![]() and
and ![]() to locations of t-maximums of
to locations of t-maximums of ![]() and
and ![]() , correspondingly.
, correspondingly.
4.3. The Internal Wave Oscillons
Substituting (152) in (58) results in the inhomogeneous Fourier expansion of the internal wave oscillons (38) along the x-axis
![]() (234)
(234)
For any frozen ![]() , the first pair
, the first pair ![]() of internal wave oscillons is transformed into 1-f neutral oscillons in x, which is produced by a superposition of sine waves
of internal wave oscillons is transformed into 1-f neutral oscillons in x, which is produced by a superposition of sine waves ![]() with wavenumber
with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to ![]() and (133), and x-shifts (72). The second pair
and (133), and x-shifts (72). The second pair ![]() and the third pair
and the third pair ![]() are reduced to 0-f (uniform) noncritical pulsons in x with energy shifts proportional to
are reduced to 0-f (uniform) noncritical pulsons in x with energy shifts proportional to ![]() , and (153). The x-wavelength of the internal wave oscillons is given by (134).
, and (153). The x-wavelength of the internal wave oscillons is given by (134).
Averages over the x-wavelength of six internal wave oscillons
![]() (235)
(235)
prove that the first pair of internal wave oscillons on average does not transfer any kinetic energy along the x-axis, the internal wave oscillons of the second pair on average transfer along the x-axis equal amounts of the kinetic energy, and the internal wave oscillons of the third pair on average transfer along the x-axis equal amounts of the kinetic energy of opposite signs.
Analogously, we substitute (165) in (58) to find the inhomogeneous Fourier expansion of the internal wave oscillons along the y-axis
![]() (236)
(236)
For any frozen ![]() , the first pair
, the first pair ![]() and the third pair
and the third pair ![]() of internal wave oscillons are converted into 0-f noncritical pulsons in y with energy shifts proportional to
of internal wave oscillons are converted into 0-f noncritical pulsons in y with energy shifts proportional to ![]() , and (166). The second pair
, and (166). The second pair ![]() is reduced to 1-f neutral oscillons in y, which is formed by a superposition of sine waves
is reduced to 1-f neutral oscillons in y, which is formed by a superposition of sine waves ![]() with wavenumber
with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to ![]() and (139), and y-shifts (81). The y-wavelength of the internal wave oscillons is specified by (140).
and (139), and y-shifts (81). The y-wavelength of the internal wave oscillons is specified by (140).
The internal wave oscillons of the first pair on average transfer along the y-axis equal amounts of the kinetic energy, the second pair of internal wave oscillons on average does not transfer any kinetic energy along the y-axis, and the internal wave oscillons of the third pair on average transfer along the y-axis equal amounts of the kinetic energy of opposite signs because
![]() (237)
(237)
Substitution of (170) in (58) yields the inhomogeneous Fourier expansion of the internal wave oscillons in time
![]() (238)
(238)
For any frozen ![]() , the first pair
, the first pair ![]() and the second pair
and the second pair ![]() of internal wave oscillons are transformed into 1-f neutral oscillons in t, which are formed by sine waves
of internal wave oscillons are transformed into 1-f neutral oscillons in t, which are formed by sine waves ![]() with frequencies
with frequencies ![]() , respectively, amplitudes proportional to
, respectively, amplitudes proportional to ![]() , and (145), and t-shifts depending on (91). The temporal period of the first and second pairs are
, and (145), and t-shifts depending on (91). The temporal period of the first and second pairs are ![]() and
and ![]() , which are specified by (147). The third pair
, which are specified by (147). The third pair ![]() is transformed into 0-f noncritical pulsons with energy shifts depending on
is transformed into 0-f noncritical pulsons with energy shifts depending on ![]() .
.
For the same reasoning as for the internal elementary oscillons,
![]() (239)
(239)
Similar to the internal elementary oscillons (175), the first and second pairs of internal wave oscillons on average do not transfer in time any kinetic energy and the internal wave oscillons of the third pair transfer in time equal amounts of the kinetic energy of the opposite signs.
The internal wave oscillon ![]() with
with ![]() is visualized in Figure 8 for independent parameters (95). The first pair is displayed by 1-f neutral oscillons in x with periods
is visualized in Figure 8 for independent parameters (95). The first pair is displayed by 1-f neutral oscillons in x with periods ![]() , the second and third pairs via 0-f noncritical pulsons in x with periods
, the second and third pairs via 0-f noncritical pulsons in x with periods ![]() .
.
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 8. The internal wave oscillon Kw,a,3,b,3: (a)—Kw,a,3,b,3 (x) (234), (b)—Kw,a,3,b,3 (y) (236), (c)—Kw,a,3,b,3 (t) (238) for independent parameters (95).
In the y-direction, the first and third pairs are visualized by 0-f noncritical pulsons in y with periods ![]() and the second pair via 1-f neutral oscillons in y with periods
and the second pair via 1-f neutral oscillons in y with periods ![]() .
.
The first pair is represented by 1-f neutral oscillons in t with periods ![]() , the second pair via 1-f neutral oscillons in t with periods
, the second pair via 1-f neutral oscillons in t with periods ![]() , and the third pair in terms of 0-f noncritical pulsons in t with periods
, and the third pair in terms of 0-f noncritical pulsons in t with periods ![]() .
.
4.4. The Diagonal Wave Oscillons
Substituting (179) in (61), we convert definitions (32) into the inhomogeneous Fourier expansion of the diagonal wave oscillons along the x-axis
![]()
![]() (240)
(240)
where
![]() (241)
(241)
For any frozen ![]() , the diagonal wave oscillons are presented by 2-f neutral oscillons in x, which are formed by superpositions of two pairs of cosine waves
, the diagonal wave oscillons are presented by 2-f neutral oscillons in x, which are formed by superpositions of two pairs of cosine waves ![]() and
and ![]() with two wavenumbers
with two wavenumbers ![]() , respectively, amplitudes depending on
, respectively, amplitudes depending on ![]() , and (180), and x-shifts, which depend on (181). The x-wavelength of the diagonal wave oscillons is given by (182)-(183). If
, and (180), and x-shifts, which depend on (181). The x-wavelength of the diagonal wave oscillons is given by (182)-(183). If ![]() , the diagonal wave oscillons (240) are transformed by (108)-(109) into the doubled wave pulsons of propagation (224).
, the diagonal wave oscillons (240) are transformed by (108)-(109) into the doubled wave pulsons of propagation (224).
Similar to (184), the diagonal wave oscillons on average do not transfer any kinetic energy along the x-axis since
![]() (242)
(242)
Analogously, representation of definitions (32) in y-eigenfunctions of external interaction ![]() with the help of (185) and (61) yields
with the help of (185) and (61) yields
![]()
![]()
![]() (243)
(243)
For any frozen ![]() , the diagonal wave oscillons are transformed into 2-f neutral oscillons in y, which are produced by superpositions of two pairs of cosine waves
, the diagonal wave oscillons are transformed into 2-f neutral oscillons in y, which are produced by superpositions of two pairs of cosine waves ![]() and
and ![]() with two wavenumbers
with two wavenumbers ![]() , respectively, amplitudes, which depend on
, respectively, amplitudes, which depend on ![]() , and (186), and y-shifts depending on (187). The y-period of the diagonal wave oscillons is specified by (188)-(189). If
, and (186), and y-shifts depending on (187). The y-period of the diagonal wave oscillons is specified by (188)-(189). If ![]() , the diagonal wave oscillons (243) are reduced to the doubled wave pulsons of propagation (226).
, the diagonal wave oscillons (243) are reduced to the doubled wave pulsons of propagation (226).
Like the diagonal elementary oscillons (190), the diagonal wave oscillons are neutral along the y-axis because
![]() (244)
(244)
Substitution of (191) in (61) and collection of like terms produce the inhomogeneous Fourier expansion of the diagonal wave oscillons in time
![]()
![]() (245)
(245)
where
![]() (246)
(246)
are nonlinear amplitudes produced by various wavenumbers.
For any frozen ![]() , the diagonal wave oscillons are converted into at most 8-f neutral oscillons in t, which are generated by superpositions of cosine waves
, the diagonal wave oscillons are converted into at most 8-f neutral oscillons in t, which are generated by superpositions of cosine waves ![]() with frequencies
with frequencies ![]() for
for ![]() , amplitudes proportional to
, amplitudes proportional to ![]() , and (192), and t-shifts depending on (193). The t-period of the diagonal wave oscillons is also provided by (194)-(195). If
, and (192), and t-shifts depending on (193). The t-period of the diagonal wave oscillons is also provided by (194)-(195). If ![]() , the diagonal wave oscillons (245) are transformed into the doubled wave pulsons of propagation (228).
, the diagonal wave oscillons (245) are transformed into the doubled wave pulsons of propagation (228).
Since
![]() (247)
(247)
the diagonal wave oscillons on average do not transfer in time any kinetic energy, as well.
The diagonal wave oscillon ![]() with
with ![]() is shown in Figure 9 for independent parameters (95). The diagonal wave oscillons
is shown in Figure 9 for independent parameters (95). The diagonal wave oscillons ![]() are represented by 2-f neutral oscillons in x with periods
are represented by 2-f neutral oscillons in x with periods ![]() ,
, ![]() local x-maximums, and
local x-maximums, and ![]() local x-minimums, the numbers of which do not exceed or equal to
local x-minimums, the numbers of which do not exceed or equal to ![]() due to
due to ![]() merged x-maximums and x-minimums.
merged x-maximums and x-minimums.
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 9. The diagonal wave oscillon Kw,b,2,b,3: (a)—Kw,b,2,b,3 (x) (240), (b)—Kw,b,2,b,3 (y) (243), (c)—Kw,b,2,b,3 (t) (245) for independent parameters (95).
Along the y-axis, the diagonal wave oscillons ![]() are displayed by 2-f neutral oscillons in y with periods
are displayed by 2-f neutral oscillons in y with periods ![]() ,
, ![]() local y-maximums, and
local y-maximums, and ![]() local y-minimums, the numbers of which do not exceed or equal to
local y-minimums, the numbers of which do not exceed or equal to ![]() due to
due to ![]() merged y-maximums and y-minimums.
merged y-maximums and y-minimums.
There are three sets of frequencies with ![]() for [7-f, 7-f, 6-f] diagonal wave oscillons, since frequencies
for [7-f, 7-f, 6-f] diagonal wave oscillons, since frequencies ![]() are repeated in the first, second, and third sets, respectively. Due to smallness of amplitudes
are repeated in the first, second, and third sets, respectively. Due to smallness of amplitudes ![]() compared with
compared with ![]() ,
,
![]() (248)
(248)
the diagonal wave oscillons ![]() are visualized with a graph accuracy by [6-f, 5-f, 5-f] neutral oscillons in t with periods
are visualized with a graph accuracy by [6-f, 5-f, 5-f] neutral oscillons in t with periods ![]() ,
, ![]() local t-maximums, and
local t-maximums, and ![]() local t-minimums, the numbers of which do not exceed or equal to
local t-minimums, the numbers of which do not exceed or equal to ![]() due to
due to ![]() merged t-maximums and t-minimums.
merged t-maximums and t-minimums.
4.5. The External Wave Oscillons
Substituting (197) in (64), we recast definitions (42) in the inhomogeneous Fourier expansion of the external wave oscillons along the x-axis
![]()
![]() (249)
(249)
For any frozen ![]() , the first pair
, the first pair ![]() of external wave oscillons is reduced to 1-f neutral oscillons in x, which are formed by a superposition of sine waves
of external wave oscillons is reduced to 1-f neutral oscillons in x, which are formed by a superposition of sine waves ![]() with wavenumber
with wavenumber ![]() . The second pair
. The second pair ![]() is transformed into at most 2-f neutral oscillons in x, which are generated by superpositions of two pairs of cosine waves
is transformed into at most 2-f neutral oscillons in x, which are generated by superpositions of two pairs of cosine waves ![]() and
and ![]() with two wavenumbers
with two wavenumbers ![]() , respectively. The third pair
, respectively. The third pair ![]() is converted into at most 2-f neutral oscillons in x, which are produced by superpositions of two pairs of sine waves
is converted into at most 2-f neutral oscillons in x, which are produced by superpositions of two pairs of sine waves ![]() and
and ![]() with two wavenumbers
with two wavenumbers ![]() , correspondingly.
, correspondingly.
For the first pair, amplitudes depend on ![]() , and (180). For the second and third pairs, amplitudes are proportional to
, and (180). For the second and third pairs, amplitudes are proportional to ![]() , and (180). For all pairs, x-shifts depend on (181). The x-period of the first wave pair is
, and (180). For all pairs, x-shifts depend on (181). The x-period of the first wave pair is ![]() and the x-period of the second and third wave pairs is
and the x-period of the second and third wave pairs is ![]() that are defined by (182)-(183). If
that are defined by (182)-(183). If ![]() , the external wave oscillons (249) with the help of (108)-(109) and
, the external wave oscillons (249) with the help of (108)-(109) and
![]() (250)
(250)
are reduced to the doubled internal wave oscillons (234).
Like the external elementary oscillons (198), the external wave oscillons are neutral since on average they do not transfer any kinetic energy along the x-axis as
![]() (251)
(251)
Analogously, writing definitions (42) in y-eigenfunctions of external interaction ![]() with the help of (199) and (64) gives
with the help of (199) and (64) gives
![]()
![]() (252)
(252)
For any frozen ![]() , the first pair
, the first pair ![]() of external wave oscillons is transformed into at most 2-f neutral oscillons in y, which are produced by superpositions of two pairs of cosine waves
of external wave oscillons is transformed into at most 2-f neutral oscillons in y, which are produced by superpositions of two pairs of cosine waves ![]() and
and ![]() with wavenumbers
with wavenumbers ![]() , respectively. The second pair
, respectively. The second pair ![]() is reduced to 1-f neutral oscillons in y, which are formed by a superposition of sine waves
is reduced to 1-f neutral oscillons in y, which are formed by a superposition of sine waves ![]() with wavenumber
with wavenumber ![]() . The third pair
. The third pair ![]() is converted into at most 2-f neutral oscillons in y, which are generated by superpositions of two pairs of sine waves
is converted into at most 2-f neutral oscillons in y, which are generated by superpositions of two pairs of sine waves ![]() and
and ![]() with wavenumbers
with wavenumbers ![]() , correspondingly.
, correspondingly.
For the first and third pairs, amplitudes are proportional to ![]() , and (186). For the second pair, amplitudes depend on
, and (186). For the second pair, amplitudes depend on ![]() , and (186). For all pairs, y-shifts depend on (187). The y-period of the first and third wave pairs is
, and (186). For all pairs, y-shifts depend on (187). The y-period of the first and third wave pairs is ![]() and the y-period of the second wave pair is
and the y-period of the second wave pair is ![]() that are specified by (188)-(189). If
that are specified by (188)-(189). If ![]() , the external wave oscillons (252) are converted into the doubled internal wave oscillons (236).
, the external wave oscillons (252) are converted into the doubled internal wave oscillons (236).
Similar to the external elementary oscillons (200), the external wave oscillons do not transfer any kinetic energy along the y-axis because
![]() (253)
(253)
Using (64) and (201), we compute the external wave oscillons in the inhomogeneous Fourier expansion via the t-eigenfunctions of external interaction (117) as follows:
![]()
![]()
![]() (254)
(254)
For any frozen ![]() , the first pair
, the first pair ![]() of external wave oscillons is reduced to at most 4-f neutral oscillons in t, which are formed by superpositions of four sine waves
of external wave oscillons is reduced to at most 4-f neutral oscillons in t, which are formed by superpositions of four sine waves ![]() with frequencies
with frequencies ![]() correspondingly. The second pair
correspondingly. The second pair ![]() is transformed into at most 4-f neutral oscillons in t, which are generated by superpositions of four sine waves
is transformed into at most 4-f neutral oscillons in t, which are generated by superpositions of four sine waves ![]() with frequencies
with frequencies ![]() . The third pair
. The third pair ![]() is converted into at most 4-f neutral oscillons in t, which are produced by superpositions of four cosine waves
is converted into at most 4-f neutral oscillons in t, which are produced by superpositions of four cosine waves ![]() with frequencies
with frequencies ![]() , correspondingly.
, correspondingly.
For all pairs, amplitudes are proportional to ![]() , and (192) and t-shifts depend on (193). Temporal periods of all pairs are given by (202)-(204), respectively. If
, and (192) and t-shifts depend on (193). Temporal periods of all pairs are given by (202)-(204), respectively. If ![]() , the external wave oscillons (254) are transformed by (250), (127), and (171) into the doubled internal wave oscillons (238).
, the external wave oscillons (254) are transformed by (250), (127), and (171) into the doubled internal wave oscillons (238).
Because of (205) and (64),
![]() (255)
(255)
the external wave oscillons are also neutral in time since on average they do not transfer any kinetic energy.
The external wave oscillon ![]() with
with ![]() is shown in Figure 10 for independent parameters (95). Due to smallness of amplitudes
is shown in Figure 10 for independent parameters (95). Due to smallness of amplitudes ![]() compared with
compared with ![]() (248), the second pair
(248), the second pair ![]() coincide with a graph accuracy with 1-f neutral oscillons in x, which are formed by cosine waves
coincide with a graph accuracy with 1-f neutral oscillons in x, which are formed by cosine waves ![]() with wavenumber
with wavenumber ![]() , periods
, periods ![]() ,
, ![]() local x-maximums, and
local x-maximums, and ![]() local x-minimums, the numbers of which are specified by the magnitude of
local x-minimums, the numbers of which are specified by the magnitude of ![]() .
.
Along the y-axis, the second pair is reduced to 1-f neutral oscillons in y with periods ![]() . The second pair is displayed with a graph accuracy by 2-f neutral oscillons in t with frequencies
. The second pair is displayed with a graph accuracy by 2-f neutral oscillons in t with frequencies ![]() , periods
, periods ![]() ,
, ![]() local t-maximums, and
local t-maximums, and ![]() local t-minimums, the numbers of which are specified by the magnitude of
local t-minimums, the numbers of which are specified by the magnitude of ![]() .
.
5. Group Oscillons and Pulsons
5.1. The Group Oscillon of Propagation
In agreement with (53) and (206), the group oscillon of propagation of the velocity potential
![]() (256)
(256)
For any frozen ![]() , the group oscillon of propagation is represented by a M-f neutral oscillon in x that is formed by M wave oscillons of propagation, i.e. the superposition of sine waves with wavenumbers
, the group oscillon of propagation is represented by a M-f neutral oscillon in x that is formed by M wave oscillons of propagation, i.e. the superposition of sine waves with wavenumbers ![]() and parameters of (206) for
and parameters of (206) for ![]() .
.
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 10. The external wave oscillon Kw,a,2,c,3: (a)—Kw,a,2,c,3 (x) (249), (b)—Kw,a,2,c,3 (y) (252), (c)—Kw,a,2,c,3 (t) (254) for independent parameters (95).
An x-period of the group oscillon of propagation
![]() (257)
(257)
where ![]() is an integer and
is an integer and ![]() is given by (74) for all
is given by (74) for all ![]() .
.
Due to (53), (211), (257), the group oscillon of propagation is neutral in the x-direction since
![]() (258)
(258)
Similarly, we use (53) and (212) to find the group oscillon of propagation
![]() (259)
(259)
For any frozen ![]() , the group oscillon of propagation is displayed by a M-f neutral oscillon in y that is generated by M wave oscillons of propagation, i.e. the superposition of sine waves with wavenumbers
, the group oscillon of propagation is displayed by a M-f neutral oscillon in y that is generated by M wave oscillons of propagation, i.e. the superposition of sine waves with wavenumbers ![]() and parameters of (212) for
and parameters of (212) for ![]() .
.
A y-period of the group oscillon of propagation
![]() (260)
(260)
where ![]() is an integer and
is an integer and ![]() is provided by (82) for all
is provided by (82) for all ![]() .
.
Due to (53), (217), (260), the group oscillon of propagation is also neutral in the y-direction because
![]() (261)
(261)
Usage (53) and (218) yields
![]() (262)
(262)
For any frozen ![]() , the group oscillon of propagation is presented by a 2M-f neutral oscillon in t that is produced by M wave oscillons of propagation, i.e. the superposition of sine waves
, the group oscillon of propagation is presented by a 2M-f neutral oscillon in t that is produced by M wave oscillons of propagation, i.e. the superposition of sine waves ![]() with frequencies
with frequencies ![]() ,
, ![]() , and parameters of (218) for
, and parameters of (218) for ![]() .
.
A t-period of the group oscillon of propagation
![]() (263)
(263)
where ![]() is an integer and
is an integer and ![]() is specified by (93) for all
is specified by (93) for all ![]() .
.
Due to (53), (223), (263),
![]() (264)
(264)
The group oscillon of propagation of the velocity potential is neutral in time, as well.
The group oscillon of propagation ![]() with
with ![]() is shown in Figure 11 for independent parameters (95). The group oscillon of propagation is visualized as a 3-f neutral oscillon in x with period
is shown in Figure 11 for independent parameters (95). The group oscillon of propagation is visualized as a 3-f neutral oscillon in x with period ![]() , 14 local x-maximums, and 14 local x-minimums, the numbers of which do not exceed
, 14 local x-maximums, and 14 local x-minimums, the numbers of which do not exceed ![]() due to four merged x-maximums and x-minimums.
due to four merged x-maximums and x-minimums.
The group oscillon of propagation is depicted by a 3-f neutral oscillon in y with period ![]() , seven local y-maximums, and seven local y-minimums, the numbers of which do not exceed
, seven local y-maximums, and seven local y-minimums, the numbers of which do not exceed ![]() due to two merged y-maximums and y-minimums. The group oscillon of propagation is displayed in terms of a 6-f neutral oscillon in t with period
due to two merged y-maximums and y-minimums. The group oscillon of propagation is displayed in terms of a 6-f neutral oscillon in t with period ![]() , 10 local t-maximums, and 10 local t-minimums, the numbers of which do not exceed
, 10 local t-maximums, and 10 local t-minimums, the numbers of which do not exceed ![]() due to five merged t-maximums and t-minimums.
due to five merged t-maximums and t-minimums.
5.2. The Group Pulson of Propagation
Because of (56) and (132), the group pulson of propagation of the kinetic energy
![]() (265)
(265)
For any frozen ![]() , the group pulson of propagation is reduced to a 0-f supercritical pulson in x with an energy shift proportional to
, the group pulson of propagation is reduced to a 0-f supercritical pulson in x with an energy shift proportional to ![]() ,
, ![]() .
.
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 11. The group oscillon of propagation Kg,i,m: (a)—Kg,i,m (x) (256), (b)—Kg,i,m (y) (259), (c)—Kg,i,m (t) (262) for independent parameters (95).
In agreement with (56) and (135),
![]() (266)
(266)
The group pulson of propagation transfers a positive amount of the kinetic energy along the x-axis.
Using (56) and (138), we compute the group pulson of propagation as follows
![]() (267)
(267)
For any frozen ![]() , the group pulson of propagation is transformed into the 0-f supercritical pulson in y with the energy shift proportional to
, the group pulson of propagation is transformed into the 0-f supercritical pulson in y with the energy shift proportional to ![]() ,
, ![]() .
.
Because of (56) and (141), the group pulson of propagation also transfers the positive amount of the kinetic energy along the y-axis since
![]() (268)
(268)
Usage of (56) and (143)-(144) gives the group pulson of propagation in the following form:
![]() (269)
(269)
For any frozen ![]() , the group pulson of propagation is converted into the 0-f supercritical pulson in t with the energy shift proportional to
, the group pulson of propagation is converted into the 0-f supercritical pulson in t with the energy shift proportional to ![]() and (146).
and (146).
Due to (56) and (149),
![]() (270)
(270)
i.e. the group pulson of propagation transfers the positive amount of the kinetic energy in time, as well.
5.3. The Internal Group Oscillon
Combining (59) and (152) returns the inhomogeneous Fourier expansion of the internal group oscillon along the x-axis
![]() (271)
(271)
For any frozen ![]() , the internal group oscillon is converted into a 1-f nonneutral oscillon in x, which is formed by a superposition of sine waves
, the internal group oscillon is converted into a 1-f nonneutral oscillon in x, which is formed by a superposition of sine waves ![]() with wavenumber
with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to ![]() and (133), x-shifts (72), and an energy shift proportional to
and (133), x-shifts (72), and an energy shift proportional to ![]() and (153) except
and (153) except ![]() . The x-period of the internal group oscillon is specified by (134).
. The x-period of the internal group oscillon is specified by (134).
For the same reason as for the internal elementary oscillons,
![]() (272)
(272)
Integral (272) proves that the internal group oscillon on average is nonneutral as it transfers a kinetic energy along the x-axis.
Similarly, we use (59) and (165) to find the inhomogeneous Fourier expansion of the internal group oscillon along the y-axis
![]() (273)
(273)
For any frozen ![]() , the internal group oscillon is reduced to a 1-f nonneutral oscillon in y, which is produced by a superposition of sine waves
, the internal group oscillon is reduced to a 1-f nonneutral oscillon in y, which is produced by a superposition of sine waves ![]() with wavenumber
with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to ![]() and (139), y-shifts (81), and an energy shift proportional to
and (139), y-shifts (81), and an energy shift proportional to ![]() and (166) except
and (166) except ![]() . The y-period of the internal group oscillon is given by (140).
. The y-period of the internal group oscillon is given by (140).
Analogously to the internal elementary oscillons, the internal group oscillon on average is nonneutral as it also transfers a kinetic energy along the y-axis because
![]() (274)
(274)
Usage of (59) and (170) yields the inhomogeneous Fourier expansion of the internal group oscillon in time
![]() (275)
(275)
For any frozen ![]() , the internal group oscillon is transformed into a 2-f neutral oscillon in t, which is generated by a superposition of sine waves
, the internal group oscillon is transformed into a 2-f neutral oscillon in t, which is generated by a superposition of sine waves ![]() with frequencies
with frequencies ![]() , respectively, amplitudes proportional to
, respectively, amplitudes proportional to ![]() , and (145), and t-shifts depending on (91). The temporal period of the group oscillon
, and (145), and t-shifts depending on (91). The temporal period of the group oscillon ![]() is provided by (229).
is provided by (229).
The internal group oscillon on average is neutral as does not transfer in time any kinetic energy since
![]() (276)
(276)
The internal group oscillon ![]() with
with ![]() is shown in Figure 12 for independent parameters (95). The internal group oscillons
is shown in Figure 12 for independent parameters (95). The internal group oscillons ![]() are visualized by 1-f nonneutral oscillons in x with periods
are visualized by 1-f nonneutral oscillons in x with periods ![]() , in terms of 1-f nonneutral oscillons in y with periods
, in terms of 1-f nonneutral oscillons in y with periods ![]() , and via 2-f neutral oscillons in t with periods
, and via 2-f neutral oscillons in t with periods ![]() ,
, ![]() local t-maximums and
local t-maximums and ![]() local t-minimums, the numbers of which are specified by
local t-minimums, the numbers of which are specified by ![]()
5.4. The Diagonal Group Oscillon
Combining (62) and (179) yields the inhomogeneous Fourier expansion of the diagonal group oscillon along the x-axis
![]() (277)
(277)
For any frozen ![]() , the diagonal group oscillon is transformed into a 1-f neutral oscillon in x, which is generated by a superposition of two cosine waves
, the diagonal group oscillon is transformed into a 1-f neutral oscillon in x, which is generated by a superposition of two cosine waves ![]() with wavenumber
with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to ![]() and (180), and x-shifts depending on (181). The x-wavelength of the diagonal group oscillon is provided by
and (180), and x-shifts depending on (181). The x-wavelength of the diagonal group oscillon is provided by ![]() (183). If
(183). If ![]() , the diagonal group oscillon (277) by (108)-(109) is transformed into the doubled group pulson of propagation (265).
, the diagonal group oscillon (277) by (108)-(109) is transformed into the doubled group pulson of propagation (265).
The diagonal group oscillon on average also is neutral along the x-axis as
![]() (278)
(278)
Analogously, we combine (62) and (185) to find the inhomogeneous Fourier expansion of the diagonal group oscillon along the y-axis
![]() (279)
(279)
For any frozen ![]() , the diagonal group oscillon is reduced to a 1-f neutral oscillon in y, which is formed by a superposition of two cosine waves
, the diagonal group oscillon is reduced to a 1-f neutral oscillon in y, which is formed by a superposition of two cosine waves ![]() with wavenumber
with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to ![]() and (186), and y-shifts depending on (187). The y-wavelength of the diagonal group oscillon is specified by
and (186), and y-shifts depending on (187). The y-wavelength of the diagonal group oscillon is specified by ![]() (189). If
(189). If ![]() , the diagonal group oscillon (279) is reduced to the doubled group pulson of propagation (267).
, the diagonal group oscillon (279) is reduced to the doubled group pulson of propagation (267).
The diagonal group oscillon is also neutral along the y-axis since it does not transfer on average any kinetic energy because
![]() (280)
(280)
Application of (62) and (191) gives the inhomogeneous Fourier expansion of the diagonal group oscillon in time
![]() (281)
(281)
For any frozen ![]() , the diagonal group oscillon is converted into a 2-f neutral oscillon in t, which is produced by a superposition of cosine waves
, the diagonal group oscillon is converted into a 2-f neutral oscillon in t, which is produced by a superposition of cosine waves ![]() with frequencies
with frequencies ![]() correspondingly, amplitudes proportional to
correspondingly, amplitudes proportional to ![]() and (192), and t-shifts depending on (193). If
and (192), and t-shifts depending on (193). If ![]() , the diagonal group oscillon (281) is transformed into the doubled group pulson of propagation (269).
, the diagonal group oscillon (281) is transformed into the doubled group pulson of propagation (269).
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 12. The internal group oscillon Kg,i,3,j,3: (a)—Kg,i,3,j,3 (x) (271), (b)—Kg,i,3,j,3 (y) (273), (c)—Kg,i,3,j,3 (t) (275) for independent parameters (95).
A temporal period of the diagonal group oscillon
![]() (282)
(282)
where ![]() are integers and
are integers and ![]() are specified by (194).
are specified by (194).
Integral over the t-period of the diagonal group oscillon
![]() (283)
(283)
The diagonal group oscillon on average is neutral in time, as well, because it does not transfer any kinetic energy.
The diagonal group oscillon ![]() with
with ![]() is shown in Figure 13 for independent parameters (95). The diagonal group oscillons
is shown in Figure 13 for independent parameters (95). The diagonal group oscillons ![]() are displayed in terms of 1-f neutral oscillons in x with periods specified by the magnitude of
are displayed in terms of 1-f neutral oscillons in x with periods specified by the magnitude of ![]() , via 1-f neutral oscillons iny with periods indicated by the magnitude of
, via 1-f neutral oscillons iny with periods indicated by the magnitude of ![]() , and by 2-f neutral oscillons in t with periods
, and by 2-f neutral oscillons in t with periods ![]() ,
, ![]() local t-maximums and
local t-maximums and ![]() local t-minimums, the numbers of which are specified by the magnitude of
local t-minimums, the numbers of which are specified by the magnitude of ![]() .
.
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 13. The diagonal group oscillon Kg,i,2,i,3: (a)—Kg,i,2,i,3 (x) (277), (b)—Kg,i,2,i,3 (y) (279), (c)—Kg,i,2,i,3 (t) (281) for independent parameters (95).
5.5. The External Group Oscillon
Substituting (197) in (65), we recast definition (43) in the inhomogeneous Fourier expansion of the external group oscillon along the x-axis
![]() (284)
(284)
For any frozen ![]() , the external group oscillon is reduced to a 2-f neutral oscillon in x, which is generated by a superposition of four sine waves
, the external group oscillon is reduced to a 2-f neutral oscillon in x, which is generated by a superposition of four sine waves ![]() with wavenumber
with wavenumber ![]() and two cosine waves
and two cosine waves ![]() with wavenumber
with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to ![]() , and (180), and x-shifts depending on (181). The x-wavelength of the external group oscillon is specified by
, and (180), and x-shifts depending on (181). The x-wavelength of the external group oscillon is specified by ![]() (182)-(183). If
(182)-(183). If ![]() , the external group oscillon (284) is transformed by (108), (109), (250) into the doubled internal group oscillon (271).
, the external group oscillon (284) is transformed by (108), (109), (250) into the doubled internal group oscillon (271).
Like the external elementary oscillons, the external group oscillon on average does not transfer any kinetic energy along the x-axis as
![]() (285)
(285)
Similarly, writing definition (43) in y-eigenfunctions of external interaction ![]() with the help of (199) and (65) yields
with the help of (199) and (65) yields
![]() (286)
(286)
For any frozen ![]() , the external group oscillon is converted into a 2-f neutral oscillon in y, which is produced by a superposition of four sine waves
, the external group oscillon is converted into a 2-f neutral oscillon in y, which is produced by a superposition of four sine waves ![]() with wavenumber
with wavenumber ![]() and two cosine waves
and two cosine waves ![]() with wavenumber
with wavenumber ![]() , amplitudes proportional to
, amplitudes proportional to ![]() , and (186), and y-shifts depending on (187). The y-wavelength of the external group oscillon
, and (186), and y-shifts depending on (187). The y-wavelength of the external group oscillon ![]() is defined by (188)-(189). If
is defined by (188)-(189). If ![]() , the external group oscillon (286) is reduced to the doubled internal group oscillon (273).
, the external group oscillon (286) is reduced to the doubled internal group oscillon (273).
Because
![]() (287)
(287)
the external group oscillon on average does not transfer any kinetic energy along the y-axis, as well.
Substitution of (201) in (65) and collection of like terms produce the inhomogeneous Fourier expansion of the external group oscillon in time
![]() (288)
(288)
For any frozen ![]() , the external group oscillon is converted into at most sextet-frequency (6-f) neutral oscillon in t, which are formed by a superposition of four sine waves
, the external group oscillon is converted into at most sextet-frequency (6-f) neutral oscillon in t, which are formed by a superposition of four sine waves ![]() with frequencies
with frequencies ![]() and two cosine waves
and two cosine waves ![]() with frequencies
with frequencies ![]() , respectively, amplitudes proportional to
, respectively, amplitudes proportional to ![]() , and (192), and t-shifts depending on (193). If
, and (192), and t-shifts depending on (193). If ![]() , the external group oscillon (288) is transformed by (127) and (250) into the doubled internal group oscillon (275).
, the external group oscillon (288) is transformed by (127) and (250) into the doubled internal group oscillon (275).
A temporal period of the external group oscillon
![]() (289)
(289)
where ![]() is an integer and
is an integer and ![]() is specified by (194) for
is specified by (194) for ![]() .
.
The external group oscillon on average does not transfer in time any kinetic energy since
![]() (290)
(290)
The external group oscillon ![]() with
with ![]() is shown in Figure 14 for independent parameters (95). The external group oscillons
is shown in Figure 14 for independent parameters (95). The external group oscillons ![]() are visualized by 2-f neutral oscillons in x with periods
are visualized by 2-f neutral oscillons in x with periods ![]() ,
, ![]() local x-maximums, and
local x-maximums, and ![]() local x-minimums, the numbers of which are specified by
local x-minimums, the numbers of which are specified by ![]() .
.
The external group oscillons are depicted by 2-f neutral oscillons in y with periods ![]() ,
, ![]() local y-maximums, and
local y-maximums, and ![]() local y-minimums, the numbers of which do not exceed or equal to
local y-minimums, the numbers of which do not exceed or equal to ![]() due to
due to ![]() merged y-maximums and y-minimums.
merged y-maximums and y-minimums.
Because of smallness of amplitudes ![]() compared with
compared with ![]() (248) and repeated frequencies, the external group oscillons are displayed with a graph accuracy as 4-f neutral oscillons in t with periods
(248) and repeated frequencies, the external group oscillons are displayed with a graph accuracy as 4-f neutral oscillons in t with periods ![]() ,
, ![]() local t-maximums and
local t-maximums and ![]() local t-minimums, the numbers of which do not exceed or equal to
local t-minimums, the numbers of which do not exceed or equal to ![]() due to
due to ![]() merged t-maximums and t-minimums.
merged t-maximums and t-minimums.
6. Energy Oscillons and Pulsons
6.1. The Energy Pulson of Propagation
Due to (30) and (265), the cumulative energy of all group pulsons of propagation along the x-axis is given by the energy pulson of propagation
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 14. The external group oscillon Kg,i,2,j,3: (a)—Kg,i,2,j,3 (x) (284), (b)—Kg,i,2,j,3 (y) (286), (c)—Kg,i,2,j,3 (t) (288) for independent parameters (95).
![]() (291)
(291)
For any frozen ![]() , the energy pulson of propagation is formed by the superposition of M 0-f supercritical pulsons in x with energy shifts of (265).
, the energy pulson of propagation is formed by the superposition of M 0-f supercritical pulsons in x with energy shifts of (265).
A global x-period of internal interaction
![]() (292)
(292)
where ![]() is an integer and
is an integer and ![]() is specified by (134) for all
is specified by (134) for all ![]() .
.
The energy pulson of propagation transfers a positive amount of the kinetic energy along the x-axis as
![]() (293)
(293)
Because of (30) and (267), the cumulative energy of all group pulsons of propagation along the y-axis is also given by (291). For any frozen ![]() , the energy pulson of propagation is produced by the superposition of M 0-f supercritical pulsons in y with energy shifts of (267).
, the energy pulson of propagation is produced by the superposition of M 0-f supercritical pulsons in y with energy shifts of (267).
A global y-period of internal interaction
![]() (294)
(294)
where ![]() is an integer and
is an integer and ![]() is defined by (140) for all
is defined by (140) for all ![]() .
.
The energy pulson of propagation also transfers a positive amount of the kinetic energy along the y-axis since
![]() (295)
(295)
In the view of (30) and (269), the energy pulson of propagation in time is once more described by (291). For any frozen ![]() , the energy pulson of propagation is generated by the superposition of M 0-f supercritical pulsons in t with energy shifts of (269).
, the energy pulson of propagation is generated by the superposition of M 0-f supercritical pulsons in t with energy shifts of (269).
A global t-period of internal interaction
![]() (296)
(296)
where ![]() is an integer and
is an integer and ![]() is given by (229) for all
is given by (229) for all ![]() .
.
Because
![]() (297)
(297)
the energy pulson of propagation transfers a positive amount of the kinetic energy in time, as well.
6.2. The Internal Energy Oscillon
In agreement with (40) and (271), the cumulative energy of all internal group oscillons along the x-axis is described the internal energy oscillon
![]() (298)
(298)
For any frozen ![]() , the internal energy oscillon is represented by an M-f nonneutral oscillon in x that is generated by M internal group oscillons, i.e. the superposition of sine waves
, the internal energy oscillon is represented by an M-f nonneutral oscillon in x that is generated by M internal group oscillons, i.e. the superposition of sine waves ![]() for
for ![]() with wavenumbers
with wavenumbers ![]() , parameters of (271), and x-period (292).
, parameters of (271), and x-period (292).
Average of (298) over the global x-period of internal interaction
![]() (299)
(299)
due to (292), (272), and the additive interval property. The internal energy oscillon on average is nonneutral since it transfers the kinetic energy along the x-axis.
In the view of (40) and (273), the cumulative energy of all internal group oscillons along the y-axis is given the internal energy oscillon
![]() (300)
(300)
For any frozen ![]() , the internal energy oscillon is displayed by an M-f nonneutral oscillon in y, which is produced by M internal group oscillons, namely, the superposition of sine waves
, the internal energy oscillon is displayed by an M-f nonneutral oscillon in y, which is produced by M internal group oscillons, namely, the superposition of sine waves ![]() for
for ![]() with wavenumbers
with wavenumbers ![]() , parameters of (273), and y-period (294).
, parameters of (273), and y-period (294).
The internal energy oscillon on average is also nonneutral along the y-axis because it transfers the kinetic energy as average of (300) over the global y-period (294)
![]() (301)
(301)
Because of (40) and (275), the internal energy oscillon takes the following t-form:
![]() (302)
(302)
For any frozen ![]() , the internal energy oscillon is at most 2M-f neutral oscillon in t, which is formed by M internal group oscillons, viz. the superposition of sine waves
, the internal energy oscillon is at most 2M-f neutral oscillon in t, which is formed by M internal group oscillons, viz. the superposition of sine waves ![]() and
and ![]() with frequencies
with frequencies ![]() and
and ![]() , respectively, parameters of (275), and t-period (296).
, respectively, parameters of (275), and t-period (296).
Integral of (302) over the global t-period of internal interaction
![]() (303)
(303)
shows that ![]() on average does not transfer in time any kinetic energy.
on average does not transfer in time any kinetic energy.
The internal energy oscillon ![]() with
with ![]() is shown in Figure 15 for independent parameters (95).
is shown in Figure 15 for independent parameters (95). ![]() is displayed by a 3-f nonneutral oscillon in x with 18 local x-maximums and 18 local x-minimums, the numbers of which are specified by
is displayed by a 3-f nonneutral oscillon in x with 18 local x-maximums and 18 local x-minimums, the numbers of which are specified by ![]() .
. ![]() is depicted as a 3-f nonneutral oscillon in y with nine local y-maximums and nine local y-minimums, the numbers of which are given by
is depicted as a 3-f nonneutral oscillon in y with nine local y-maximums and nine local y-minimums, the numbers of which are given by ![]() . Due to the repeated frequency
. Due to the repeated frequency ![]() ,
, ![]() is visualized by a 5-f neutral oscillon in t with nine local t-maximums, and nine local t-minimums, the number of which are specified by
is visualized by a 5-f neutral oscillon in t with nine local t-maximums, and nine local t-minimums, the number of which are specified by ![]() , where
, where ![]() are multipliers of
are multipliers of ![]() (147) in
(147) in ![]() for
for ![]() .
.
6.3. The Diagonal Energy Oscillon
Due to (35) and (277), a cumulative energy of all diagonal group oscillons along the x-axis is expressed via the diagonal energy oscillon
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 15. The internal energy oscillon Ke,i,m,j,m: (a)—Ke,i,m,j,m (x) (298), (b)—Ke,i,m,j,m (y) (300), (c)—Ke,i,m,j,m (t) (302) for independent parameters (95).
![]() (304)
(304)
with a global x-period of diagonal interaction
![]() (305)
(305)
where ![]() is an integer and
is an integer and ![]() is specified by (183) for all
is specified by (183) for all ![]() .
.
For any frozen ![]() , the diagonal energy oscillon is transformed into at most M(M-1)/2-f neutral oscillon in x that is formed by
, the diagonal energy oscillon is transformed into at most M(M-1)/2-f neutral oscillon in x that is formed by ![]() diagonal group oscillons, i.e. the superposition of cosine waves
diagonal group oscillons, i.e. the superposition of cosine waves ![]() with wavenumber
with wavenumber ![]() for
for ![]() ,
, ![]() , and parameters of (277).
, and parameters of (277).
Because integral of (304) over the global x-period of diagonal interaction
![]() (306)
(306)
the diagonal energy oscillon on average does not transfer any kinetic energy along the x-axis.
In agreement with (35) and (279), a cumulative energy of all diagonal group oscillons along the y-axis is described by the diagonal energy oscillon
![]() (307)
(307)
with a global y-period of diagonal interaction
![]() (308)
(308)
where ![]() is an integer and
is an integer and ![]() is defined by (189) for all
is defined by (189) for all ![]() .
.
For any frozen ![]() , the diagonal energy oscillon is converted into at most M(M-1)/2-f neutral oscillon in y that is generated by
, the diagonal energy oscillon is converted into at most M(M-1)/2-f neutral oscillon in y that is generated by ![]() diagonal group oscillons, viz. the superposition of cosine waves
diagonal group oscillons, viz. the superposition of cosine waves ![]() with wavenumber
with wavenumber ![]() for
for ![]() ,
, ![]() , and parameters of (279).
, and parameters of (279).
The diagonal energy oscillon on average also does not transfer any kinetic energy along the y-axis since
![]() (309)
(309)
Because of (35) and (281), the diagonal energy oscillon takes the following t-form:
![]() (310)
(310)
with a global t-period of diagonal interaction
![]() (311)
(311)
where ![]() is an integer and
is an integer and ![]() is given by (282) for all
is given by (282) for all ![]() .
.
For any frozen ![]() , the diagonal energy oscillon is reduced to at most M(M-1)-f neutral oscillon in t, which is produced by
, the diagonal energy oscillon is reduced to at most M(M-1)-f neutral oscillon in t, which is produced by ![]() diagonal group oscillons, specifically, the superposition of cosine waves
diagonal group oscillons, specifically, the superposition of cosine waves ![]() with frequencies
with frequencies ![]() for
for ![]() ,
, ![]() , respectively, and parameters of (281).
, respectively, and parameters of (281).
Since
![]() (312)
(312)
the diagonal energy oscillon on average does not transfer any kinetic energy in time, as well.
The diagonal energy oscillon ![]() with
with ![]() is shown in Figure 16 for independent parameters (95).
is shown in Figure 16 for independent parameters (95). ![]() is represented by a 3-f neutral oscillon in x with three local x-maximums and three local x-minimums, the numbers of which are specified by the magnitude of
is represented by a 3-f neutral oscillon in x with three local x-maximums and three local x-minimums, the numbers of which are specified by the magnitude of ![]() .
. ![]() is displayed as a 3-f neutral oscillon in y with three local y-maximums and three local y-minimums, the numbers of which do not exceed the magnitude of
is displayed as a 3-f neutral oscillon in y with three local y-maximums and three local y-minimums, the numbers of which do not exceed the magnitude of ![]() due to a single merged y-maximum and y-minimum. As the frequencies
due to a single merged y-maximum and y-minimum. As the frequencies ![]() are repeated,
are repeated, ![]() is visualized via a 4-f neutral oscillon with nine local t-maximums and nine local t-minimums, the numbers of which do not exceed the magnitude of
is visualized via a 4-f neutral oscillon with nine local t-maximums and nine local t-minimums, the numbers of which do not exceed the magnitude of ![]() due to a single merged t-maximum and t-minimum, where
due to a single merged t-maximum and t-minimum, where ![]() are multipliers of
are multipliers of ![]() (194) in
(194) in ![]() for
for ![]() .
.
6.4. The External Energy Oscillon
Combining (45) and (284), we find the cumulative energy of all external group oscillons along the x-axis that is given by the external energy oscillon
![]() (313)
(313)
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 16. The diagonal energy oscillon Ke,i,m,i,n: (a)—Ke,i,m,i,n (x) (304), (b)—Ke,i,m,i,n (y) (307), (c)—Ke,i,m,i,n (t) (310) for independent parameters (95).
with a global x-period of external interaction
![]() (314)
(314)
where ![]() is an integer and
is an integer and ![]() is provided by (182)-(183) for all
is provided by (182)-(183) for all ![]() .
.
For any frozen ![]() , the external energy oscillon is transformed into at most M(M-1)-f neutral oscillon in x that is formed by
, the external energy oscillon is transformed into at most M(M-1)-f neutral oscillon in x that is formed by ![]() external group oscillons, i.e. the superposition of sine waves
external group oscillons, i.e. the superposition of sine waves ![]() with wavenumber
with wavenumber ![]() and cosine waves
and cosine waves ![]() with wavenumber
with wavenumber ![]() for
for ![]() ,
, ![]() , and parameters of (284).
, and parameters of (284).
Because
![]() (315)
(315)
the external energy oscillon on average does not transfer any kinetic energy along the x-axis.
In the view of (45) and (286), the external energy oscillon along the y-axis takes the following y-form:
![]() (316)
(316)
with a global y-period of external interaction
![]() (317)
(317)
where ![]() is an integer and
is an integer and ![]() is defined by (188)-(189) for all
is defined by (188)-(189) for all ![]() .
.
For any frozen ![]() , the external energy oscillon is converted into at most M(M-1)-f neutral oscillon in y, which is produced by
, the external energy oscillon is converted into at most M(M-1)-f neutral oscillon in y, which is produced by ![]() external group oscillons, namely, the superposition of sine waves
external group oscillons, namely, the superposition of sine waves ![]() with wavenumber
with wavenumber ![]() and cosine waves
and cosine waves ![]() with wavenumber
with wavenumber ![]() for
for ![]() ,
, ![]() , and parameters of (286).
, and parameters of (286).
The external energy oscillon is also neutral along the y-axis since
![]() (318)
(318)
We use (45) and (288) to compute the inhomogeneous Fourier expansion the external energy oscillon in time
![]() (319)
(319)
with a global t-period of external interaction
![]() (320)
(320)
where ![]() is an integer and
is an integer and ![]() is specified by (289) for all
is specified by (289) for all ![]() .
.
For any frozen ![]() the external energy oscillon is transformed into at most 3M (M − 1)-f neutral oscillon in t, which is generated by
the external energy oscillon is transformed into at most 3M (M − 1)-f neutral oscillon in t, which is generated by ![]() external group oscillon, viz. the superposition of sine waves
external group oscillon, viz. the superposition of sine waves ![]() with frequencies
with frequencies ![]() and cosine waves
and cosine waves ![]() with frequencies
with frequencies ![]() , for
, for ![]() ,
, ![]() , respectively, and parameters of (288).
, respectively, and parameters of (288).
For the reason that
![]() (321)
(321)
the external energy oscillon on average does not transfer any kinetic energy in time, as well.
The external energy oscillon ![]() with
with ![]() is shown in Figure 17 for independent parameters (95).
is shown in Figure 17 for independent parameters (95). ![]() is displayed by a 6-f neutral oscillon in x with 26 local x-maximums and 26 local x-minimums, the numbers of which are specified by
is displayed by a 6-f neutral oscillon in x with 26 local x-maximums and 26 local x-minimums, the numbers of which are specified by ![]() , where
, where ![]() are multipliers of
are multipliers of ![]() (183) in
(183) in ![]() for
for ![]() .
. ![]() is visualized by a 6-f neutral oscillon in y with six local y-maximums and six local y-minimums, the numbers of which are specified by
is visualized by a 6-f neutral oscillon in y with six local y-maximums and six local y-minimums, the numbers of which are specified by ![]() , where
, where ![]() are multipliers of
are multipliers of ![]() (189) in
(189) in ![]() for
for ![]() .
.
Due to repeated frequencies ![]() ,
, ![]() is represented via a 15-f neutral oscillon with 16 local t-maximums and 16 local t-minimums, the numbers of which do not exceed
is represented via a 15-f neutral oscillon with 16 local t-maximums and 16 local t-minimums, the numbers of which do not exceed ![]() due to a single merged t-maximum and t-minimum, where
due to a single merged t-maximum and t-minimum, where ![]() are multipliers of
are multipliers of ![]() (194) in
(194) in ![]() for
for ![]() .
.
6.5. The Cumulative Energy Pulson
We then use (66), (291), (298), (304), and (313), to find the inhomogeneous Fourier expansion of the cumulative pulson of the kinetic energy along the x-axis
![]() (322)
(322)
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 17. The external energy oscillon Ke,i,m,j,n: (a)—Ke,i,m,j,n (x) (313), (b)—Ke,i,m,j,n (y) (316), (c)—Ke,i,m,j,n (t) (319) for independent parameters (95).
where ![]() is the constant density,
is the constant density, ![]() are the wave numbers in the
are the wave numbers in the ![]() directions,
directions, ![]() are functional amplitudes of the 3-d DSK functions (48),
are functional amplitudes of the 3-d DSK functions (48), ![]() are trigonometric amplitudes (68),
are trigonometric amplitudes (68), ![]() is energy shift (109),
is energy shift (109), ![]() are sine waves (109) with wavenumber
are sine waves (109) with wavenumber ![]() ,
, ![]() are nonlinear amplitudes (246),
are nonlinear amplitudes (246), ![]() are cosine waves (101) with wavenumber
are cosine waves (101) with wavenumber ![]() , and
, and ![]() are sine waves (101) with wavenumber
are sine waves (101) with wavenumber ![]() .
.
For any frozen ![]() , the cumulative energy pulson is converted to at most M 2-f supercritical pulson in x, which is formed by the superposition of the energy pulson of propagation
, the cumulative energy pulson is converted to at most M 2-f supercritical pulson in x, which is formed by the superposition of the energy pulson of propagation ![]() , the internal energy oscillon
, the internal energy oscillon ![]() , the diagonal energy oscillon
, the diagonal energy oscillon ![]() , and the external energy oscillon
, and the external energy oscillon ![]() . The total number of various wavenumbers is at most
. The total number of various wavenumbers is at most ![]() since there are M wave numbers
since there are M wave numbers ![]() and
and ![]() wavenumbers
wavenumbers ![]() .
.
A global x-wavelength of the cumulative energy pulson
![]() (323)
(323)
where ![]() are integers,
are integers, ![]() is the global x-period of internal interaction (292),
is the global x-period of internal interaction (292), ![]() is the global x-period of diagonal interaction (305), and
is the global x-period of diagonal interaction (305), and ![]() is the global x-period of external interaction (314).
is the global x-period of external interaction (314).
Combining (323), (292), (305), and (314) yields the global x-wavelength of ![]()
![]() (324)
(324)
where ![]() are integers,
are integers, ![]() (134) is the local x-period of internal interaction for
(134) is the local x-period of internal interaction for ![]() ,
, ![]() and
and ![]() (183) are the local x-periods of external interaction for
(183) are the local x-periods of external interaction for ![]() ,
, ![]() .
.
The cumulative energy pulson on average transfer a positive amount of the kinetic energy along the x-axis since
![]() (325)
(325)
in the view of (66), (293), (299), (306), (315), (323), and the additive interval property.
Combining (66), (291), (300), (307), and (316) yields the inhomogeneous Fourier expansion of the cumulative energy pulson along the y-axis
![]() (326)
(326)
where ![]() are trigonometric amplitudes (77),
are trigonometric amplitudes (77), ![]() is the energy shift,
is the energy shift, ![]() are the sine waves with wavenumber
are the sine waves with wavenumber ![]() ,
, ![]() are the cosine waves with wavenumber
are the cosine waves with wavenumber ![]() , and
, and ![]() are the sine waves with wavenumber
are the sine waves with wavenumber ![]() .
.
For any frozen ![]() , the cumulative energy pulson is transformed into at most M 2-f supercritical pulson in y, which is generated by the superposition of
, the cumulative energy pulson is transformed into at most M 2-f supercritical pulson in y, which is generated by the superposition of ![]() . The total number of various wavenumbers is at most
. The total number of various wavenumbers is at most ![]() since there are M wavenumbers
since there are M wavenumbers ![]() and
and ![]() wavenumbers
wavenumbers ![]() .
.
A global y-wavelength of the cumulative energy pulson
![]() (327)
(327)
where ![]() are integers,
are integers, ![]() is the global y-period of internal interaction (294),
is the global y-period of internal interaction (294), ![]() is the global y-period of diagonal interaction (308), and
is the global y-period of diagonal interaction (308), and ![]() is the global y-period of external interaction (317).
is the global y-period of external interaction (317).
We then use (327), (294), (308), and (317) to compute the global y-wavelength of ![]()
![]() (328)
(328)
where ![]() are integers,
are integers, ![]() (140) is the local y-period of internal interaction for
(140) is the local y-period of internal interaction for ![]() ,
, ![]() and
and ![]() (189) are the local y-periods of external interaction for
(189) are the local y-periods of external interaction for ![]() ,
, ![]() .
.
The cumulative energy pulson on average also transfer a positive amount of the kinetic energy along the y-axis because
![]() (329)
(329)
due to (66), (295), (301), (309), (318), (327), and the additive interval property.
Usage of (66), (291), (302), (310), and (319) gives the inhomogeneous Fourier expansion of the cumulative energy in time
![]() (330)
(330)
where ![]() are trigonometric amplitudes (87),
are trigonometric amplitudes (87), ![]() are sine waves (126) with frequencies
are sine waves (126) with frequencies ![]() , respectively,
, respectively, ![]() are cosine waves (117) with frequencies
are cosine waves (117) with frequencies ![]() , and
, and ![]() are sine waves (117) with frequencies
are sine waves (117) with frequencies ![]() , correspondingly.
, correspondingly.
For any frozen ![]() , the cumulative energy pulson is reduced to at most 2M (2M − 1)-f supercritical pulson in t, which is produced by the superposition of
, the cumulative energy pulson is reduced to at most 2M (2M − 1)-f supercritical pulson in t, which is produced by the superposition of ![]() . The total number of various frequencies is at most
. The total number of various frequencies is at most ![]() because there are M frequencies
because there are M frequencies ![]() and
and ![]() frequencies
frequencies ![]() for
for ![]() .
.
A global t-wavelength of the cumulative energy pulson
![]() (331)
(331)
where ![]() are integers,
are integers, ![]() is the global t-period of internal interaction (296),
is the global t-period of internal interaction (296), ![]() is the global t-period of diagonal interaction (311), and
is the global t-period of diagonal interaction (311), and ![]() is the global t-period of external interaction (320).
is the global t-period of external interaction (320).
Using (331), (296), (311), and (320) returns the global t-wavelength of ![]()
![]() (332)
(332)
where ![]() are integers,
are integers, ![]() (147) are the local t-periods of internal interaction for
(147) are the local t-periods of internal interaction for ![]() ,
, ![]() ,
, ![]() (194) are the local t-periods of external interaction for
(194) are the local t-periods of external interaction for ![]() ,
, ![]() ,
, ![]() .
.
In agreement with (66), (297), (303), (312), (321), (331), and the additive interval property,
![]() (333)
(333)
Indeed, the cumulative energy pulson remains positive for all ![]() despite numerous oscillons of internal and external interaction, which locally may transfer negative amounts of the kinetic energy.
despite numerous oscillons of internal and external interaction, which locally may transfer negative amounts of the kinetic energy.
The cumulative energy pulson ![]() with
with ![]() is shown in Figure 18 for independent parameters (95).
is shown in Figure 18 for independent parameters (95). ![]() is visualized by a 9-f supercritical pulson in x with 23 local x-maximums and 23 local x-minimums, the numbers of which do not exceed
is visualized by a 9-f supercritical pulson in x with 23 local x-maximums and 23 local x-minimums, the numbers of which do not exceed ![]() due to 13 merged x-maximums and x-minimums. By the reason of repeated frequencies
due to 13 merged x-maximums and x-minimums. By the reason of repeated frequencies ![]() ,
, ![]() is depicted by a 7-f supercritical pulson in y with six local y-maximums and six local y-minimums, the numbers of which do not exceed
is depicted by a 7-f supercritical pulson in y with six local y-maximums and six local y-minimums, the numbers of which do not exceed ![]() due to three merged y-maximums and y-minimums.
due to three merged y-maximums and y-minimums.
Because of smallness of amplitudes ![]() compared with
compared with ![]() (248) and repeated frequencies
(248) and repeated frequencies ![]() ,
, ![]() is displayed with a graph accuracy as a 19-f supercritical pulson with 15 local t-maximums and 15 local t-minimums, the numbers of which do not exceed
is displayed with a graph accuracy as a 19-f supercritical pulson with 15 local t-maximums and 15 local t-minimums, the numbers of which do not exceed ![]() due to three merged t-maximums and t-minimums.
due to three merged t-maximums and t-minimums.
7. Discussion
The elementary pulsons of propagation, the internal elementary oscillons, the diagonal elementary oscillons, and the external elementary oscillons describe various scalar interactions between the scalar fields ![]() of the velocity potential of the elementary oscillons of propagation. The wave pulsons of propagation, the internal wave oscillons, the diagonal wave oscillons, and the external wave oscillons express different vector interactions between the velocity fields of wave groups
of the velocity potential of the elementary oscillons of propagation. The wave pulsons of propagation, the internal wave oscillons, the diagonal wave oscillons, and the external wave oscillons express different vector interactions between the velocity fields of wave groups ![]() . Superpositions of the various vector interactions with frozen
. Superpositions of the various vector interactions with frozen ![]() and
and ![]() are represented by the group pulsons of propagation, the internal group oscillons, the diagonal group oscillons, and the external group oscillons. Summation of the group pulsons of propagation, the internal group oscillons, the diagonal group oscillons, and the external group oscillons with respect to all
are represented by the group pulsons of propagation, the internal group oscillons, the diagonal group oscillons, and the external group oscillons. Summation of the group pulsons of propagation, the internal group oscillons, the diagonal group oscillons, and the external group oscillons with respect to all ![]() and
and ![]() results in the energy pulson of propagation, the internal energy oscillon, the diagonal energy oscillon, and the external energy oscillon. The superposition of the energy pulson of propagation, the internal energy oscillon, the diagonal energy oscillon, and the external energy oscillon generates the cumulative energy pulson.
results in the energy pulson of propagation, the internal energy oscillon, the diagonal energy oscillon, and the external energy oscillon. The superposition of the energy pulson of propagation, the internal energy oscillon, the diagonal energy oscillon, and the external energy oscillon generates the cumulative energy pulson.
![]()
Figure 18. The cumulative energy pulson Ke: (a)—Ke (x) (322), (b)—Ke (y) (326), (c)—Ke (t) (330) for independent parameters (95).
Classification of various types of pulsons and oscillons, which are decomposed in the inhomogeneous Fourier expansion, is considered in Section 3.5. The nested structure of the deterministic quantization of the kinetic energy of deterministic chaos of the elementary pulsons of propagation, the internal, diagonal, and external elementary oscillons, the wave pulsons of propagation, the internal, diagonal, and external wave oscillons, the group pulsons of propagation, the internal, diagonal, and external group oscillons, the energy pulsons of propagation, the internal, diagonal, and external energy oscillons, and the cumulative energy pulson is considered in Section 2.7. The nested structure of the deterministic quantization resembles the nested structure of objects of quantum mechanics: elementary particles, atoms, molecules, etc. This resemblance correlates with the quantum-like properties of the scalar and vector kinematic structures that are considered in [3]: the scalar-vector duality, the quadrality of the theoretical DSK and DVK structures, and the equiprobability the experimental DSK and DVK structures.
Amplitudes of the wave pulsons and oscillons are larger than amplitudes of the elementary pulsons and oscillons, amplitudes of the group pulsons and oscillons exceed amplitudes of the wave pulsons and oscillons, amplitudes of the energy pulsons and oscillons surpass amplitudes of the group pulsons and oscillons, and amplitudes of the cumulative energy pulson go above amplitudes of the energy pulsons and oscillons. Consequently, the elementary, wave, group, and energy pulsons and oscillons constitute also nested structures in amplitudes.
The x-, y-, t-periods of the wave pulsons and oscillons are larger or equal to the x-, y-, t-periods of the elementary pulsons and oscillons. Similarly, the x-, y-, t-periods of the group pulsons and oscillons exceed or equal to the x-, y-, t-periods of the wave pulsons and oscillons. Analogously, the x-, y-, t-periods of the energy pulsons and oscillons surpass or equal to the x-, y-, t-periods of the group pulsons and oscillons. Eventually, the x-, y-, t-periods of the cumulative energy pulson go beyond or equal to the x-, y-, t-periods of the energy pulsons and oscillons. Therefore, the elementary, wave, group, and energy pulsons and oscillons constitute nested structures with respect to the x-, y-, t-periods, as well.
Topology of the elementary pulson of propagation, the wave pulson of propagation, and the cumulative energy pulson in Figure 2, Figure 7, and Figure 18, respectively, is the same as of the solitons on shallow water, the solitary waves on shallow water with uniform [4] and linear [5] vorticity, the solitary waves generated by crossed electric and magnetic fields [6], and the pulsatory waves of the Korteweg-de Vries equation [7]. Topology of the diagonal elementary oscillon, the external elementary oscillon, the diagonal wave oscillon, the external wave oscillon, the diagonal group oscillon, the external group oscillon, the diagonal energy oscillon, and the external energy oscillon in Figure 4, Figure 5, Figure 9, Figure 10, Figure 13, Figure 14, Figure 16, and Figure 17, correspondingly, resembles the topology of nonlinear waves and solitons on deep water [8].
Pulsatory and oscillatory structure of the wave pulsons and oscillons is less complicated than the structure of the elementary pulsons and oscillons. Pulsatory and oscillatory structure of the group pulsons and oscillons is also less sophisticated than the structure of the wave pulsons and oscillons. This simplification is produced by compensation of undulations of complementary structures caused by the Pythagorean resonance, i.e. the Pythagorean identity. Oscillatory structure of the energy oscillons is more complex than the structure of the group oscillons due to a substantial growth in number of independent wavenumbers and frequencies.
Since chaos of physical systems could be explained by superposing a large number of deterministic solutions [9], it looks interesting to explore the effect of independent parameters on the rate of chaotization of the exact solution for deterministic chaos [3]. It also looks appealing to consider the Lagrangian and the Eulerian properties of the elementary, wave, group, energy pulsons and oscillons in the view of various types of wave lattices [2].
Acknowledgements
The support of CAAM and the College of Mount Saint Vincent is gratefully acknowledged.