Using Riccati Equation to Construct New Solitary Solutions of Nonlinear Difference Differential Equations ()
1. Introduction
The study of solitary waves and solitons is a frontier topic at present. From hydrodynamics, optics, plasma, condensed matter physics to basic particle physics, and even astrophysics and biology, it is everywhere [1] - [6]. We all found that there are experimental facts or physical mechanisms for the existence of solitons. Most of the laws of physics can establish mathematical models under certain conditions, and many studies of nonlinear identification can be attributed to the NLEEs finally. Therefore, finding their exact solutions, such as breathing solutions and solitary wave solutions, is of great significance for exploring related nonlinear problems, and it is also an important focus of mathematical and physical research. Great progress has been made in recent centuries. Many powerful and effective methods have been proposed in the literature to obtain the exact solution of the NLEEs. For example, tanh-sech method and the extended tanh-coth method [7] [8], F-expansion method [9] [10], Jacobi elliptic function expansion method [11] [12], auxiliary equation method [13] [14] [15], and so on.
In Ref. [16], by using the Riccati equation
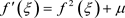(1)
the following solitary wave solutions are obtained
, (
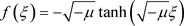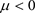) (2)
, (
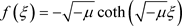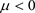) (3)
This method is powerful and effective, and can be applied to solve constant coefficient, variable coefficient and high-dimensional NLEEs. In this paper, we consider to the Riccati equation in the following form
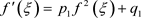(4)
Equation (4) has the following hyperbolic function solution
, (
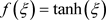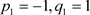) (5)
, (
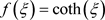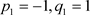) (6)
A new auxiliary function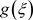 
is introduced, which satisfies the following relationship
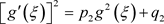(7)
Equation (7) has the following hyperbolic function solution
, (
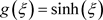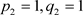) (8)
, (
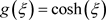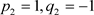) (9)
Suppose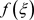 
and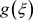 
have the following formal solution
![]()
(10)
Substituting Equation (10) into Equation (4) and using Equation (7), we have
![]()
, (![]()
) (11)
![]()
, (![]()
) (12)
It is obvious ![]()
is also the solution of Equation (4) in the condition of![]()
. Equation (5) and Equation (6) are a pair of solutions satisfying this condition. So we also have
![]()
, (![]()
) (13)
![]()
, (![]()
) (14)
again suppose ![]()
and ![]()
have the following formal solution
![]()
(15)
where r is constant to be determined. We have
![]()
, (![]()
) (16)
![]()
, (![]()
) (17)
Equations (16) and (17) are the new types of solitary wave solutions, which are rarely found in the other documents. Then using the auxiliary Equation (4) and its solutions (5), (6) and (11)-(17), the solving process of NLEEs is greatly simplified.
The frame work of the paper is as follows: Section 2 introduces the method of solving the (2 + 1)-dimensional NLEEs. Section 3 establishes how to operate this method for producing new solitary wave solutions of (2 + 1)-dimensional BLMP equation and (2 + 1)-dimensional KDV equation. Section 4 is the conclusion.
2. Method
The following the (2 + 1)-dimensional NLEE is considered
![]()
(18)
It is assumed that Equation (18) has the following traveling wave solution
![]()
,![]()
(19)
where ω is a wave parameter to be determined. Substitute Equation (19) into Equation (18), and Equation (18) becomes the following ordinary differential equation
![]()
(20)
where u' means du/dξ. Suppose Equation (18) has the following formal solution
![]()
(21)
where ai are constants determined later. The positive integer n can be controlled by controlling the homogeneous balance between the governing nonlinear term and the highest order derivative of u(ξ) in Equation (20). f(ξ) is determined by Equation (4). Substituting Equation (4) and Equation (21) into (20), and setting the coefficients of fi(ξ) to zero, then solving the resulting equations the solitary wave solutions of Equation (20) can be obtained.
3. Application of the Method
3.1. (2 + 1)-Dimensional BLMP Equation
The following (2 + 1)-dimensional BLMP equation [17] [18] is considered
![]()
(22)
As a (2 + 1) dimensional model, Equation (22) has been applied to the interaction between Riemann waves along the Y axis and long waves along the X axis. Substituting Equation (19) into Equation (22), integrating once and setting the integration constant to zero yields
![]()
(23)
By the homogeneous balance between ![]()
and ![]()
in Equation (23), ![]()
can be obtained. So the solution of Equation (23) can be expressed as
![]()
(24)
substituting (24) into (23) yields a set of algebraic equations for a0, a1 and ω. Collecting all terms with the same power of f(ξ) together, equating each coefficient to zero. Then Solving the algebraic equations, a0, a1, and ω can be obtained as follows
![]()
,![]()
,![]()
(25)
By selecting different values of p1 and q1 the solitary wave solutions of (2 + 1)-dimensional BLMP equation can be obtained
Case 1 ![]()
(26)
where![]()
,![]()
.
Case 2 ![]()
(27)
where![]()
,![]()
.
Case 3 ![]()
(28)
where![]()
,![]()
.
Case 4 ![]()
(29)
where![]()
,![]()
.
Case 5 ![]()
(30)
where![]()
,![]()
.
Case 6 ![]()
(31)
where![]()
,![]()
.
Case 7 ![]()
(32)
where![]()
,![]()
.
Case 8 ![]()
(33)
where![]()
,![]()
.
These five types of solitary wave solutions of (2 + 1)-dimensional BLMP equation are shown as Figure 1, where C = t = 0. It can be seen in Figure 1 that all the figures show the kink type solitary waves with the spatial position. However, there are singularities in the solitary waves in Figure 1(b), Figure 1(c2), Figure 1(d1) and Figure 1(d2) owing to ![]()
or ![]()
at some spatial positions. Figure 1(f) shows a relatively flat solitary wave, which has rarely been found in previous studies.
![]()
![]()
Figure 1. Solitary waves of (2 + 1)-dimensional BLMP equation at C = t = 0. (a) Equation (26), (b) Equation (27), (c1) Equation (28) with + and (c2) Equation (28) with −, (d1) Equation (29) with + and (d2) Equation (29) with −, (e) Equation (32), (f) Equation (33).
3.2. (2 + 1)-Dimensional KDV Equation
Then we consider to reveal the new periodic wave and solitary solutions for the (2 + 1)-dimensional KDV equation [19] [20]
![]()
(34)
![]()
(35)
Substituting Equation (19) into Equation (34) and Equation (35) and integrating the above two equation once and setting the integration constant in Equation (35) to zero yields
![]()
(36)
![]()
(37)
According to homogeneous balance between ![]()
and ![]()
in Equation (36), ![]()
can be obtained. So the solution of Equation (31) can be expressed as
![]()
(38)
Following the method in Section 3.1, we can get
case 1![]()
,![]()
, ![]()
,![]()
(39)
case 2![]()
,![]()
, ![]()
,![]()
(40)
These two sets of solutions are the same type of solitary wave solutions, so we will only demonstrate case 2 below.
By selecting different values of p1 and q1 the solitary wave solutions of (2 + 1)-dimensional KDV equation can be obtained
Case 1 ![]()
(41)
where![]()
,![]()
.
Case 2 ![]()
(42)
where![]()
,![]()
.
Case 3 ![]()
(43)
where![]()
,![]()
.
Case 4 ![]()
(44)
where![]()
,![]()
.
Case 5 ![]()
(45)
where![]()
,![]()
.
Case 6 ![]()
(46)
where![]()
,![]()
.
Case 7 ![]()
(47)
where![]()
,![]()
.
Case 8 ![]()
(48)
where![]()
,![]()
.
These five types of solitary wave solutions of (2 + 1)-dimensional KDV equation are shown as Figure 2, where C = t = 0. As shown in Figure 2 all the figures show the bell type solitary waves with the spatial position. There are still singularities in the solitary waves in Figure 2(b), Figure 2(c2), Figure 2(d1) and Figure 2(d2) owing to wing to ![]()
or ![]()
at some spatial positions. A more pronounced flat solitary wave is shown in Figure 2(f).
![]()
![]()
Figure 2. Solitary waves of (2 + 1)-dimensional KDV equation at C = t = 0. (a) Equation (41), (b) Equation (42), (c1) Equation (43) with + and (c2) Equation (43) with −, (d1) Equation (44) with + and (d2) Equation (44) with −, (e) Equation (47), (f) Equation (48).
4. Conclusion
In this paper, we use Riccati equation to explore the solitary solution of the (2 + 1)-dimensional BLMP equation and (2 + 1)-dimensional KDV equation. Through two types of new function transformation Equation (7) and Equation (10), the Riccati equation is solved, and many new solitary wave solutions are obtained. With the cooperation of Equations (24) and (38), we have constructed abundant and new solitary wave solutions for the (2 + 1)-dimensional BLMP equation and (2 + 1)-dimensional KDV equation. The solitary wave solutions expressed by Equations (32), (33), (47) and (48) are rarely found in other documents, especially the solitary waves represented by Equations (33) and (48) shown in Figure 1(f) and Figure 2(f). This method can greatly simplify the calculation process, especially suitable for solving complex NLEEs. In the next work, we will use it to solve more complex nonlinear systems. It is simple and powerful mathematical tools and is promising for constructing abundant solitary solutions and can serve as a useful guide for a broad class of nonlinear problems in the study of mathematics and physics.