Invariance of the Electromagnetic Field Vectors Obtained in Course of the Lorentz Transformation Characteristic for the Relativistic Theory

S. Olszewski

Institute of Physical Chemistry, Polish Academy of Sciences, Warsaw, Poland.

DOI: 10.4236/jmp.2022.134028                

Abstract

The invariance of several new component electromagnetic-field vectors with respect to the Lorentz transformation has been demonstrated in the paper. The formalism of the classical relativistic mechanics has been applied in examining both the time-square variable of the field, as well as the square-values of the position coordinates of a moving particle.

Keywords

Lorentz Transformation, Electromagnetic Field Vectors

1. Introduction

The aim of the paper is to demonstrate the invariance of some new components of the electromagnetic field with respect to the Lorentz transformation characteristic for the special relativity. Well-known results of this kind were obtained a time ago for the mechanical parameters (see e.g. [1] ). In more recent calculations—see [2], the invariance of the difference of two coordinate squares, say the time t, and one of the Cartesian coordinates of position, say x, has been found:

$t^2-x^2={t^{\prime }}^2-{x^{\prime }}^2$ (1)

The parameters t and x entering (1) have been coupled by the Lorentz transformation giving $t^{\prime }$ and $x^{\prime }$ :

$t^{\prime }=\frac{t-\nu x}{\sqrt{1-{\nu }^2}}$ (2)

and

$x^{\prime }=\frac{x-\nu t}{\sqrt{1-{\nu }^2}}.$ (3)

Here

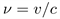(3a)

where is the actual velocity of the system directed along the coordinate x and c is a speed of light. The properties of the other coordinate transformations are

$y=y^{\prime }$ (4)

and

$z=z^{\prime }.$ (5)

In the present paper a special interest can be attributed to the electric and magnetic vector fields, viz.

$E\text{and}H$ (6)

and their Lorentz transformations. A list of such transformations is given in [3].

Perhaps the best known results concerning $E$ and $H$ are [3]:

$EH=\text{invariant}\mathrm{,}$ (7)

$H^2-E^2=\text{invariant}\mathrm{.}$ (8)

The aim of the paper is approached in two steps. In the first one—a less accurate one—we identify the variables t and x examined in [2] with some special components of the electromagnetic fields.

Another, more accurate calculation, makes a reference of the electromagnetic field vector components submitted to the motion without a reference to t and x; see Section 3. In this case only two pairs of field components submitted to the motion are examined.

2. New Invariant Relations Presented for the Vectors E and H

Relations in [3] being similar to (4) and (5) are:

$E_x={E^{\prime }}_x\mathrm{,}$ (9)

$H_x={H^{\prime }}_x\mathrm{.}$ (10)

When (9) and (10) are combined with (4) and (5), we obtain

$E_x\to {E^{\prime }}_x=y\to y^{\prime },$ (11)

$H_x\to {H^{\prime }}_x=z\to z^{\prime }.$ (12)

In the next step (see in ( [3], Section 23)) we can put

$x^{\prime }=H_y,$ (13)

$x={H^{\prime }}_y,$ (14)

$t^{\prime }=E_z,$ (15)

$t={E^{\prime }}_z,$ (16)

and examine transitions

$t\to t^{\prime }\mathrm{,}$ (17)

$x\to x^{\prime }\mathrm{.}$ (18)

Other identifications can be

${H^{\prime }}_y=t,$ (19)

${E^{\prime }}_z=x,$ (20)

$H_y=t^{\prime },$ (21)

$E_z=x^{\prime }.$ (22)

A combination of the Equations (13)-(16) leads to the difference

$\begin{array}{c}{t^{\prime }}^2-{x^{\prime }}^2=E_z^2-H_y^2={\left(\frac{t-\nu x}{\sqrt{1-{\nu }^2}}\right)}^2-{\left(\frac{x-\nu t}{\sqrt{1-{\nu }^2}}\right)}^2\\ =\frac{{\left({E^{\prime }}_z-\nu {H^{\prime }}_y\right)}^2}{1-{\nu }^2}-\frac{{\left({H^{\prime }}_y-\nu {E^{\prime }}_z\right)}^2}{1-{\nu }^2}\\ =\frac{1}{1-{\nu }^2}\left[{E^{\prime }}_z^2-2{E^{\prime }}_z{H^{\prime }}_y\nu +{\nu }^2{H^{\prime }}_y^2-{H^{\prime }}_y^2+2{E^{\prime }}_z{H^{\prime }}_y\nu -{\nu }^2{E^{\prime }}_z^2\right]\\ =\frac{1}{1-{\nu }^2}\left[\left(1-{\nu }^2\right){E^{\prime }}_z^2-\left(1-{\nu }^2\right){H^{\prime }}_y^2\right]\\ ={E^{\prime }}_z^2-{H^{\prime }}_y^2=t^2-x^2.\end{array}$ (23)

A similar calculation can be done on the basis of (19) - (22):

$\begin{array}{c}{t^{\prime }}^2-{x^{\prime }}^2=H_y^2-E_z^2={\left(\frac{t-\nu x}{\sqrt{1-{\nu }^2}}\right)}^2-{\left(\frac{x-\nu t}{\sqrt{1-{\nu }^2}}\right)}^2\\ =\frac{1}{1-{\nu }^2}\left[{\left({H^{\prime }}_y-\nu {E^{\prime }}_z\right)}^2-{\left({E^{\prime }}_z-\nu {H^{\prime }}_y\right)}^2\right]\\ =\frac{1}{1-{\nu }^2}\left[{H^{\prime }}_y^2-2{H^{\prime }}_y{E^{\prime }}_z\nu +{\nu }^2{E^{\prime }}_z^2-{E^{\prime }}_z^2+2{E^{\prime }}_z{H^{\prime }}_y\nu -{\nu }^2{H^{\prime }}_y^2\right]\\ =\frac{1}{1-{\nu }^2}\left[\left(1-{\nu }^2\right){H^{\prime }}_y^2-\left(1-{\nu }^2\right){E^{\prime }}_z^2\right]\\ ={H^{\prime }}_y^2-{E^{\prime }}_z^2=t^2-x^2.\end{array}$ (24)

In effect beyond of (7) and (8) we obtained two pairs of the electromagnetic field vectors which remain invariant upon the action of the Lorentz transformations:

1) ${t^{\prime }}^2-{x^{\prime }}^2=E_z^2-H_y^2={E^{\prime }}_z^2-{H^{\prime }}_y^2=t^2-x^2$ (25)

and

2) ${t^{\prime }}^2-{x^{\prime }}^2=H_y^2-E_z^2={H^{\prime }}_y^2-{E^{\prime }}_z^2=t^2-x^2.$ (26)

3. Two Components of the Electromagnetic Field Vectors Taken to Calculations

Expressions (25) and (26) can be considered only as an approximate result because the dimensions of ${t^{\prime }}^2,{x^{\prime }}^2$ or $t^2\mathrm{,}{x}^2$ differ from dimensions of ${E^{\prime }}_z^2\mathrm{,}{H^{\prime }}_y^2\mathrm{,}{E}_z^2\mathrm{,}{H}_y^2$ of the field counterparts. In order to get precise results we take into account the field components entering (25) and (26).

On the basis of [3], Section 23 we have

$E_y=\frac{{E^{\prime }}_y+\nu {H^{\prime }}_z}{{\left(1-{\nu }^2\right)}^{1/2}},$ (27)

$H_y=\frac{{H^{\prime }}_y-\nu {E^{\prime }}_z}{{\left(1-{\nu }^2\right)}^{1/2}},$ (28)

$E_z=\frac{{E^{\prime }}_z-\nu {H^{\prime }}_y}{{\left(1-{\nu }^2\right)}^{1/2}},$ (29)

$H_z=\frac{{H^{\prime }}_z+\nu {E^{\prime }}_y}{{\left(1-{\nu }^2\right)}^{1/2}}$ (30)

On that basis because of (9) and (10) we obtain

$\begin{array}{c}{E}^2-H^2=E_y^2+E_z^2-H_y^2-H_z^2\\ =\left({E^{\prime }}_y^2+2\nu {E^{\prime }}_y{H^{\prime }}_z+{\nu }^2{H^{\prime }}_z^2+{E^{\prime }}_z^2-2\nu {H^{\prime }}_y{E^{\prime }}_z+{\nu }^2{H^{\prime }}_y^2\right)\frac{1}{1-{\nu }^2}\\ -\left({H^{\prime }}_y^2-2\nu {H^{\prime }}_y{E^{\prime }}_z+{\nu }^2{E^{\prime }}_z^2+{H^{\prime }}_z^2+2\nu {H^{\prime }}_z{E^{\prime }}_y+{\nu }^2{E^{\prime }}_y^2\right)\frac{1}{1-{\nu }^2}\\ =\left({E^{\prime }}_y^2+{E^{\prime }}_z^2+{\nu }^2{H^{\prime }}_z^2+{\nu }^2{H^{\prime }}_y^2-{H^{\prime }}_y^2-{H^{\prime }}_z^2-{\nu }^2{E^{\prime }}_z^2-{\nu }^2{E^{\prime }}_y^2\right)\frac{1}{1-{\nu }^2}\\ ={E^{\prime }}_y^2+{E^{\prime }}_z^2-{H^{\prime }}_y^2-{H^{\prime }}_z^2.\end{array}$ (31)

This result-together with (9) and (10) proves the invariance of the difference

$E^2-H^2$ (32)

upon the Lorentz transformation.

Acknowledgements

The paper is dedicated to the memory of blessed Pier-Georgio Frassati suddenly deceased in Italy in 1925.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Sommerfeld, A. (1949) Mechanik. 4th Edition, Akademische Verlagsgesellschaft, Leipzig.
[2]	Susskind, L. and Friedeman, A. (2019) Special Theory of Relativity and Field Theory. Pruszynski Media, Warsaw (in Polish).
[3]	Landau, L.D. and Lifshits E.M. (1948) Field Theory. 2nd Edition. OGIZ, Moscow (in Russian).