An Explicit Formula of the Dirichlet-to-Neumann Map for a Radial Potential in Dimension 3

Fagueye Ndiaye

Laboratory of Mathematics of Decision and Numerical Analysis, Cheikh Anta Diop University, Dakar, Senegal.

DOI: 10.4236/jamp.2022.102030                

Abstract

In this paper, we provide an explicit expression for the full Dirichlet-to-Neumann map corresponding to a radial potential for the Schrödinger equation in 3-dimensional. We numerically implement the coefficients of the explicit formulas. In this work, Lipschitz type stability is established near the edge of the domain with giving estimation constant. That is necessary for the reconstruction of the potential from Dirichlet-to-Neuman map.

Keywords

Calderón’s Problem, Schrödinger Operator, Potential, Inverse Potential Problem, Dirichlet-to-Neuman Map, Numerical Simulations, Lipschitz Stability

1. Introduction

Let us consider a bounded domain $\Omega \subset {ℝ}^3$ with smooth boundary, the boundary value problem for the Schrödinger equation in $\Omega$ is given as follows

$\{\begin{array}{l}\left(-\Delta +q\right)u=0\text{in}\Omega \mathrm{,}\\ u=f\text{on}\partial \Omega \mathrm{.}\end{array}$ (1)

The boundary value is assumed to be in $H^{1/2}\left(\partial \Omega \right)$, and the potential q is real-valued function satisfying $q\in {\text{L}}^{\infty }\left(\Omega \right)$.

The inverse problem for the Schrödinger equation is related to Calderón’s problem (see [1] [2] [3] ). The inverse problem for the Schrödinger equation is to determine the potential function q from the measurements of $\frac{\partial u}{\partial \nu }$ for all possible functions f on the boundary of $\Omega$. That is the knowledge of the map, called also Dirichlet-to-Neumann map for the Schrödinger equation that associates to any $f\in H^{1/2}\left(\partial \Omega \right)$ the normal derivative, $\frac{\partial u}{\partial \nu }\in H^{-1/2}\left(\partial \Omega \right)$, of the unique solution of 1.

In the literature, the spectral geometry of the Dirichlet-to-Neumann map is a new and rapidly developing branch of spectral theory (see [4] and references therein). The eigenvalue problem for the Dirichlet-to-Neumann map, called the Steklov problems, was first introduced by V. A. Steklov more than a century ago. The geometric properties of Steklov eigenvalues and eigenfunctions have only recently begun to be explored. In [5], A. Rüland presented her recent work on Carleman estimates and quantitative unique continuation for solutions of fractional Schrödinger equations. As an application, she has obtained an upper bound on the vanishing order of the eigenfunctions and on the size of the nodal set. Her work is closely related to the results of Bellova and Lin in [6], Zelditch in [7] and Zhu in [8], since the Dirichlet-to-Neumann map could be viewed as a special case of a fractional Schrödinger operator. In [9], Akhmetgaliyev etal. were interested by computational method for extremal Steklov eigenvalue problems and applied it to study the problem of maximizing the p^th Steklov eigenvalue as a function of the domain with a volume constraint. Among other things, they reach the conjecture that the domain maximizing the p^th Steklov is unique, has the p-fold symmetry, and has at least one axis of symmetry.

Other studies to determine a map related to the Schrödinger operator in quantum mechanics and to estimate the entropy numbers of the function space have also developed. In [10], Dhahbi et al. used a new approach, the supersymmetric quantum mechanical (SUSY QM) formalism along with the shape invariance condition, and took into account the recent results from non-Hermitian quantum mechanics, to construct the quantum kinetic energy operator (KEO) within the Schrödinger operator in order to build a new class of exactly solvable models with position varying mass and exhibiting a harmonic-oscillator-like spectrum. In [11], Chen et al. discussed the entropy number of diagonal operator. On the one hand, they were interested in the order of entropy number of the finite dimensional diagonal operator. On the other hand, the order of entropy number of a class of infinite dimensional diagonal operators.

Other authors have been interested in Dirichlet-to-Neuman map in order to study the inverse problem of determining the potential for Schrödinger problem.

In [12], Greenleal et al. considered the Dirichlet-to-Neuman map associated to the Schrödinger equation with potential in a bounded Lipschitz domain in three or more dimensions, and showed that the integral of the potential over a two-plane is determined by the Cauchy data certain exponentially growing solutions on any neighborhood of the intersection of the two-plane with the boundary. In [13], Imanuvilov et al., in the 2-dimensional case, given a Dirichlet-to-Neuman map on a sub-boundary, proved the uniqueness of the determination of the potential under the assumption of the choice of the function space where the potential belongs. In [14], the authors considered the Schrödinger operator with a one-step radial potential q on a disk and the $\Lambda$ map which associates to q the corresponding Dirichlet-to-Neuman map ${\Lambda }_q$. They provide some numerical and analytical results on the range of the $\Lambda$ map and its stability for q. They based their study on a similar case, see [15], where the relationship between piecewise constant radial conductivities and the eigenvalues of the Dirichlet-to-Neuman map is known by an appropriate recurrence formula.

Our contribution in this paper is to determine an explicit formula for the Dirichlet to Neumann map for a piecewise constant radial potential in dimension three in a ball. Lipschitz type stability is established near the edge of the domain by giving estimation constant.

The paper is organized as follows. In Section 2, we define the Dirichlet to Neumann map for the Schrödinger equation, and then present the radial solutions of this equation in Section 3. In Section 4, we give an explicit formula for Dirichlet to Neumann map when the potential is radial, followed by some simulations. In Section 4, we study the stability of the map that associates a Dirichlet to Neumann map to any potential. In Section 5, we present conclusions and perspectives.

Our motivation of this paper is to know the Dirichlet-to-Neumann map ${\Lambda }_q$ for a piecewise constant radial potential q in dimension three in a ball from the knowledge of the Cauchy data $\left(f\mathrm{,}\frac{\partial u}{\partial \nu }\right)$ in order to be able to solve the inverse Schrödinger problem. Good knowledge of the characteristic properties of the Dirichlet-to-Neumann map ${\Lambda }_q$ allows solving the inverse problem which consists to determine the potential q from the knowledge of $\left(f\mathrm{,}{\Lambda }_q\right)$. And the study of this inverse problem also motivated us to study the Lipschitz type stability which will allow us to obtain a result at least at the edge of $\Omega$ with an estimate constant to be determined.

2. Definition of the Dirichlet-to-Neuman Map for the Schrödinger Equation

In this section we define the Dirichlet-to-Neuman map ${\Lambda }_q$ for the Schrödinger equation formally as

$\begin{array}{l}{\Lambda }_q\mathrm{<mo>\; :\; </mo>}{H}^{1/2}\left(\partial \Omega \right)\to H^{-1/2}\left(\partial \Omega \right)\\ f\mapsto {\Lambda }_q\left(f\right)={\frac{\partial u}{\partial \nu }|}_{\partial \Omega }\mathrm{,}\end{array}$ (2)

where $\nu$ is the outer unit normal vector to $\partial \Omega$.

The map $f\mapsto {\Lambda }_q\left(f\right)$ depends linearly on f. ${\Lambda }_q$ encodes the measurements of $\frac{\partial u}{\partial \nu }$ for all possible functions f on the boundary of $\Omega$.

We need to assume that 0 is not a Dirichlet eigenvalue of $\left(-\Delta +q\right)$ in $\Omega$.

Now, we look more closely at the direct problem with the potential. Let the unit ball B in ${ℝ}^3$ be defined by $B=\left\{x\in {ℝ}^3\mathrm{<mo>\; :\; </mo>}\left|x\right|\le 1\right\}$.

We focus on $q\in {\text{L}}^{\infty }\left(B\right)$ with $q\left(x\right)=q\left(\left|x\right|\right)$ is radial, $f\in H^{\frac{1}{2}}\left(\partial B\right)$ given and assuming that 0 is not an eigenvalue of

$\{\begin{array}{l}\left(-\Delta +q\right)u=0\text{in}\left|x\right|<\mathrm{1,}\\ u=f\text{on}\left|x\right|=1.\end{array}$ (3)

These choices guarantee the existence of a solution of (3) by the Fourier method and 0 is not an eigenvalue ensuring the uniqueness of the solution.

Then the map $f\mapsto {\Lambda }_q\left(f\right)$ is well defined. To obtain an explicit formula for the Dirichlet-to-Neuman map ${\Lambda }_q$ defined in (2), we will consider the following results (see [15] ):

1) If $q\left(x\right)\ne 0$ then ${\Lambda }_q$ is diagonalisable in the sense that the spectrum is discrete, $\left\{{\lambda }_k\left[q\right]\mathrm{,}k\in {\mathbb{N}}_0\right\}$.

In this case, if ${\mathcal{N}}_k$ is the subspace of spherical harmonics of degree k, then

${{\Lambda }_q|}_{{\mathcal{N}}_k}={\lambda }_k\left[q\right]I_{{\mathcal{N}}_k}.$

2) If $q\left(x\right)=0$ and ${\varphi }_k\in {\mathcal{N}}_k$ then ${\Lambda }_0\left({\varphi }_k\right)=k{\varphi }_k,k=0,1,2,\cdots$

3) ${\lambda }_k\left[q\right]-k\to 0$ if $k\to \infty$.

Then in the following, we give a recurrence relation for the explicit calculation of the spectrum in the case where $q\left(x\right)$ is a step potential, to give an approximation of the spectrum of a general potential. For this, we need to introduce some properties that will be useful.

3. Radial Solutions

In this section, we present some results obtained from writing problem (3) in polar coordinates $r>0,\theta \in {\mathbb{S}}^2$. We want to obtain “complex geometrical optics” solutions or solutions of Faddeev types, see [16].

Lemma 3.1: If u is the solution of (3) and $v\left(r\mathrm{,}\theta \right)=u\left(r\theta \right)$ in terms of spherical harmonics, then the function v satisfies the problem

$\{\begin{array}{l}{r}^2{v}^{″}+2r{v}^{\prime }+{\Delta }_{S}v-q\left(r\right)r^{2}v=0,\\ \underset{r>0,r\to 0}{\lim }v\left(r,\theta \right)<\infty ,v\left(1,\theta \right)=f\left(\theta \right).\end{array}$ (4)

where $-{\Delta }_S{Y}_{\mathcal{l}}^k=\mathcal{l}\left(\mathcal{l}+1\right)Y_{\mathcal{l}}^k$, $Y_{\mathcal{l}}^k\in {\mathcal{N}}_{\mathcal{l}}$.

Proof Lemma 3.1: In spherical coordinates, the Laplacien is given by

$\Delta =\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial }{\partial r}\right)+\frac{1}{r^2\sin \alpha }\frac{\partial }{\partial \alpha }\left(\sin \alpha \frac{\partial }{\partial \alpha }\right)+\frac{1}{r^2{\sin }^2\alpha }\frac{{\partial }^2}{\partial {\varphi }^2},$

Or

$\Delta =\frac{{\partial }^2}{\partial r^2}+\frac{2}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}{\Delta }_S,$

where

${\Delta }_S=\frac{1}{\sin \alpha }\frac{\partial }{\partial \alpha }\left(\sin \alpha \frac{\partial }{\partial \alpha }\right)+\frac{1}{{\sin }^2\alpha }\frac{{\partial }^2}{\partial {\varphi }^2}.$

Then

$\left(-\Delta +q\right)v=0$

is equivalent to

$-\frac{{\partial }^{2}v}{\partial r^2}-\frac{2}{r}\frac{\partial v}{\partial r}-\frac{1}{r^2}{\Delta }_{S}v+q\left(r\right)v=0.$

Or

$r^2\frac{{\partial }^{2}v}{\partial r^2}+2r\frac{\partial v}{\partial r}+{\Delta }_{S}v-q\left(r\right)v{r}^2=0.$

As the solution must be finite at the origin then we have the following condition

$\underset{r>0,r\to 0}{\lim }v\left(r,\theta \right)<\infty ,$

In addition, we have $r=1$ in ${\mathbb{S}}^2$. Then the Dirichlet condition is equivalent to $v\left(1,\theta \right)=f\left(\theta \right)$ where f depends only of $\theta \in {\mathbb{S}}^2$. $\square$

Lemma 3.2: If $f\left(\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{f}_{\mathcal{l}k}{Y}_{\mathcal{l}}^k\left(\theta \right)$ in $H^{1/2}\left({\mathbb{S}}^2\right)$ , then the equation (3) admits a unique solution of the form

$v\left(r,\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{v}_{\mathcal{l}k}\left(r\right)Y_{\mathcal{l}}^k\left(\theta \right),$ (5)

where $v_{\mathcal{l}k}$ satisfies the problem

$\{\begin{array}{l}{r}^2{v^{″}}_{\mathcal{l}k}+2r{v^{\prime }}_{\mathcal{l}k}-\mathcal{l}\left(\mathcal{l}+1\right)v_{\mathcal{l}k}-q\left(r\right)r^2{v}_{\mathcal{l}k}=0,r\in \left(0,1\right),\\ \underset{r>0,r\to 0}{\lim }{v}_{\mathcal{l}k}\left(r\right)<\infty ,v_{\mathcal{l}k}\left(1\right)=f_{\mathcal{l}k}.\end{array}$ (6)

Proof Lemma 3.2: We know, that problem (3) admits a unique solution $v\left(r\mathrm{,}\theta \right)$ with $r>0$ and $\theta \in {\mathbb{S}}^2$, following Section 2.

If $f\left(\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{f}_{\mathcal{l}k}{Y}_{\mathcal{l}}^k\left(\theta \right)$ then we can write $v\left(1,\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{f}_{\mathcal{l}k}{Y}_{\mathcal{l}}^k\left(\theta \right)$.

Using the separation of variables $v\left(r,\theta \right)=v\left(r\right)g\left(\theta \right)$, the completeness property of the spherical harmonics implies that any well-behaved function g of $\theta \in {\mathbb{S}}^2$, that is which is single valued, continuous and finite, can be written as

$g\left(\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{a}_{\mathcal{l}k}{Y}_{\mathcal{l}}^k\left(\theta \right)$, $\theta \in {\mathbb{S}}^2$ for some choice of coefficients $a_{\mathcal{l}k}$.

Choosing $a_{\mathcal{l}k}=1$, then we have $g\left(\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{Y}_{\mathcal{l}}^k\left(\theta \right)$, $\theta \in {\mathbb{S}}^2$. Taking $r=1$ in $v\left(r,\theta \right)=v\left(r\right)g\left(\theta \right)$, we obtain $v\left(1,\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{v}_{\mathcal{l}k}\left(1\right)Y_{\mathcal{l}}^k\left(\theta \right)$ and then, $v_{\mathcal{l}k}\left(1\right)=f_{\mathcal{l}k}$ in ${\mathbb{S}}^2$.

From $v\in H^1\left(\overline{B\left(\mathrm{0,1}\right)}\right)$, we obtain $v\left(r,\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{v}_{\mathcal{l}k}\left(r\right)Y_{\mathcal{l}}^k\left(\theta \right)$. Since $v\left(r,\theta \right)$ satisfies (3) then, we have

$\begin{array}{l}{\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{r}^2\frac{{\partial }^2{v}_{\mathcal{l}k}\left(r\right)}{\partial r^2}{Y}_{\mathcal{l}}^k\left(\theta \right)+{\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}2r\frac{\partial v_{\mathcal{l}k}\left(r\right)}{\partial r}{Y}_{\mathcal{l}}^k\left(\theta \right)\\ +{\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{v}_{\mathcal{l}k}\left(r\right){\Delta }_S{Y}_{\mathcal{l}}^k\left(\theta \right)-{\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}q\left(r\right)r^2{v}_{\mathcal{l}k}\left(r\right)Y_{\mathcal{l}}^k\left(\theta \right)=0.\end{array}$

with ${\Delta }_S=\frac{1}{\sin \alpha }\frac{\partial }{\partial \alpha }\left(\sin \alpha \frac{\partial }{\partial \alpha }\right)+\frac{1}{{\sin }^2\alpha }\frac{{\alpha }^2}{\partial {\varphi }^2}$, where $\theta =\left(\alpha \mathrm{,}\varphi \right)\in {\mathbb{S}}^2$.

Since $-{\Delta }_S{Y}_{\mathcal{l}}^k=\mathcal{l}\left(\mathcal{l}+1\right)Y_{\mathcal{l}}^k$, we have

${\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}\left(r^2\frac{{\partial }^2{v}_{\mathcal{l}k}\left(r\right)}{\partial r^2}+2r\frac{\partial v_{\mathcal{l}k}\left(r\right)}{\partial r}-\mathcal{l}\left(\mathcal{l}+1\right)v_{\mathcal{l}k}\left(r\right)-q\left(r\right)r^2{v}_{\mathcal{l}k}\left(r\right)\right)Y_{\mathcal{l}}^k\left(\theta \right)=0.$

We know ${\left\{Y_{\mathcal{l}}^k\right\}}_{\mathcal{l}=0,1,2,\cdots ;k=-\mathcal{l},-\mathcal{l}+1,\cdots ,\mathcal{l}-1,\mathcal{l}}$ is an orthonormal basis, then $v_{\mathcal{l}k}\left(r\right)$ verifies (6).

Lemma 3.3: If $v_{\mathcal{l}k}$ is the solution of (6), then we have

${\Lambda }_q\left(f\right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{v^{\prime }}_{\mathcal{l}k}\left(1\right)Y_{\mathcal{l}}^k\left(\theta \right).$ (7)

Proof Lemma 3.3: We know for all $f\in H^{1/2}\left({\mathbb{S}}^2\right)$, ${\Lambda }_q\left(f\right)={\frac{\partial v}{\partial r}|}_{{\mathbb{S}}^2}$ where v is the unique solution of (3).

Using lemma (3.2), we have

$\begin{array}{l}\frac{\partial v}{\partial r}={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}\frac{\partial v_{\mathcal{l}k}}{\partial r}{Y}_{\mathcal{l}}^k\left(\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{v^{\prime }}_{\mathcal{l}k}{Y}_{\mathcal{l}}^k\left(\theta \right),\\ \text{for}\text{all}r>0,\theta \in {\mathbb{S}}^2\end{array}$.

Then ${\frac{\partial v}{\partial r}|}_{{\mathbb{S}}^2}={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{v^{\prime }}_{\mathcal{l}k}\left(1\right)Y_{\mathcal{l}}^k\left(\theta \right)$, $r=1$ and $\theta \in {\mathbb{S}}^2$. $\square$

We note that the differential equation in (6) does not depend on k, so we will eliminate the dependence on k. Then

Lemma 3.4: If in (6) we take $f=Y_{\mathcal{l}}$ , that is, the spherical harmonic of degree $\mathcal{l}$ , it follows that

${\Lambda }_q\left(Y_{\mathcal{l}}\right)\left(\theta \right)={v^{\prime }}_{\mathcal{l}}\left(1\right)Y_{\mathcal{l}}\left(\theta \right).$ (8)

Then ${v^{\prime }}_l\left(1\right)$ is an eigenvalue of ${\Lambda }_q$ with multiplicity $2\mathcal{l}+1$ and its eigenfunctions are ${\left\{Y_{\mathcal{l}}^k\right\}}_{k=-\mathcal{l},-\mathcal{l}+1,\cdots ,\mathcal{l}-1,\mathcal{l}}$ .

Proof Lemma 3.4: If $f=Y_{\mathcal{l}}$, then from (3.2) $v\left(r\mathrm{,}\theta \right)=v_{\mathcal{l}}\left(r\right)Y_{\mathcal{l}}$.

It follows that from (3.3), ${\frac{\partial v}{\partial r}|}_{{\mathbb{S}}^2}={v^{\prime }}_{\mathcal{l}}\left(1\right)Y_{\mathcal{l}}\left(\theta \right)$ and ${\Lambda }_q\left(Y_{\mathcal{l}}\right)\left(\theta \right)={v^{\prime }}_{\mathcal{l}}\left(1\right)Y_{\mathcal{l}}\left(\theta \right)$.

According to [15], ${v^{\prime }}_{\mathcal{l}}\left(1\right)$ is an eigenvalue of ${\Lambda }_q$ with multiplicity $2\mathcal{l}+1$ and its eigenfunctions are ${\left\{Y_{\mathcal{l}}^k\right\}}_{k=-\mathcal{l},-\mathcal{l}+1,\cdots ,\mathcal{l}-1,\mathcal{l}}$.

In the next section, we will use these results to give an explicit formula for the DN map when the potential is a radial function.

4. Explicit Formula for the Dirichlet to Neumann Map

4.1. The Case Where q Is a Piecewise Constant Radial Potential

Let us introduce the theorem where the expression of the Dirichlet-to-Neuman map is presented when q is a piecewise constant radial potential, based on the results of the previous section.

In the following, for all $\mathcal{l}\in \mathbb{N}$, $p_{\mathcal{l}}^m\left(r\right)$ denotes the Bessel function of the first type $j_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)$ or the Bessel function of the second type $i_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)$, and $q_{\mathcal{l}}^m\left(r\right)$ denotes the modified Bessel function of the first type $y_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)$ or the modified Bessel function of the second type ${\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)$.

Theorem 4.1: Let the unit ball B in ${ℝ}^3$ and the scaled potential $q\in {\text{L}}^{\infty }\left(B\right)$ with

$q\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m{\chi }_{\left(r_{m-1},r_m\right)},r=\left|x\right|,$ (9)

where $n\ge 1$ , ${\gamma }_m\mathrm{,}{r}_m\in ℝ$ ,with $m=1,2,\cdots ,n$ and $0=r_0<r_1<\cdots <r_{n-1}<r_n=1$ ,such that the Dirichlet problem for $-\Delta +q$ is well-posed.

Then there is an explicit formula for the Dirichlet-to-Neumann map defined as follows:

$\begin{array}{l}{\Lambda }_q\left(Y_{\mathcal{l}}^k\left(\theta \right)\right)\\ =\left[C\left(k_n{p}_{\mathcal{l}-1}^n\left(1\right)-\frac{k_n{p}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q}_{\mathcal{l}-1}^n\left(1\right)\right)+\frac{k_n{q}_{\mathcal{l}-1}^n\left(1\right)-\mathcal{l}{q}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}\right]Y_{\mathcal{l}}^k\left(\theta \right),\mathcal{l}=1,2,\cdots \end{array}$ (10)

withC depending on n and $\mathcal{l}$ .

Remark 4.1. We assume that ${\gamma }_m\ne 0$ to simplify the calculations. If we want to consider this case in the simulations, we approximate it by $\gamma =-0.01$ .

Proof of Theorem 4.1. q is a piecewise constant radial function, $q\left(r\right)=q\left(\left|x\right|\right)$, defined by

$q\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m{\chi }_{\left(r_{m-1},r_m\right)},r=\left|x\right|,$

with $0=r_0<r_1<\cdots <r_{n-1}<r_n=1$, ${\gamma }_m\in ℝ$, and there is no case where ${\gamma }_m={\gamma }_{m+1}$ for all $m\in \left\{\mathrm{1,2,}\cdots \mathrm{,}n-1\right\}$.

We solve the Schrödinger equation with $f=Y_{\mathcal{l}}^k$ for a fixed $\mathcal{l}$. Thus in equation (6) we have $f_{\mathcal{l}k}=1$.

We look for a solution y of (6), of type

$y\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{y}_m\left(r\right),$ (11)

where $y_1$ is the solution of

$\{\begin{array}{l}{r}^2{y}^{″}+2r{y}^{\prime }-\mathcal{l}\left(\mathcal{l}+1\right)y-{\gamma }_1{r}^{2}y=0,r\in \left(0,r_1\right),\\ \underset{r>0,r\to 0}{\lim }y\left(r\right)<\infty ,\end{array}$ (12)

For $m=2,3,\cdot \cdot \cdot ,n-1$, we have a $y_m$ which satisfies

$r^2{y}^{″}+2r{y}^{\prime }-\mathcal{l}\left(\mathcal{l}+1\right)y-{\gamma }_m{r}^{2}y=0,r\in \left(r_{m-1},r_m\right),$ (13)

and $y_n$ in this equation

$\{\begin{array}{l}{r}^2{y}^{″}+2r{y}^{\prime }-\mathcal{l}\left(\mathcal{l}+1\right)y-{\gamma }_n{r}^{2}y=0,r\in \left(r_{n-1},1\right),\\ y\left(1\right)=1,\end{array}$ (14)

and the following compatibility conditions are satisfied

$\{\begin{array}{l}{y}_1\left(r_1\right)=y_2\left(r_1\right)\\ {y^{\prime }}_1\left(r_1\right)={y^{\prime }}_2\left(r_1\right)\\ y_2\left(r_2\right)=y_3\left(r_2\right)\\ {y^{\prime }}_2\left(r_2\right)={y^{\prime }}_3\left(r_2\right)\\ ⋮\\ y_{n-2}\left(r_{n-2}\right)=y_{n-1}\left(r_{n-2}\right)\\ {y^{\prime }}_{n-2}\left(r_{n-2}\right)={y^{\prime }}_{n-1}\left(r_{n-2}\right)\\ y_{n-1}\left(r_{n-1}\right)=y_n\left(r_{n-1}\right)\\ {y^{\prime }}_{n-1}\left(r_{n-1}\right)={y^{\prime }}_n\left(r_{n-1}\right)\end{array}$ (15)

The general solution of the equation

$r^2{y}^{″}+2r{y}^{\prime }-\mathcal{l}\left(\mathcal{l}+1\right)y-{\gamma }_m{r}^{2}y=0,r\in \left(r_{m-1},r_m\right),m=1,2,\cdots ,n,$

is

$y_m\left(r\right)=A_m^{\mathcal{l}}{j}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)+B_m^{\mathcal{l}}{y}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right),\text{if}{\gamma }_m<0,A_m^{\mathcal{l}},B_m^{\mathcal{l}}\in ℝ,$

where $j_{\mathcal{l}}$ and $y_{\mathcal{l}}$ are the Bessel functions of the first and second type, respectively,

$y_m\left(r\right)=A_m^{\mathcal{l}}{r}^{\mathcal{l}}+B_m^{\mathcal{l}}{r}^{-\left(\mathcal{l}+1\right)},\text{if}{\gamma }_m=0,A_m^{\mathcal{l}},B_m^{\mathcal{l}}\in ℝ,$

and

$y_m\left(r\right)=A_m^{\mathcal{l}}{i}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)+B_m^{\mathcal{l}}{\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right),\text{if}{\gamma }_m>0,A_m^{\mathcal{l}},B_m^{\mathcal{l}}\in ℝ,$

where $i_{\mathcal{l}}$ and $k_{\mathcal{l}}$ are the modified Bessel functions of the first and second type, respectively,

For $m=\mathrm{1,2,}\cdot \cdot \cdot \mathrm{,}n$, let us introduce the functions $z_{\mathcal{l}}^m\mathrm{,}{p}_{\mathcal{l}}^m\mathrm{,}{w}_{\mathcal{l}}^m$, and $q_{\mathcal{l}}^m$ such that

● $z_{\mathcal{l}}^m\left(r\right)$ and $p_{\mathcal{l}}^m\left(r\right)$ will be denoted by $j_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)$ or $i_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)$ depending on whether ${\gamma }_m<0$ or ${\gamma }_m>0$,

● $w_{\mathcal{l}}^m\left(r\right)$ and $q_{\mathcal{l}}^m\left(r\right)$ will be denoted by $y_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)$ or ${\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)$ depending on whether ${\gamma }_m<0$ or ${\gamma }_m>0$.

Let pose $k_m=\sqrt{\left|{\gamma }_m\right|},m=1,2,\cdots ,n$.

As the functions $y_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_1\right|}r\right)$ or ${\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_1\right|}r\right)$ go to $-\infty$ when $r\to 0$, we have

$y_1\left(r\right)=A_1^{\mathcal{l}}{z}_{\mathcal{l}}^1\left(r\right)\mathrm{,}\text{or}{A}_1^{\mathcal{l}}{p}_{\mathcal{l}}^1\left(r\right)\mathrm{.}$

For $m=\mathrm{1,2,}\cdots \mathrm{,}n-1$, we have

$y_m\left(r\right)=A_m^{\mathcal{l}}{z}_{\mathcal{l}}^m\left(r\right)+B_m^{\mathcal{l}}{w}_{\mathcal{l}}^m\left(r\right)\left(\text{or}{A}_m^{\mathcal{l}}{p}_{\mathcal{l}}^m\left(r\right)+B_m^{\mathcal{l}}{q}_{\mathcal{l}}^m\left(r\right)\right),$

and

$y_n\left(r\right)=A_n^{\mathcal{l}}{z}_{\mathcal{l}}^n\left(r\right)+B_n^{\mathcal{l}}{w}_{\mathcal{l}}^n\left(r\right)\left(\text{or}{A}_n^{\mathcal{l}}{p}_{\mathcal{l}}^n\left(r\right)+B_n^{\mathcal{l}}{q}_{\mathcal{l}}^n\left(r\right)\right),\text{with}{A}_n^{\mathcal{l}}+B_n^{\mathcal{l}}=1.$

We will need the following derivative formulas.

If $f_{\mathcal{l}}^m$ denotes $j_{\mathcal{l}}^m$, $y_{\mathcal{l}}^m$, $i_{\mathcal{l}}^m$, or ${\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}^m$ with $f_{\mathcal{l}}^m\left(r\right)=f_{\mathcal{l}}\left(k_{m}r\right)$, then ${\left(f_{\mathcal{l}}^m\right)}^{\prime }\left(r\right)=k_m{f^{\prime }}_{\mathcal{l}}\left(k_{m}r\right)$, where ${f^{\prime }}_{\mathcal{l}}$ satisfies

${f^{\prime }}_{\mathcal{l}}\left(z\right)=f_{\mathcal{l}-1}\left(z\right)-\frac{\mathcal{l}+1}{z}{f}_{\mathcal{l}}\left(z\right).$ (16)

From 15 and 16, we have the following system of $\left(2n-2\right)\times \left(2n-2\right)$ equations

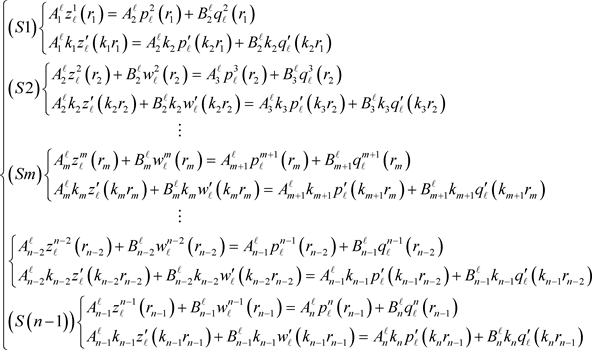(17)

where $A_n^{\mathcal{l}}$ and $B_n^{\mathcal{l}}$ are related by

$A_n^{\mathcal{l}}{p}_{\mathcal{l}}^n\left(1\right)+B_n^{\mathcal{l}}{q}_{\mathcal{l}}^n\left(1\right)=1.$ (18)

We recall (see 8) that our aim is to calculate $y^{\prime }\left(1\right)$ or ${y^{\prime }}_n\left(1\right)$. By condition 18, we are only interesting in finding the unknown $A_n^{\mathcal{l}}$ of the system 17.

Our strategy will be to find the unknowns $A_2^{\mathcal{l}}$ and $B_2^{\mathcal{l}}$ in terms of $A_1^{\mathcal{l}}$ by solving $\left(S1\right)$. And for $m=2,3,\cdots ,n-2$, solve $S\left(m\right)$ to obtain $A_{m+1}^{\mathcal{l}}$ and $B_{m+1}^{\mathcal{l}}$ in terms of $A_1^{\mathcal{l}}$. Then transform the system $S\left(n-1\right)$ into a system of two unknowns $A_1^{\mathcal{l}}$ and $A_n^{\mathcal{l}}$ and two equations. At this point we solve $S\left(n-1\right)$.

For this purpose, we introduce

$F\left(r_m\mathrm{,}{k}_m\mathrm{,}{h}_{\mathcal{l}}^m\mathrm{,}{g}_{\mathcal{l}}^{m+1}\right)=k_{m+1}{h}_{\mathcal{l}}^m\left(r_m\right)g_{\mathcal{l}-1}^{m+1}\left(r_m\right)-k_m{h}_{\mathcal{l}-1}^m\left(r_m\right)g_{\mathcal{l}}^{m+1}\left(r_m\right)\mathrm{.}$ (19)

where $h_{\mathcal{l}}^m$ denotes $z_{\mathcal{l}}^m$ or $w_{\mathcal{l}}^m$, and $g_{\mathcal{l}}^m$ denotes $p_{\mathcal{l}}^m$ or $q_{\mathcal{l}}^m$.

And we will need the following formulas of the Wronskians W, see [17].

$\begin{array}{l}W\left\{j_{\mathcal{l}}\left(z\right)\mathrm{,}{y}_{\mathcal{l}}\left(z\right)\right\}=z^{-2}\mathrm{,}\\ W\left\{i_{\mathcal{l}}\left(z\right)\mathrm{,}{\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}\left(z\right)\right\}=\frac{{\left(-1\right)}^{\mathcal{l}}\pi }{2}{z}^{-2}.\end{array}$ (20)

The problem with including the ${\gamma }_m=0$ case is that the functions $r^{\mathcal{l}}$ and $r^{-\left(\mathcal{l}+1\right)}$ do not satisfy 19. Perhaps a linear combination of different types of functions would make it easy to take into account the case ${\gamma }_m=0$ into the general scheme.

We start by solving (S1) according to $A_1^{\mathcal{l}}$.

$\{\begin{array}{l}{A}_1^{\mathcal{l}}{z}_{\mathcal{l}}^1\left(r_1\right)=A_2^{\mathcal{l}}{p}_{\mathcal{l}}^2\left(r_1\right)+B_2^{\mathcal{l}}{q}_{\mathcal{l}}^2\left(r_1\right)\\ A_1^{\mathcal{l}}{k}_1{z^{\prime }}_{\mathcal{l}}\left(k_1{r}_1\right)=A_2^{\mathcal{l}}{k}_2{p^{\prime }}_{\mathcal{l}}\left(k_2{r}_1\right)+B_2^{\mathcal{l}}{k}_2{q^{\prime }}_{\mathcal{l}}\left(k_2{r}_1\right)\end{array}$ (21)

$A_2^{\mathcal{l}}=\frac{A_1^{\mathcal{l}}}{k_{2}W\left\{p_{\mathcal{l}}^2\left(r_1\right),q_{\mathcal{l}}^2\left(r_1\right)\right\}}\left[k_2{z}_{\mathcal{l}}^1\left(r_1\right){q^{\prime }}_{\mathcal{l}}\left(k_2{r}_1\right)-k_1{q}_{\mathcal{l}}^2\left(r_1\right){z^{\prime }}_{\mathcal{l}}\left(k_1{r}_1\right)\right]$

$A_2^{\mathcal{l}}=\frac{A_1^{\mathcal{l}}}{k_{2}W\left\{p_{\mathcal{l}}^2\left(r_1\right),q_{\mathcal{l}}^2\left(r_1\right)\right\}}\left[k_2{z}_{\mathcal{l}}^1\left(r_1\right)q_{\mathcal{l}-1}^2\left(r_1\right)-k_1{q}_{\mathcal{l}}^2\left(r_1\right)z_{\mathcal{l}-1}^1\left(r_1\right)\right],$

$\boxed{A_2^{\mathcal{l}}=\frac{A_1^{\mathcal{l}}}{k_{2}W\left\{p_{\mathcal{l}}^2\left(r_1\right),q_{\mathcal{l}}^2\left(r_1\right)\right\}}F\left(r_1\mathrm{,}{k}_1\mathrm{,}{z}_{\mathcal{l}}^1\mathrm{,}{q}_{\mathcal{l}}^2\right)}$ (22)

$B_2^{\mathcal{l}}=\frac{A_1^{\mathcal{l}}}{k_{2}W\left\{p_{\mathcal{l}}^2,q_{\mathcal{l}}^2\right\}\left(r_1\right)}\left[k_1{p}_{\mathcal{l}}^2\left(r_1\right){z^{\prime }}_{\mathcal{l}}\left(k_1{r}_1\right)-k_2{z}_{\mathcal{l}}^1\left(r_1\right){p^{\prime }}_{\mathcal{l}}\left(k_2{r}_1\right)\right]$

$B_2^{\mathcal{l}}=\frac{A_1^{\mathcal{l}}}{k_{2}W\left\{p_{\mathcal{l}}^2\left(r_1\right),q_{\mathcal{l}}^2\left(r_1\right)\right\}}\left[k_1{p}_{\mathcal{l}}^2\left(r_1\right)z_{\mathcal{l}-1}^1\left(r_1\right)-k_2{z}_{\mathcal{l}}^1\left(r_1\right)p_{\mathcal{l}-1}^2\left(r_1\right)\right]\mathrm{,}$

$\boxed{B_2^{\mathcal{l}}=-\frac{A_1^{\mathcal{l}}}{k_{2}W\left\{p_{\mathcal{l}}^2\left(r_1\right),q_{\mathcal{l}}^2\left(r_1\right)\right\}}F\left(r_1,k_1,z_{\mathcal{l}}^1,p_{\mathcal{l}}^2\right)}$ (23)

We now solve $\left(Sm\right)$ in terms of $A_m^{\mathcal{l}}$ and $B_m^{\mathcal{l}}$ for $m=2,3,\cdots ,n-2$.

$\{\begin{array}{l}{A}_m^{\mathcal{l}}{z}_{\mathcal{l}}^m\left(r_m\right)+B_m^{\mathcal{l}}{w}_{\mathcal{l}}^m\left(r_m\right)=A_{m+1}^{\mathcal{l}}{p}_{\mathcal{l}}^{m+1}\left(r_m\right)+B_{m+1}^{\mathcal{l}}{q}_{\mathcal{l}}^{m+1}\left(r_m\right)\\ A_m^{\mathcal{l}}{k}_m{z^{\prime }}_{\mathcal{l}}\left(k_m{r}_m\right)+B_m^{\mathcal{l}}{k}_m{w^{\prime }}_{\mathcal{l}}\left(k_m{r}_m\right)=A_{m+1}^{\mathcal{l}}{k}_{m+1}{p^{\prime }}_{\mathcal{l}}\left(k_{m+1}{r}_m\right)+B_{m+1}^{\mathcal{l}}{k}_{m+1}{q^{\prime }}_{\mathcal{l}}\left(k_{m+1}{r}_m\right)\end{array}$ (24)

We call

$F_m^{\mathcal{l}}\left(r_m\right)=A_m^{\mathcal{l}}{z}_{\mathcal{l}}^m\left(r_m\right)+B_m^{\mathcal{l}}{w}_{\mathcal{l}}^m\left(r_m\right)\text{and}{G}_m^{\mathcal{l}}\left(r_m\right)=A_m^{\mathcal{l}}{k}_m{z^{\prime }}_{\mathcal{l}}\left(k_m{r}_m\right)+B_m^{\mathcal{l}}{k}_m{w^{\prime }}_{\mathcal{l}}\left(k_m{r}_m\right).$

$\begin{array}{c}{A}_{m+1}^{\mathcal{l}}=\frac{1}{k_{m+1}W\left(p_{\mathcal{l}}^{m+1}\left(r_m\right),q_{\mathcal{l}}^{m+1}\left(r_m\right)\right)}\left[k_{m+1}{q^{\prime }}_{\mathcal{l}}\left(k_{m+1}{r}_m\right)F_m^{\mathcal{l}}\left(r_m\right)-q_{\mathcal{l}}^{m+1}\left(r_m\right)G_m^{\mathcal{l}}\left(r_m\right)\right]\\ =\frac{1}{k_{m+1}W\left(p_{\mathcal{l}}^{m+1}\left(r_m\right)\mathrm{,}{q}_{\mathcal{l}}^{m+1}\left(r_m\right)\right)}[k_{m+1}{A}_m^{\mathcal{l}}{z}_{\mathcal{l}}^m\left(r_m\right){q^{\prime }}_{\mathcal{l}}\left(k_{m+1}{r}_m\right)+k_{m+1}{B}_m^{\mathcal{l}}{w}_{\mathcal{l}}^m\left(r_m\right){q^{\prime }}_{\mathcal{l}}\left(k_{m+1}{r}_m\right)\\ -k_m{A}_m^{\mathcal{l}}{q}_{\mathcal{l}}^{m+1}\left(r_m\right){z^{\prime }}_{\mathcal{l}}\left(k_m{r}_m\right)-k_m{B}_m^{\mathcal{l}}{q}_{\mathcal{l}}^{m+1}\left(r_m\right){w^{\prime }}_{\mathcal{l}}\left(k_m{r}_m\right)]\mathrm{,}\end{array}$

Using (16), we have

$\begin{array}{c}{A}_{m+1}^{\mathcal{l}}=\frac{1}{k_{m+1}W\left(p_{\mathcal{l}}^{m+1}\left(r_m\right),q_{\mathcal{l}}^{m+1}\left(r_m\right)\right)}[A_m^{\mathcal{l}}\left(k_{m+1}{z}_{\mathcal{l}}^m\left(r_m\right)q_{\mathcal{l}-1}^{m+1}\left(r_m\right)-k_m{q}_{\mathcal{l}}^{m+1}\left(r_m\right)z_{\mathcal{l}-1}^m\left(r_m\right)\right)\\ +B_m^{\mathcal{l}}\left(k_{m+1}{w}_{\mathcal{l}}^m\left(r_m\right)q_{\mathcal{l}-1}^{m+1}\left(r_m\right)-k_m{q}_{\mathcal{l}}^{m+1}\left(r_m\right)w_{\mathcal{l}-1}^m\left(r_m\right)\right)],\end{array}$

$\boxed{A_{m+1}^{\mathcal{l}}=\frac{1}{k_{m+1}W\left(p_{\mathcal{l}}^{m+1}\left(r_m\right),q_{\mathcal{l}}^{m+1}\left(r_m\right)\right)}\left[A_m^{\mathcal{l}}F\left(r_m,k_m,z_{\mathcal{l}}^m,q_{\mathcal{l}}^m\right)+B_m^{\mathcal{l}}F\left(r_m,k_m,w_{\mathcal{l}}^m,q_{\mathcal{l}}^m\right)\right]}$ (25)

$\begin{array}{c}{B}_{m+1}^{\mathcal{l}}=\frac{1}{k_{m+1}W\left(p_{\mathcal{l}}^{m+1}\left(r_m\right),q_{\mathcal{l}}^{m+1}\left(r_m\right)\right)}\left[p_{\mathcal{l}}^{m+1}\left(r_m\right)G_m^{\mathcal{l}}\left(r_m\right)-k_{m+1}{p^{\prime }}_{\mathcal{l}}\left(k_{m+1}{r}_m\right)F_m^{\mathcal{l}}\left(r_m\right)\right]\\ =\frac{1}{k_{m+1}W\left(p_{\mathcal{l}}^{m+1}\left(r_m\right),q_{\mathcal{l}}^{m+1}\left(r_m\right)\right)}[A_m^{\mathcal{l}}{k}_m{p}_{\mathcal{l}}^{m+1}(r_m){z^{\prime }}_{\mathcal{l}}\left(k_m{r}_m\right)+B_m^{\mathcal{l}}{k}_m{p}_{\mathcal{l}}^{m+1}\left(r_m\right){w^{\prime }}_{\mathcal{l}}\left(k_m{r}_m\right)\\ -A_m^{\mathcal{l}}{k}_{m+1}{z}_{\mathcal{l}}^m\left(r_m\right){p^{\prime }}_{\mathcal{l}}\left(k_{m+1}{r}_m\right)-B_m^{\mathcal{l}}{k}_{m+1}{w}_{\mathcal{l}}^m\left(r_m\right){p^{\prime }}_{\mathcal{l}}\left(k_{m+1}{r}_m\right)],\end{array}$

$\begin{array}{c}{B}_{m+1}^{\mathcal{l}}=\frac{1}{k_{m+1}W\left(p_{\mathcal{l}}^{m+1}\left(r_m\right),q_{\mathcal{l}}^{m+1}\left(r_m\right)\right)}[A_m^{\mathcal{l}}\left(k_m{p}_{\mathcal{l}}^{m+1}\left(r_m\right)z_{\mathcal{l}-1}^m\left(r_m\right)-k_{m+1}{z}_{\mathcal{l}}^m\left(r_m\right)p_{\mathcal{l}-1}^{m+1}\left(r_m\right)\right)\\ +B_m^{\mathcal{l}}\left(k_m{p}_{\mathcal{l}}^{m+1}\left(r_m\right)w_{\mathcal{l}-1}^m\left(r_m\right)-k_{m+1}{w}_{\mathcal{l}}^m\left(r_m\right)p_{\mathcal{l}-1}^{m+1}\left(r_m\right)\right)],\end{array}$

$\boxed{B_{m+1}^{\mathcal{l}}=-\frac{1}{k_{m+1}W\left(p_{\mathcal{l}}^{m+1}\left(r_m\right)\mathrm{,}{q}_{\mathcal{l}}^{m+1}\left(r_m\right)\right)}\left[A_m^{\mathcal{l}}F\left(r_m\mathrm{,}{k}_m\mathrm{,}{z}_{\mathcal{l}}^m\mathrm{,}{p}_{\mathcal{l}}^m\right)+B_m^{\mathcal{l}}F\left(r_m\mathrm{,}{k}_m\mathrm{,}{w}_{\mathcal{l}}^m\mathrm{,}{p}_{\mathcal{l}}^m\right)\right]}$ (26)

We define for $m=2,3,\cdots ,n-2$

$I_m\left(\mathcal{l}\right)=\left(\begin{array}{cc}{I}_m^{11}\left(\mathcal{l}\right)& I_m^{12}\left(\mathcal{l}\right)\\ I_m^{21}\left(\mathcal{l}\right)& I_m^{22}\left(\mathcal{l}\right)\end{array}\right)=\left(\begin{array}{cc}F\left(r_m,k_m,z_{\mathcal{l}}^m,p_{\mathcal{l}}^m\right)& F\left(r_m,k_m,z_{\mathcal{l}}^m,q_{\mathcal{l}}^m\right)\\ F\left(r_m,k_m,w_{\mathcal{l}}^m,p_{\mathcal{l}}^m\right)& F\left(r_m,k_m,w_{\mathcal{l}}^m,q_{\mathcal{l}}^m\right)\end{array}\right)$. (27)

$\{\begin{array}{l}{C}_1\left(\mathcal{l}\right)=\frac{1}{k_{2}W\left\{p_{\mathcal{l}}^2\left(r_1\right),q_{\mathcal{l}}^2\left(r_1\right)\right\}}{I}_1^{1,2}\left(\mathcal{l}\right),D_1\left(\mathcal{l}\right)=-\frac{1}{k_{2}W\left\{p_{\mathcal{l}}^2\left(r_1\right),q_{\mathcal{l}}^2\left(r_1\right)\right\}}{I}_1^{1,1}\left(\mathcal{l}\right),\\ C_m\left(\mathcal{l}\right)=\frac{1}{k_{m+1}W\left\{p_{\mathcal{l}}^{m+1}\left(r_m\right),q_{\mathcal{l}}^{m+1}\left(r_m\right)\right\}}\left[C_{m-1}\left(\mathcal{l}\right)I_m^{1,2}\left(\mathcal{l}\right)+D_{m-1}\left(\mathcal{l}\right)I_m^{2,2}\left(\mathcal{l}\right)\right],\\ D_m\left(\mathcal{l}\right)=-\frac{1}{k_{m+1}W\left\{p_{\mathcal{l}}^{m+1}\left(r_m\right),q_{\mathcal{l}}^{m+1}\left(r_m\right)\right\}}\left[C_{m-1}\left(\mathcal{l}\right)I_m^{1,1}\left(\mathcal{l}\right)+D_{m-1}\left(\mathcal{l}\right)I_m^{2,1}\left(\mathcal{l}\right)\right],\end{array}$ (28)

Therefore we have for $m=2,3,\cdots ,n-2$,

$\begin{array}{l}{A}_2^{\mathcal{l}}=C_1\left(\mathcal{l}\right)A_1^{\mathcal{l}},B_2^{\mathcal{l}}=D_1\left(\mathcal{l}\right)A_1^{\mathcal{l}},\\ A_{m+1}^{\mathcal{l}}=C_m\left(\mathcal{l}\right)A_1^{\mathcal{l}},B_{m+1}^{\mathcal{l}}=D_m\left(\mathcal{l}\right)A_1^{\mathcal{l}},\end{array}$ (29)

Then, we have in particular

$A_{n-1}^{\mathcal{l}}=A_1^{\mathcal{l}}{C}_{n-2}\left(\mathcal{l}\right),\text{and}{B}_{n-1}^{\mathcal{l}}=A_1^{\mathcal{l}}{D}_{n-2}\left(\mathcal{l}\right).$

Finally, we solve the (S(n − 1)) system

$\{\begin{array}{l}{A}_{n-1}^{\mathcal{l}}{z}_{\mathcal{l}}^{n-1}\left(r_{n-1}\right)+B_{n-1}^{\mathcal{l}}{w}_{\mathcal{l}}^{n-1}\left(r_{n-1}\right)=A_n^{\mathcal{l}}{p}_{\mathcal{l}}^n\left(r_{n-1}\right)+B_n^{\mathcal{l}}{q}_{\mathcal{l}}^n\left(r_{n-1}\right)\\ A_{n-1}^{\mathcal{l}}{k}_{n-1}{z^{\prime }}_{\mathcal{l}}\left(k_{n-1}{r}_{n-1}\right)+B_{n-1}^{\mathcal{l}}{k}_{n-1}{w^{\prime }}_{\mathcal{l}}\left(k_{n-1}{r}_{n-1}\right)=A_n^{\mathcal{l}}{k}_n{p^{\prime }}_{\mathcal{l}}\left(k_n{r}_{n-1}\right)+B_n^{\mathcal{l}}{k}_n{q^{\prime }}_{\mathcal{l}}\left(k_n{r}_{n-1}\right)\end{array}$

Now we use that

$A_n^{\mathcal{l}}{p}_{\mathcal{l}}^n\left(1\right)+B_n^{\mathcal{l}}{q}_{\mathcal{l}}^n\left(1\right)=1\iff B_n^{\mathcal{l}}=\frac{1}{q_{\mathcal{l}}^n\left(1\right)}-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{A}_n^{\mathcal{l}},$

to obtain

$\{\begin{array}{l}{A}_1^{\mathcal{l}}\left[C_{n-2}\left(\mathcal{l}\right)z_{\mathcal{l}}^{n-1}\left(r_{n-1}\right)+D_{n-2}\left(\mathcal{l}\right)w_{\mathcal{l}}^{n-1}\left(r_{n-1}\right)\right]-A_n^{\mathcal{l}}\left[p_{\mathcal{l}}^n\left(r_{n-1}\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q}_{\mathcal{l}}^n\left(r_{n-1}\right)\right]=\frac{q_{\mathcal{l}}^n\left(r_{n-1}\right)}{q_{\mathcal{l}}^n\left(1\right)}\\ A_1^{\mathcal{l}}\left[C_{n-2}\left(\mathcal{l}\right)k_{n-1}{z^{\prime }}_{\mathcal{l}}\left(k_{n-1}{r}_{n-1}\right)+D_{n-2}\left(\mathcal{l}\right)k_{n-1}{w^{\prime }}_{\mathcal{l}}\left(k_{n-1}{r}_{n-1}\right)\right]-A_n^{\mathcal{l}}\left[k_n{p^{\prime }}_{\mathcal{l}}\left(k_n{r}_{n-1}\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{k}_n{q^{\prime }}_{\mathcal{l}}\left(k_n{r}_{n-1}\right)\right]=\frac{k_n{q^{\prime }}_{\mathcal{l}}\left(k_n{r}_{n-1}\right)}{q_{\mathcal{l}}^n(\; 1\; )}\end{array}$

This system is equivalent to

$\{\begin{array}{l}{M}_{11}{A}_1^{\mathcal{l}}+M_{12}{A}_n^{\mathcal{l}}=\frac{q_{\mathcal{l}}^n\left(r_{n-1}\right)}{q_{\mathcal{l}}^n\left(1\right)}\\ M_{21}{A}_1^{\mathcal{l}}+M_{22}{A}_n^{\mathcal{l}}=\frac{k_n{q^{\prime }}_{\mathcal{l}}\left(k_n{r}_{n-1}\right)}{q_{\mathcal{l}}^n\left(1\right)}\end{array}$ (30)

where

$\{\begin{array}{l}{M}_{11}=C_{n-2}\left(\mathcal{l}\right)z_{\mathcal{l}}^{n-1}\left(r_{n-1}\right)+D_{n-2}\left(\mathcal{l}\right)w_{\mathcal{l}}^{n-1}\left(r_{n-1}\right),\\ M_{12}=-\left(p_{\mathcal{l}}^n\left(r_{n-1}\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q}_{\mathcal{l}}^n\left(r_{n-1}\right)\right),\\ M_{21}=C_{n-2}\left(\mathcal{l}\right)k_{n-1}{z^{\prime }}_{\mathcal{l}}\left(k_{n-1}{r}_{n-1}\right)+D_{n-2}\left(\mathcal{l}\right)k_{n-1}{w^{\prime }}_{\mathcal{l}}\left(k_{n-1}{r}_{n-1}\right),\\ M_{22}=-\left(k_n{p^{\prime }}_{\mathcal{l}}\left(k_n{r}_{n-1}\right)-\frac{p_{\mathcal{l}}^n(1)}{q_{\mathcal{l}}^n(1)}{k}_n{q^{\prime }}_{\mathcal{l}}\left(k_n{r}_{n-1}\right)\right).\end{array}$ (31)

If the solution of this system is $\left(\begin{array}{c}X\left(\mathrm{1,1}\right)\\ X\left(\mathrm{2,1}\right)\end{array}\right)$, the $\mathcal{l}-1$ eigenvalue is

${\lambda }_{\mathcal{l}-1}=X\left(2,1\right)\left(k_n{p^{\prime }}_{\mathcal{l}}\left(k_n\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{k}_n{q^{\prime }}_{\mathcal{l}}\left(k_n\right)\right)+\frac{k_n{q^{\prime }}_{\mathcal{l}}\left(k_n\right)}{q_{\mathcal{l}}^n(1)},\text{with}\mathcal{l}=1,2,\cdots$

Or

${\lambda }_{\mathcal{l}-1}=X\left(2,1\right)\left(k_n{p}_{\mathcal{l}-1}^n\left(1\right)-\frac{k_n{p}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q}_{\mathcal{l}-1}^n\left(1\right)\right)+\frac{k_n{q}_{\mathcal{l}-1}^n\left(1\right)-\mathcal{l}{q}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)},\mathcal{l}=1,2,\cdots$ (32)

where $X\left(2,1\right)$ depends on n and $\mathcal{l}$.

Taking $C=X\left(\mathrm{2,1}\right)$, we have the result. $\square$

Finally, we have obtained an explicit (although rather long and complicated) expression of the Dirichlet-to-Neuman map.

We will illustrate that ${\lambda }_{\mathcal{l}-1}\mathrm{,}\mathcal{l}\ge 1$ in (32) verify the proprieties 1 and 3 in section 2 with various examples. We will do some numerical simulations for this.

4.2. The Case Where the Potential q Is a Continuous Radial Function

In this section, we assume that the potential q is a continuous function with $q\left(r\right)>0$ or $q\left(r\right)<0$ in the interval $\left[\mathrm{0,1}\right]$.

Let introduce the theorems which gives us the expression of the Dirichlet-to-Neuman map when the potential q is a continuous function, based on the results of a piecewise constant radial potential.

For all $\mathcal{l}\in \mathbb{N}$, $p_{\mathcal{l}}^m\left(r\right)$ denotes the Bessel function of the first type $j_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)$ or the Bessel function of the second type $i_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)$, and $q_{\mathcal{l}}^m\left(r\right)$ denotes the modified Bessel function of the first type $y_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)$ or the modified Bessel function of the second type ${\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m\right|}r\right)$.

Theorem 4.2: Let the unit ball B in ${ℝ}^3$ and a continuous radial potential function $q\in {\text{L}}^{\infty }\left(B\right)$ with $q\left(r\right)=q\left(\left|x\right|\right)$ , where $q\left(r\right)>0$ or $q\left(r\right)<0$ , such that the Dirichlet problem for $-\Delta +q$ is well posed.

Let n be a large integer number such that $\left[\mathrm{0,1}\right]={\displaystyle {\cup }_1^n}\left[r_{m-1}\mathrm{,}{r}_m\right]$ with $m=1,\cdots ,n$ and where $r_0=0$ , $r_n=1$ and $r_m-r_{m-1}=\frac{1}{n}$.

Let a denote $k_m=\sqrt{\left|q\left(r_m\right)\right|}$ .

There is,for n enough large integer numbers and $\mathcal{l}=1,2,\cdots$ ,an explicit formula for the Dirichlet-to-Neumann map defined as follows:

$\begin{array}{l}{\Lambda }_q\left(Y_{\mathcal{l}}^k\left(\theta \right)\right)\\ =\left[\tilde{C}\left(\sqrt{\left|q\left(1\right)\right|}{p}_{\mathcal{l}-1}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)-\frac{\sqrt{\left|q\left(1\right)\right|}{p}_{\mathcal{l}}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)}{q_{\mathcal{l}}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)}{q}_{\mathcal{l}-1}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)\right)+\frac{\sqrt{\left|q\left(1\right)\right|}{q}_{\mathcal{l}-1}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)-\mathcal{l}{q}_{\mathcal{l}}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)}{q_{\mathcal{l}}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)}\right]Y_{\mathcal{l}}^k\left(\theta \right).\end{array}$ (33)

with $\tilde{C}$ depending $\mathcal{l}$ , $p_{\mathcal{l}}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)=p_{\mathcal{l}}\left(\sqrt{\left|q\left(1\right)\right|}\right)$ , $p_{\mathcal{l}-1}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)=p_{\mathcal{l}-1}\left(\sqrt{\left|q\left(1\right)\right|}\right)$ , $q_{\mathcal{l}}^{*}\left(1\right)=q_{\mathcal{l}}\left(\sqrt{\left|q\left(1\right)\right|}\right)$ and $q_{\mathcal{l}-1}^{*}\left(1\right)=q_{\mathcal{l}-1}\left(\sqrt{\left|q\left(1\right)\right|}\right)$.

Proof of theorem 4.2. Let introduce $q_i,i=1,2$ be piecewise constant radial functions, $q_i\left(r\right)=q\left(\left|x\right|\right)$, defined by

$q_1\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}q\left(r_{m-1}\right){\chi }_{\left(r_{m-1},r_m\right)},q_2\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}q\left(r_m\right){\chi }_{\left(r_{m-1},r_m\right)},r=\left|x\right|.$

Then from theorem 4.1,

${\Lambda }_{q_1}\left(Y_{\mathcal{l}}^k\left(\theta \right)\right)=\left[C_1\left(k_{n-1}^1{p}_{\mathcal{l}-1}^n\left(1\right)-\frac{k_{n-1}^1{p}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q}_{\mathcal{l}-1}^n\left(1\right)\right)+\frac{k_{n-1}^1{q}_{\mathcal{l}-1}^n\left(1\right)-\mathcal{l}{q}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}\right]Y_{\mathcal{l}}^k\left(\theta \right)\mathrm{,}$

And

${\Lambda }_{q_2}\left(Y_{\mathcal{l}}^k\left(\theta \right)\right)=\left[C_2\left(k_n^2{p}_{\mathcal{l}-1}^n\left(1\right)-\frac{k_n^2{p}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q}_{\mathcal{l}-1}^n\left(1\right)\right)+\frac{k_n^2{q}_{\mathcal{l}-1}^n\left(1\right)-\mathcal{l}{q}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}\right]Y_{\mathcal{l}}^k\left(\theta \right),$

for all $\mathcal{l}=1,2,\cdots$ with $C_1$ and $C_2$ depending on n and $\mathcal{l}$.

If q is increasing, then $q_1\left(r\right)\le q\left(r\right)\le q_2\left(r\right)$ ; if not, $q_1\left(r\right)\le q\left(r\right)\le q_2\left(r\right)$.

We have $\underset{n\to \infty }{\lim }{q}_2\left(r\right)=\underset{n\to \infty }{\lim }{q}_1\left(r\right)=q\left(r\right)$, and then there is $\tilde{C}\left(\mathcal{l}\right)$ such that $\underset{n\to \infty }{\lim }{C}_1\left(n,\mathcal{l}\right)=\underset{n\to \infty }{\lim }{C}_2\left(n,\mathcal{l}\right)=\tilde{C}\left(\mathcal{l}\right)$.

We know that $p_{\mathcal{l}}^n\left(1\right)=p_{\mathcal{l}}\left(k_n\right)$, $p_{\mathcal{l}-1}^n\left(1\right)=p_{\mathcal{l}-1}\left(k_n\right)$, $q_{\mathcal{l}}^n=q_{\mathcal{l}}\left(k_n\right)$, $q_{\mathcal{l}-1}^n=q_{\mathcal{l}-1}\left(k_n\right)$, and $k_n=\sqrt{\left|q\left(1\right)\right|}$, then $p_{\mathcal{l}}^{*}\left(1\right)=p_{\mathcal{l}}\left(\sqrt{\left|q\left(1\right)\right|}\right)$, $p_{\mathcal{l}-1}^{*}\left(1\right)=p_{\mathcal{l}-1}\left(\sqrt{\left|q\left(1\right)\right|}\right)$, $q_{\mathcal{l}}^{*}\left(1\right)=q_{\mathcal{l}}\left(\sqrt{\left|q\left(1\right)\right|}\right)$ and $q_{\mathcal{l}-1}^{*}\left(1\right)=q_{\mathcal{l}-1}\left(\sqrt{\left|q\left(1\right)\right|}\right)$.

Taking n goes to $\infty$ in ${\Lambda }_{q_1}$ and ${\Lambda }_{q_2}$ and using the theorem 4.1, we have the result 33. $\square$

4.3. Numerical Simulations

In this section, we denote $k=\mathcal{l}-1$, and then $k=0,1,2,\cdots$ when $\mathcal{l}=1,2,\cdots$, and then we write ${\lambda }_k$ in the simulations. We will numerically compute the potential q, ${\lambda }_k$, $k-{\lambda }_k$, and $\log \left(\left|k-{\lambda }_k\right|\right)$, $k=0,1,2,\cdots$. We will check numerically if the eigenvalues found in theorems (4.1) and (4.2) verify the properties 1 to 3 introduced in section 2. We will use the Matlab trial version [2021b] for it.

We consider the case where the radial potential is defined by a piecewise constant function

$q\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m{\chi }_{\left(r_{m-1},r_m\right)},r=\left|x\right|,$

where $n\ge 1$, ${\gamma }_m\mathrm{,}{r}_m\in ℝ$, with $m=1,2,\cdots ,n$, $0=r_0<r_1<\cdots <r_{n-1}<r_n=1$,

And the case where the radial potential is defined by a continuous function

$q\left(r\right),r=\left|x\right|,$

with $\left[0,1\right]={\displaystyle {\cup }_1^n}\left[r_{m-1},r_m\right],m=1,\cdots ,n$ where n is a large integer number, $r_0=0$, $r_n=1$ and $r_m-r_{m-1}=\frac{1}{n}$, such that the Dirichlet problem for $-\Delta +q$ is well-posed.

At the first, we consider two examples of piecewise constant radial potential functions where the length of interval $\left[r_{m-1}\mathrm{,}{r}_m\right]$ is arbitrary. We denote Case 1 the case where the potential value at each interval is a random value between −2 and 0, and Case 2 where the potential value at each interval is a random value between −2 and 2.

Secondly, we consider an example of radial continuous potential function in $\left[0,1\right]={\displaystyle {\cup }_1^n}\left[r_{m-1},r_m\right],m=1,\cdots ,n$ where the length of intervals $\left[r_{m-1}\mathrm{,}{r}_m\right]$ is constant and equal to $\frac{1}{n}$.

We denote this example Case 3 taking $q\left(r\right)=0.05+r^2$. We approximate it by two piecewise constant radial potential functions $q_1\left(r\right)$ and $q_2\left(r\right)$ such that $q_1\left(r\right)\le q\left(r\right)\le q_2\left(r\right)$. Using the results of the above section for these cases, we obtain the following results.

4.3.1. Case 1

In this case, in Figure 1 there is an example of the potential q and in Figure 2 we see the corresponding eigenvalues. As excepted, we confirm in Figure 3 and Figure 4. These figures show that the eigenvalues defining the Dirichlet-to-Neuman map in theorem (4.1) verify the 1 to 3 properties considered in Section 2.

Figure 1. Radial potential q(r) in Case 1.

Figure 2. Eigenvalues associated with potential in Case 1.

Figure 3. (Eigenvalues-order)-limit in Case 1.

Figure 4. Confirmation eigenvalues limit in Case 1.

4.3.2. Case 2

In this case, in Figure 5 there is also an example of the potential q and in Figure 6 we see the corresponding eigenvalues. As excepted, we confirm in Figure 7 and Figure 8. These figures show that the eigenvalues defining the Dirichlet-to-Neuman map in the theorem (4.1) verify also the 1 to 3 properties considered in Section 2.

We could do the test for potential positives only and we would have the same results. To do this, we only need to take the absolute values of ${\gamma }_m$ in Case 2. We could also do this test for fixed size intervals; the results will show that the coefficients of the Dirichlet-to-Neuman map in theorem (4.1) are eigenvalues that verify the properties 1 to 3.

4.3.3. Case 3

In this case, in Figure 9 we have the potential curve $q\left(r\right)=0.05+r^2$ in red and this with its approximation by a piecewise constant radial potential in black. In Figure 10 we see the corresponding eigenvalues. As excepted, we confirm in Figure 11 and Figure 12. These figures show that the eigenvalues defining the Dirichlet-to-Neuman map in theorem (4.2) verify the 1 to 3 properties considered in Section 2.

Remark 4.2. Theorems are essential tools to determine the explicit expression of the DN map when f, defined in ${\mathbb{S}}^2$ , is usually written as Fourier series

$f\left(\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{\hat{f}}_{\mathcal{l}k}{Y}_{\mathcal{l}}^k\left(\theta \right)$.

Figure 5. Radial potential q(r) in Case 2.

Figure 6. Eigenvalues associated with potentials in Case 2.

Figure 7. (Eigenvalues-order)-limit in Case 2.

Figure 8. Confirmation eigenvalues limit in Case 2.

Figure 9. Continuous radial potential in Case 3.

Figure 10. Eigenvalues associated with Continuous radial potential in Case 3.

Figure 11. (Eigenvalues-order)-limit in Case 3.

Figure 12. Confirmation eigenvalues limit in Case 3.

These results are very important for studying the inverse problem for our Schrödinger equation. We are interested in the stability of the map that associates a Dirichlet-to-Neumann map to any potential. That is the purpose of the following section.

4.4. Stability

In this section, we are interested in the map

$\begin{array}{l}\Lambda \mathrm{<mo>\; :\; </mo>}{L}^{\infty }\left({\mathbb{S}}^2\right)\to \mathcal{L}\left(H^{1/2}\left({\mathbb{S}}^2\right)\mathrm{,}{H}^{-\mathrm{1\; <mo>\; /\; </mo>2}}\left({\mathbb{S}}^2\right)\right)\\ q\mapsto {\Lambda }_q\mathrm{,}\end{array}$ (34)

where the Dirichlet-to-Neumann map ${\Lambda }_q$ is defined in theorem (4.1). This is an important role in the inverse potential problem, which consists to study its inversion. In the mathematical literature, the Dirichlet to Neumann map is invertible in its range. Taking into account how the measurements for the inverse problem for our Schrödinger equation are made at the ${\mathbb{S}}^2$, we know that there may be some noise in the measured Dirichlet-to-Neumann map and that the noisy version of the real Dirichlet-to-Neumann map may not be a Dirichlet-to-Neumann map corresponding to piecewise constant potentials. Therefore, the stability analysis of $\Lambda$, possibly including a regularization strategy useful for the numerical algorithm, would be interesting.

Let us consider the following map $\Lambda \mathrm{<mo>\; :\; </mo>}q\mapsto {\Lambda }_q$. We are interested in a quantification of the difference of two potentials in the $L^{\infty }$ topology in terms of the distance of their associated Dirichlet-to-Neumann maps. This stability is necessary for all reconstruction algorithms to recover the potential from the Dirichlet-to-Neumann map, see [18] [19]. Then we would like to estimate $q_1-q_2$ in a certain norm defined by

${\Vert {\Lambda }_{q_1}-{\Lambda }_{q_2}\Vert }_{H^{1/2}\to H^{-1/2}}=\underset{f\in H^{1/2}\left({\mathbb{S}}^2\right),f\ne 0}{\sup }\frac{{\Vert \left({\Lambda }_{q_1}-{\Lambda }_{q_2}\right)f\Vert }_{H^{-1/2}\left({\mathbb{S}}^2\right)}}{{\Vert f\Vert }_{H^{1/2}(\; S\; 2\; )}}$

There are stability results when the potential q has some smoothness.

In [20], Joel et al. estimate the difference $q_1-q_2$ in a lower norm in terms of the difference of the Dirichlet-to-Neumann data maps for $\frac{d}{2}<s\in \mathbb{N}$, $d\ge 3$ and ${\Vert q_I\Vert }_{s\mathrm{,}\Omega }\le M$, with d the space dimension.

In [21], for any $d\ge 3$ and $m>0$, Mandache proved that there is $\alpha >0$ such that for every $M>0$ there is $C\left(M\right)>0$, so that ${\Vert q_i\Vert }_{C^m}\le M,i=1,2$ implies

${\Vert q_1-q_2\Vert }_{L^{\infty }\left(\Omega \right)}\le C\left(M\right){\left(\log \left(1+{\Vert {\Lambda }_{q_1}-{\Lambda }_{q_2}\Vert }_{H^{1/2}\to H^{-1/2}}^{-1}\right)\right)}^{-\alpha }\mathrm{,}$ (35)

He shows that (35) is optimal, in the sense that it cannot hold with $\alpha >m\left(2d-1\right)/d$.

According to [21], for arbitrary potentials q, the Lipschitz stability cannot be held.

In [18], M. Salo proved for $q_i\in {\text{L}}^{\infty }\left(\Omega \right)$ that a log-stability estimate holds when $q_1-q_2\in H^{-1}\left(\Omega \right)$, $\Omega \subseteq {ℝ}^n$ is a bounded open set with ${\mathcal{C}}^{\infty }$ boundary, and dimension $d\ge 3$.

We work in the case of piecewise constant arbitrary potentials q. Let us introduce for $n\ge 1$ and finite, $m=1,2,\cdots ,n$ and $0=r_0<r_1<\cdots <r_{n-1}<r_n=1$, the space

$\mathcal{Q}=\left\{q\in {\text{L}}^{\infty }\left(B\right)\mathrm{<mo>\; :\; </mo>}q\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m{\chi }_{\left(r_{m-1}\mathrm{,}{r}_m\right)}\mathrm{,}r=\left|x\right|\mathrm{,}{r}_m\in \left[\mathrm{0,1}\right]\mathrm{,}{\gamma }_m\in ℝ\right\}$

In the case where ${\gamma }_m=0,m=1,2,\cdots ,n$, we approximate it by −0.01.

Here, we establish Lipschitz stability by giving a constant, which depends on n and $\mathcal{l}$ in the dimension n of the potential space.

Our method follows the ideas in [22] [23], where Alessandrini et al. considered special classes of piecewise constant conductivities, and the method of Bereta et al. in [24], for $n\ge 2$.

The Lipschitz stability of an inverse boundary value problem for a Schrödinger type equation is proved by Bereta et al. in [24], for $n\ge 2$.

Here, we study the Lipschitz stability of the map that associates a Dirichlet to Neumann map to any piecewise constant potential q.

Theorem 4.3. Let the unit ball B in ${ℝ}^3$ and the scaled potential $q_i,i=1,2$ verifes

$q_i\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m^i{\chi }_{\left(r_{m-1},r_m\right)},i=1,2,r=\left|x\right|,$

where $n\ge 1$ , ${\gamma }_m^i\mathrm{,}{r}_m\in ℝ$ ,with $m=1,2,\cdots ,n$ and $0=r_0<r_1<\cdots <r_{n-1}<r_n=1$ ,and $k_m^i=\sqrt{\left|{\gamma }_m^i\right|}$ ,such that the Dirichlet problems for $-\Delta +q_i$ is well-posed.Assume that ${\gamma }_n^1\times {\gamma }_n^2>0$ and there is a positive constant M such that

${\Vert q_i\Vert }_{L^{\infty }\left(B\right)}\le M\mathrm{.}$

Then there is a constant $C=C\left(n,M,\mathcal{l}\right)$ ,such that:

$\left|{\gamma }_n^1-{\gamma }_n^2\right|\le C\left({\Vert {\Lambda }_{q_1}-{\Lambda }_{q_2}\Vert }_{H^{1/2}\to H^{-1/2}}\right)\mathrm{.}$ (36)

The result gives us the Lipschitz stability near to the edge ${\mathbb{S}}^2$.

Proof of theorem 4.3. $q_i\in \mathcal{Q}\mathrm{,}i=\mathrm{1,2}$, then we can write

$q_1\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m^1{\chi }_{\left(r_{m-1}^1,r_m^1\right)}$ and $q_2\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m^2{\chi }_{\left(r_{m-1}^2,r_m^2\right)},r=\left|x\right|,$ for $n\ge 1$,

$m=1,2,\cdots ,n$, ${\gamma }_m^1,r_m^1,{\gamma }_m^2,r_m^2\in ℝ$, $0=r_0^1<r_1^1<\cdots <r_{n-1}^1<r_n^1=1$ and $0=r_0^2<r_1^2<\cdots <r_{n-1}^2<r_n^2=1$. We assume that $r_m^1=r_m^2=r_m$ for all $m=0,1,2,\cdots$

We have for all $Y_{\mathcal{l}}^k\in H^{1/2}\left({\mathbb{S}}^2\right)$, $\mathcal{l}\ge 1$,

${\Vert {\Lambda }_{q_1}-{\Lambda }_{q_2}\Vert }_{H^{1/2}\to H^{-1/2}}=\underset{Y_{\mathcal{l}}^k\in H^{1/2}\left({\mathbb{S}}^2\right)\mathrm{,}\mathcal{l}\ge 1}{\sup }{\Vert \left({\Lambda }_{q_1}-{\Lambda }_{q_2}\right)Y_{\mathcal{l}}^k\Vert }_{H^{-1/2}(\; S\; 2\; )}$

From theorem (4.1), we obtain

${\Vert \left({\Lambda }_{q_1}-{\Lambda }_{q_2}\right)Y_{\mathcal{l}}^k\Vert }_{H^{-1/2}\left({\mathbb{S}}^2\right)}^2={\left|\left({\lambda }_{\mathcal{l}-1}^1-{\lambda }_{\mathcal{l}-1}^2\right)\right|}^2{\Vert Y_{\mathcal{l}}^k\Vert }^2\text{for}\text{all}\mathcal{l}\ge 1$

where ${\lambda }_{\mathcal{l}-1}^1\mathrm{,}{\lambda }_{\mathcal{l}-1}^2$ verify the relation (32) for all $n\ge 1$ and finite, $\mathcal{l}\ge 1$. Then

${\Vert {\Lambda }_{q_1}-{\Lambda }_{q_2}\Vert }_{H^{1/2}\to H^{-1/2}}=\underset{\mathcal{l}\ge 1}{\sup }\left|\left({\lambda }_{\mathcal{l}-1}^1-{\lambda }_{\mathcal{l}-1}^2\right)\right|$

Let denote $P_{n\mathrm{,}\mathcal{l}}^1\left[q_1\right]=k_n^1\left(X^1\left(\mathrm{2,1}\right)\left({p^{\prime }}_{\mathcal{l}}\left(k_n^1\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q^{\prime }}_{\mathcal{l}}\left(k_n^1\right)\right)+\frac{{q^{\prime }}_{\mathcal{l}}\left(k_n^1\right)}{q_{\mathcal{l}}^n\left(1\right)}\right)$ where $\left(\begin{array}{c}{X}^1\left(\mathrm{1,1}\right)\\ X^1\left(\mathrm{2,1}\right)\end{array}\right)$ is the solution of 30 associated to $q_1$ and $P_{n\mathrm{,}\mathcal{l}}^1\left[q_1\right]$ the $\mathcal{l}-1$ eingenvalue associated to $q_1$.

And $P_{n\mathrm{,}\mathcal{l}}^2\left[q_2\right]=k_n^2\left(X^2\left(\mathrm{2,1}\right)\left({p^{\prime }}_{\mathcal{l}}\left(k_n^2\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q^{\prime }}_{\mathcal{l}}\left(k_n^2\right)\right)+\frac{{q^{\prime }}_{\mathcal{l}}\left(k_n^2\right)}{q_{\mathcal{l}}^n\left(1\right)}\right)$ where $\left(\begin{array}{c}{X}^2\left(\mathrm{1,1}\right)\\ X^2\left(\mathrm{2,1}\right)\end{array}\right)$ is the solution of 30 associated to $q_2$ and $P_{n\mathrm{,}\mathcal{l}}^2\left[q_2\right]$ the $\mathcal{l}-1$ eigenvalue associated to $q_2$.

We have

${\lambda }_{\mathcal{l}-1}^1-{\lambda }_{\mathcal{l}-1}^2=P_{n,\mathcal{l}}^1\left[q_1\right]-P_{n,\mathcal{l}}^2\left[q_2\right]$

Then

${\Vert {\Lambda }_{q_1}-{\Lambda }_{q_2}\Vert }_{H^{1/2}\to H^{-1/2}}\ge \left|P_{n\mathrm{,}\mathcal{l}}^1\left[q_1\right]-P_{n\mathrm{,}\mathcal{l}}^2\left[q_2\right]\right|$

Let denote $A=X^1\left(2,1\right)\left({p^{\prime }}_{\mathcal{l}}\left(k_n^1\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q^{\prime }}_{\mathcal{l}}\left(k_n^1\right)\right)+\frac{{q^{\prime }}_{\mathcal{l}}\left(k_n^1\right)}{q_{\mathcal{l}}^n\left(1\right)}$, $B=X^2\left(2,1\right)\left({p^{\prime }}_{\mathcal{l}}\left(k_n^2\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q^{\prime }}_{\mathcal{l}}\left(k_n^2\right)\right)+\frac{{q^{\prime }}_{\mathcal{l}}\left(k_n^2\right)}{q_{\mathcal{l}}^n\left(1\right)}$ and $D=\inf \left(A\mathrm{,}B\right)$.

We have $\left|P_{n\mathrm{,}\mathcal{l}}^1\left[q_1\right]-P_{n\mathrm{,}\mathcal{l}}^2\left[q_2\right]\right|\ge \left|k_n^1-k_n^2\right|D\ge \frac{\left|\left|{\gamma }_n^1\right|-\left|{\gamma }_n^2\right|\right|}{2\sqrt{M}}D$ for all $n\ge 1$ finite, $\mathcal{l}\ge 1$ and $M>0$.

We have D is positive real depending on $n\mathrm{,}\mathcal{l}$ and ${\gamma }_n^1\times {\gamma }_n^2>0$. Then for all $M>0$

${\Vert {\Lambda }_{q_1}-{\Lambda }_{q_2}\Vert }_{H^{1/2}\to H^{-1/2}}\ge \frac{D\left(\mathcal{l}\mathrm{,}n\right)}{2\sqrt{M}}\left|{\gamma }_n^1-{\gamma }_n^2\right|\mathrm{.}$

If we take $C\left(\mathcal{l}\mathrm{,}n\mathrm{,}M\right)=\frac{2\sqrt{M}}{D\left(\mathcal{l}\mathrm{,}n\right)}$, then we have the result. $\square$

Remark 4.3. The study of stability for a continuous radial potential function would follow from the study of stability in the case where the potential is a piecewise radial function. It is sufficient to approximate this continuous function by two piecewise radial functions.

5. Conclusion

We can conclude that when we consider that the potential $q\left(r\right)$ is radial function for the Schrödinger equation defined in the unit ball which has no zero on the interval $\left(\mathrm{0,1}\right)$, there exists an explicit formula for the Dirichlet-to-Neumann map given in theorem (4.1) for all piecewise constant radial potential function, and in theorem (4.2) for all continuous radial potential function. We have established a Lipschitz stability result near the edge of the domain with a constant depending on the dimension of the potential space and the order of the eigenvalues. The Lipschitz stability result of the map that associates a Dirichlet to Neumann map to any radial potential q is essential for the study of its inversion. This explicit formula of the Dirichlet-to-Neumann map ${\Lambda }_q\left(f\right)$ in dimension 3 is a first in the literature; it will open the way to the development of important research on inverse problems. In this perspective, we will consider, among other things, the numerical study of the Dirichlet to Neumann map in the unit ball in ${ℝ}^3$, the reconstructing of the potential from the Dirichlet-to-Neumann map both theoretically and numerically, and then the analytical study of the Dirichlet to Neumann map in the case where the potential has one or more zeros on the interval $\left(\mathrm{0,1}\right)$. In addition, Lipschitz type stability in the depth of the domain will be studied by giving an estimation constant.

Data Availability Statement

The data used to support the findings of this study are included in the article.

Acknowledgements

The author is supported by “Mujeres for África” foundation in its 6^th Edition of “Science by Women” program from SPAIN, to stay in ICMAT and do research.

She thanks J. A. Barceló in Universidad Politécnica de Madrid, D. Faraco in ICMAT-Universidad Autónoma de Madrid and C. Castro in Universidad Politécnica de Madrid, for their contribution to this research.

Appendix

We consider the spherical Bessel functions

$j_{\mathcal{l}}\left(r\right)=\sqrt{\frac{\pi }{2r}}{J}_{\mathcal{l}+\frac{1}{2}}\left(r\right),y_{\mathcal{l}}\left(r\right)=\sqrt{\frac{\pi }{2r}}{Y}_{\mathcal{l}+\frac{1}{2}}\left(r\right),$ (37)

that satisfies the equation

$r^2{y}^{″}+2r{y}^{\prime }+\left(r^2-\mathcal{l}\left(\mathcal{l}+1\right)\right)y=0.$

The modified spherical Bessel functions

$i_{\mathcal{l}}\left(r\right)=\sqrt{\frac{\pi }{2r}}{I}_{\mathcal{l}+\frac{1}{2}}\left(r\right),k_{\mathcal{l}}\left(r\right)=\sqrt{\frac{\pi }{2r}}{K}_{\mathcal{l}+\frac{1}{2}}\left(r\right),$ (38)

that satisfies the equation.

If $f_{\mathcal{l}}=j_{\mathcal{l}},y_{\mathcal{l}},i_{\mathcal{l}},{\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}$ then

${f^{\prime }}_{\mathcal{l}}\left(r\right)=f_{\mathcal{l}-1}-\frac{\mathcal{l}+1}{r}{f}_{\mathcal{l}}\left(r\right).$ (39)

Conflicts of Interest

The author declares that there is no conflict of interest.

References

[1]	Calderón, A.P. (1980) On an Inverse Boundary Value Problem. Seminar on Numerical Analysis and Its Applications to Continuum Physics, Soc Brasil Mat, Ro de Janeiro, 65-73.
[2]	Calderón, A.P. (1963) Boundary Value Problems for Elliptic Equations. Outlines of the Joint Soviet-American Symposium on Partial Differential Equations, Novisibirsk, August 1963, 303-304.
[3]	Gunther, U. (2009) Electrical Impedance Tomography and Calderón’s Problem. Inverse Problems, 25, Article No. 123011.
[4]	Girouard, A. and Polterovich, I. (2014) Spectral Geometry of the Steklov Problem.
[5]	Rüland, A. (2014) On some Quantitative Unique Continuation Properties of Fractional Schrödinger Equations: Doubling, Vanishing Order and Nodal Domain Estimates.
[6]	Bellova, K. and Lin, F. (2014) Nodal Sets of Steklov Eigenfunctions. Preprint: arXiv: 1402-4323.
[7]	Zelditch, S. (2014) Measure of Nodal Sets of Analytic Steklov Eigenfunctions
[8]	Zhu, J. (2014) Doubling Property and Vanishing Order of Steklov Eigenfunctions.
[9]	Akhmetgaliyev, E., Kao, C.Y. and Osting, B. (2017) Computational Methods for Extremal Steklov Problems. SIAM Journal on Control and Optimization, 55, 1226-1240. https://doi.org/10.1137/16M1067263
[10]	Dhahbi, A., Chargui, Y. and Trablesi, A. (2019) A New Class of Exactly Solvable Models within the Schrödinger Equation with Position Dependent Mass. Journal of Applied Mathematics and Physics, 7, 1013-1026. https://doi.org/10.4236/jamp.2019.75068
[11]	Chen, J., Lu, W.J., Xiao, H.Y., Wang, Y.N. and Tan, X. (2019) Entropy Number of Diagonal Operator. Journal of Applied Mathematics and Physics, 7, 738-745. https://doi.org/10.4236/jamp.2019.73051
[12]	Greenleaf, A. and Uhlmann, G. (2000) Local Uniqueness for the Dirichlet-to-Neuman Map via the Two-Plane Transform.
[13]	Imanuvilov, O.Y., Uhlmann, G. and Yamatoko, M. (2015) The Dirichlet-to-Neumann Map in Two Dimensions. Advances in Mathematics, 281, 578-593. https://doi.org/10.1016/j.aim.2015.03.026
[14]	Sagrario, L. and Susana, M. (2021) The Dirichlet-to-Neumann Map in a Disk with a One-Step Radial Potential: An Analytical and Numerical Study. Mathematics, 9, Article No. 794. https://doi.org/10.3390/math9080794
[15]	Mueller, J. and Siltanen, S. (2012) Linear and Nonlinear Inverse Problems with Practical Applications. Society for Industrial and Applied Mathematics, Philadelphia. https://doi.org/10.1137/1.9781611972344
[16]	Faddeev, L.D. (1966) Increasing Solutions of the Schrödinger Equation. Soviet Physics Doklady, 10, 1033-1035.
[17]	Abramowitz, M. and Stregun, I.A. (1954) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. National Science Foundation and the Massachusetts Institute of Technology, Cambridge, 15-16.
[18]	Mikko, S. (2008) The Calderón’s Problem-Lecture Notes. Spring, Departement of Mathematics, University of Helsinki, Helsinki.
[19]	Choudhury, A.P. and Heck H. (2017) Increasing Stability for the Inverse Problem for the Schrödinger Equation, Mathematics. Mathematical Methods in the Applied Sciences, 41, 606-614. https://doi.org/10.1002/mma.4632
[20]	Joel, F., Mikko, S. and Gunther, U. (2001) The Calderón Problem—An Introduction to Inverse Problems. Measurement Science and Technology, 12, 1061-1068. https://doi.org/10.1088/0957-0233/12/8/311
[21]	Mandache, N. (2001) Exponential Instability in an Inverse Problem for Schrödinger Equation. Inverse Problems, 17, 1435-1444. https://doi.org/10.1088/0266-5611/17/5/313
[22]	Alessandrini, G. and Vessella, S. (2005) Lipschitz Stability for the Inverse Conductivity Problem. Advances in Applied Mathematics, 35, 207-241. https://doi.org/10.1016/j.aam.2004.12.002
[23]	Alessandrini, G., De Hoop, M.V., Graburro, R. and Sincich, E. (2017) Lipschitz Stability for the Electrostatic Inverse Boundary Value Problem with Piecewise Linear Conductivities. Journal de Mathématiques Pures et Appliquées, 107, 638-664. https://doi.org/10.1016/j.matpur.2016.10.001
[24]	Beretta, E. and Francini, E. (2011) Lipschitz Stability for the Electrical Impedance Tomography Problem: The Complex Case. Communications in Partial Differential Equations, 36, 1723-1749. https://doi.org/10.1080/03605302.2011.552930