Comparative Semantics of Fuzzy Argumentation under the Łukasiewicz t-Norm

Shuangyan Zhao

School of Mathematics and Statistics, Shandong Normal University, Jinan, China.

DOI: 10.4236/eng.2022.141004                

Abstract

Dung’s theory of argumentation frameworks (AF) has been applied in many fields of artificial intelligence. The arguments and attack relation are generally partly believed due to the uncertainty in the process of mining them. Fuzzy AFs catch uncertainty in AFs by associating fuzzy degrees with the arguments or the attacks. Among the various semantics of fuzzy AFs, the comparative semantics develops and defines Dung’s extensions in the form of fuzzy sets. However, the comparative semantic system only puts forward some basic concepts, and has not been deeply studied in terms of algorithms and properties. This paper studies the comparative semantics of fuzzy AFs based on the Łukasiewicz t-norm in a more in-depth and comprehensive manner. This work is not only a supplement and improvement to comparative semantic in theory, but also beneficial to the calculation and fast identification of its various extensions (based on the Łukasiewicz t-norm).

Keywords

Argumentation, Fuzzy Set, Fuzzy Argumentation Framework, Łukasiewicz t-Norm, Comparative Semantics

1. Introduction

Argumentation has become more and more important as a hot topic in the field of artificial intelligence. A Dung’s AF [1] consists of a set of arguments and an attack relation between them. Given such a graph, its main task is to select arguments that can be accepted by rational agents, more precisely, those that can be accepted together. Such sets are called “extensions”. After more than twenty years, Dung’s AF theory has been applied in many fields, such as the law [2], decision making [3], nonmonotonic reasoning [4].

In order to meet the actual needs, various extensions have been proposed. For example, the support relation [5], joint attack [6] and recursive attack [7] are considered in Dung’s AFs. The arguments and attacks between them are generally partly believed due to the uncertainty in the process of mining them. It may be useful to quantify the uncertainty associated with each argument. In order to capture the uncertainty in AFs, fuzzy AFs came into being, such as [8] [9] [10] [11], in which arguments and attacks are associated with fuzzy degrees or trust degrees to indicate the trust degrees. Fuzzy argumentation system involves the theories of fuzzy sets [12], fuzzy logic [13], control and decision-making [14], etc.

The semantics of fuzzy AFs has been proposed in many works, such as [9] [10] [11]. In the semantic research of fuzzy AFs, the object of screening is usually not the set of arguments, but the fuzzy degree of each argument. Similar to Dung’s theory, in the process of building the semantics of fuzzy AFs, acceptability is the basis for constructing extension-based semantics. [9] introduced x-conflict-free sets, y-admissible sets, y-preferred extensions, and z-stable extensions. [10] proposed the concepts of sufficient attacks and weakening defense based on the Gödel t-norm, and established Gödel semantic system in the form of fuzzy argument sets on this basis. Among the many defense methods, comparative defense [11] is a novel and natural defense method. However, there are relatively few semantic studies based on this defensive style. This paper is an exploration of the semantics of this type. The basis of comparative defense is the strength of the attack (str) from a fuzzy argument to another fuzzy argument. For comparative semantics, conflict-freeness in the semantics requires the str to be 0. If the str of a weak attack is 0, then a nilpotent t-norm is needed to calculate the str. In this paper, we choose the most common nilpotent t-norm—the Łukasiewicz t-norm—to calculate the str, thereby obtaining a special kind of comparative semantics.

In this paper, we conduct an in-depth study on the comparative semantics under the Łukasiewicz t-norm, and discuss some numerical properties of the conflict-free sets, the admissible extensions, the complete extensions, and the stable extensions of the semantics in turn. This paper has two contributions: On the one hand, this work enriches the theory of comparative semantics of fuzzy AFs. On the other hand, this work makes the application of comparative semantics more convenient. For example, in applications, these numerical properties of this semantics can effectively promote the calculation and identification of the extensions, especially the identification of complete extensions in fuzzy AFs without cycles.

The contents will be arranged as follows. Section 2 recalls some necessary basic knowledge: the fuzzy set theory and the fuzzy AFs with comparing acceptability (FAFCA) theory. Section 3 introduces a system of extension-based comparative semantics under the Łukasiewicz t-norm. Section 4 compares our semantics with other semantics. Section 5 summarizes and remarks about the future work.

2. Basic Knowledge

This work characterizes the fuzzy AFs by fuzzy set theory. Hence, let’s recall some useful notions in fuzzy sets [12] and FAFCA theory [11].

2.1. Fuzzy Set Theory

In this paper, the truth values of arguments and attacks are drawn from the unit interval $\left[\text{0,1}\right]$, with the natural order $\le$.

Let U be a universe set. For any $S\subseteq U$, its characteristic function ${\chi }_S$ is a mapping from U to $\left\{0,1\right\}$, where $\forall x\in U$,

${\chi }_S\left(x\right)=\{\begin{array}{ll}1,\hfill & \text{if}x\in S,\hfill \\ 0,\hfill & \text{if}x\in S\setminus U.\hfill \end{array}$

Given a universe set U, a fuzzy set is a pair $\left(U,S\right)$, where S is a function $\mathcal{S}:U\to \left[0,1\right]$. In general, $\left(U,S\right)$ is short for S.

If the universe of a fuzzy set S is finite, S is commonly represented in the form $\left\{\left(x,\mathcal{S}\left(x\right)\right):x\in U\text{and}\mathcal{S}\left(x\right)\ne 0\right\}$.

For any set $S\subseteq U$, we call S a crisp set. ${\chi }_S$ is the fuzzy form of the set S.

A fuzzy set ${\mathcal{S}}_1$ is included in another fuzzy set ${\mathcal{S}}_2$, denoted by $S_1\subseteq S_2$, if $\forall x\in U$, ${\mathcal{S}}_1\left(x\right)\le {\mathcal{S}}_2\left(x\right)$.

A fuzzy set S, whose support is a single element $x\in U$, is called a fuzzy point and denoted by $\left(x,\mathcal{S}\left(x\right)\right)$.

In fuzzy AFs, an argument together with its fuzzy degree is a pair $\left(A,a\right)$. For convenience, we call the pair $\left(A,a\right)$ a fuzzy argument.

Additionally, if $Args$ is the set of all the arguments, a function $\mathcal{S}:Args\to \left[0,1\right]$, assigning each argument a fuzzy degree, is called a fuzzy set of arguments.

The next two t-norms will be used in this paper.

• The Gödel t-norm: $x\wedge y=\min \left\{x,y\right\}$, $\forall x,y\in \left[0,1\right]$.

• The Łukasiewicz t-norm: $x\wedge y=\max \left\{0,x+y-1\right\}$, $\forall x,y\in \left[0,1\right]$.

2.2. FAFCA Theory

This subsection briefly reviews the FAFCA theory [11]. Give a finite argument set $Args$, and the form of the fuzzy AF based on this set is defined as follows:

Definition 1 Given a set of arguments $Args$, a fuzzy AF is a tuple $\left(\mathcal{A},\rho \right)$, where $\mathcal{A}:Args\to \left[0,1\right]$ assigns each argument in $Args$ a fuzzy degree, and $\rho :Args\times Args\to \left[0,1\right]$ assigns a fuzzy degree to each attack over $Args$.

$\rho \left(\left(A,B\right)\right)$ represents the fuzzy degree of the attack between arguments A and B. It is written as $\rho \left(A\to B\right)$ or ${\rho }_{AB}$ for convenience below.

Definition 2 In a fuzzy AF $\left(\mathcal{A},\rho \right)$, for fuzzy arguments $\left(A,a\right)$ and $\left(B,b\right)$, the value $a\wedge b\wedge \rho \left(A\to B\right)$ is called the strength of the attack from $\left(A,a\right)$ to $\left(B,b\right)$, denoted by $str\left(\left(A,a\right),\left(B,b\right)\right)$.

Definition 3 In a fuzzy AF $\left(\mathcal{A},\rho \right)$, given two fuzzy arguments $\left(A,a\right)$ and $\left(B,b\right)$, if $str\left(\left(A,a\right),\left(B,b\right)\right)=0$, then we say $\left(A,a\right)$ tolerably attacks $\left(B,b\right)$ ; otherwise, we say $\left(A,a\right)$ sufficiently attacks $\left(B,b\right)$.

Definition 4 Conflict-freeness: Let $\left(\mathcal{A},\rho \right)$ be a fuzzy AF. A fuzzy set $\mathcal{E}\subseteq \mathcal{A}$ is conflict-free if there are no sufficient attacks between the fuzzy arguments in $\mathcal{E}$.

Acceptability: Let $\mathcal{E}\subseteq \mathcal{A}$ be a fuzzy set of arguments and $\left(A,a\right)\in \mathcal{A}$ be a fuzzy argument. A is acceptable w.r.t. (or defended by) $\mathcal{A}$, if $\forall \left(B,b\right)\in \mathcal{A}$, $\exists \left(C,c\right)\in \mathcal{E}$, s.t. $Astr\left(\left(C,c\right),\left(B,b\right)\right)\ge str\left(\left(B,b\right),\left(A,a\right)\right)$.

Admissibility: A conflict-free set $\mathcal{E}\subseteq \mathcal{A}$ is admissible if it defends every fuzzy element in it.

Complete extension: An admissible extension $\mathcal{E}\subseteq \mathcal{A}$ is a complete extension, if every fuzzy element it defends is in $\mathcal{E}$.

Preferred extension: A preferred extension is a maximal (w.r.t. set inclusion) admissible set.

Grounded extension: The grounded extension is the least complete extension.

Stable extension: A stable extension $\mathcal{E}\subseteq \mathcal{A}$ is a conflict-free extension, which sufficiently attacks every fuzzy arguments in $\mathcal{A}\setminus E$, i.e., $\forall \left(B,b\right)\notin \mathcal{A}$, $\mathcal{E}$ sufficiently attacks $\left(A,a\right)$.

3. Comparative Semantics of Fuzzy Argumentation under the Łukasiewicz t-Norm

In this section, we introduce comparative semantics of fuzzy argumentation under the Łukasiewicz t-norm. We use the Łukasiewicz t-norm to ignore some weak attacks between the fuzzy arguments. Use the Łukasiewicz t-norm to calculate the str, the calculation formula can be simplified. The reason for choosing the Łukasiewicz t-norm is that the conflict-freeness in comparative semantics requires that the str between fuzzy arguments is 0. Hence, if a rational agent wants to ignore some weak attacks in applications, a nilpotent t-norm can be selected such as the Łukasiewicz t-norm. Otherwise, if any minor attacks should not be ignored, a rational agent can choose other t-norms, such as a Gödel t-norm, a product t-norm, etc. Also, as the most famous nilpotent t-norm, the Łukasiewicz case of fuzzy AF has some special properties. And they will be discussed in this section. First, we redefine the str using the Łukasiewicz t-norm.

Definition 5 Given a fuzzy AF $\left(\mathcal{A},\rho \right)$.

$str\left(\left(A,a\right),\left(B,b\right)\right)=\max \left\{0,a+\max \left\{0,\rho \left(A\to B\right)+b-1\right\}-1\right\}.$

is the attack strength (str) from $\left(A,a\right)$ to $\left(B,b\right)$.

Particularly, we denote the str from a fuzzy set $\mathcal{E}$ to a fuzzy argument $\left(A,a\right)$ as

$str\left(\mathcal{E},\left(A,a\right)\right)=\underset{C\in Args}{\max }str\left(\left(C,\mathcal{E}\left(C\right)\right),\left(A,a\right)\right).$

3.1. Conflict-Freeness

Theorem 1 $\mathcal{E}\subseteq \mathcal{A}$ is conflict-free, if $\forall A,B\in Args$,

$\mathcal{E}\left(A\right)+\rho \left(A\to B\right)+\mathcal{E}\left(B\right)\le 2$.

Proof. $\mathcal{E}\subseteq \mathcal{A}$ is conflict-free, if $\forall A,B\in Args$,

$\max \left\{0,\mathcal{E}\left(A\right)+\max \left\{0,\mathcal{E}\left(B\right)+\rho \left(A\to B\right)-1\right\}-1\right\}=0$,

which is equivalent to

$\mathcal{E}\left(A\right)+\rho \left(A\to B\right)+\mathcal{E}\left(B\right)\le 2$.

Corollary 1 In a fuzzy AF $\left(\mathcal{A},\rho \right)$, suppose all the attacks are crisp, i.e. their values are either 0 or 1.

$\mathcal{E}\subseteq \mathcal{A}$ is conflict-free, if $\forall A,B\in Args$, $\mathcal{E}\left(A\right)+\mathcal{E}\left(B\right)\le 1$.

3.2. Acceptability

Theorem 2 $\mathcal{E}\subseteq \mathcal{A}$ defends $\left(A,a\right)$, if $\forall \left(B,b\right)\in \mathcal{A}$, which sufficiently attacks $\left(A,a\right)$, $\exists C\in Args$, s.t. $\mathcal{E}\left(C\right)+\rho \left(C\to B\right)\ge a+\rho \left(B\to A\right)$

Proof. Since $\mathcal{E}\subseteq \mathcal{A}$ defends $\left(A,a\right)$, we have $\forall \left(B,b\right)\in \mathcal{A}$, $\exists C\in Args$, s.t.

$str\left(\left(C,\mathcal{E}\left(C\right)\right),\left(B,b\right)\right)\ge str\left(\left(B,b\right),\left(A,a\right)\right)$,

i.e.

$\max \left\{0,\max \left\{0,\mathcal{E}\left(C\right)-1+{\rho }_{CB}\right\}+b-1\right\}\ge \max \left\{0,\max \left\{0,a+{\rho }_{BA}-1\right\}+b-1\right\}.$

If $\left(B,b\right)$ sufficiently attacks $\left(A,a\right)$, i.e. $str\left(\left(B,b\right),\left(A,a\right)\right)>0$, then we have

$\max \left\{0,\max \left\{0,\mathcal{E}\left(C\right)-1+{\rho }_{CB}\right\}+b-1\right\}\ge \max \left\{0,\max \left\{0,a+{\rho }_{BA}-1\right\}+b-1\right\}>0.$

Hence,

$\mathcal{E}\left(C\right)-1+{\rho }_{CB}+b-1\ge a+{\rho }_{BA}-1+b-1>0,$

i.e.

$\mathcal{E}\left(C\right)+\rho \left(C\to B\right)\ge a+\rho \left(B\to A\right).$

3.3. Admissibility

Theorem 3 In a fuzzy AF $\left(\mathcal{A},\rho \right)$, a conflict-free set $\mathcal{E}\subseteq \mathcal{A}$ is admissible, if $\forall A,B\in Args$, $\exists C\in Args$, s.t.

$\max \left\{0,\max \left\{0,\mathcal{E}\left(C\right)-1+{\rho }_{CB}\right\}+b-1\right\}\ge \max \left\{0,\max \left\{0,a+{\rho }_{BA}-1\right\}+b-1\right\}>0.$

Proof. ( $\Rightarrow$ ) Since $\mathcal{E}\subseteq \mathcal{A}$ is conflict-free,

$\mathcal{E}\left(C\right)+\rho \left(C\to B\right)+\mathcal{E}\left(B\right)\le 2,$ $\mathcal{E}\left(B\right)+\rho \left(B\to A\right)+\mathcal{E}\left(A\right)\le 2,$

$\mathcal{E}\subseteq \mathcal{A}$ is admissible. Suppose $\forall A,B\in Args$, B attacks A, then $\exists C\in Args$,

$str\left(\left(C,\mathcal{E}\left(C\right)\right),\left(B,\mathcal{E}\left(B\right)\right)\right)\ge str\left(\left(B,\mathcal{E}\left(B\right)\right),\left(A,\mathcal{E}\left(A\right)\right)\right).$

Hence,

$\max \left\{\mathcal{E}\left(C\right)+\rho \left(C\to B\right),2-\mathcal{E}\left(B\right)\right\}\ge \max \left\{\mathcal{E}\left(A\right)+\rho \left(B\to A\right),2-\mathcal{E}\left(B\right)\right\}.$

( $\Leftarrow$ ) Obvious!

Corollary 2 Given a fuzzy set $\mathcal{E}\subseteq \mathcal{A}$ in a fuzzy AF $\left(\mathcal{A},\rho \right)$, where $\rho$ is crisp. Then $\mathcal{E}$ is admissible, if $\forall A,B\in Args$, $\exists C\in Args$, s.t.

$\max \left\{\mathcal{E}\left(C\right),1-\mathcal{E}\left(B\right)\right\}\ge \max \left\{\mathcal{E}\left(A\right),1-\mathcal{E}\left(B\right)\right\}.$

3.4. Complete Extension

In a fuzzy AF $\left(\mathcal{A},\rho \right)$, for any $A\in Args$, $Att\left(A\right)$ is defined as:

$Att\left(A\right)=\left\{B:str\left(\left(B,\mathcal{A}\left(B\right)\right),\left(A,\mathcal{A}\left(A\right)\right)\right)>0\right\}.$

The following lemma is obvious.

Lemma 1 In a fuzzy AF $\left(\mathcal{A},\rho \right)$, $\mathcal{E}\subseteq \mathcal{A}$ is a complete extension, $\forall A\in Args$, if $Att\left(A\right)=\varnothing$, then $\mathcal{E}\left(A\right)=\mathcal{A}\left(A\right)$.

As shown in the following figure, argument $\left(A,\mathcal{A}\left(A\right)\right)$ is sufficiently attacked, and there is no argument to defend it, obviously $\mathcal{E}\left(A\right)<\mathcal{A}\left(A\right)$.

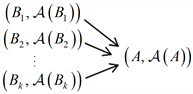
Lemma 2 In a fuzzy AF $\left(\mathcal{A},\rho \right)$, $\mathcal{E}\subseteq \mathcal{A}$ is a complete extension. $\forall A\in Args$, $Att\left(A\right)\ne \varnothing$, if $\forall B\in Att\left(A\right)$, $Att\left(B\right)=\varnothing$, then

$\mathcal{E}\left(A\right)=\min \left\{2-\mathcal{A}\left(B\right)-\rho \left(B\to A\right):B\in Att\left(A\right)\right\}.$

Proof. Obviously, $\left(A,\mathcal{E}\left(A\right)\right)$ is not sufficiently attacked by any fuzzy arguments. It is only necessary to show $\left(A,a\right)$ ( $\forall a>\mathcal{E}\left(A\right)$ ) is sufficiently attacked by some fuzzy argument $\left(B,\mathcal{E}\left(B\right)\right)$.

Suppose $a>\mathcal{E}\left(A\right)$,

i.e. $a>\min \left\{2-\mathcal{A}\left(B\right)-\rho \left(B\to A\right):B\in Att\left(A\right)\right\}$, which equals

$a>\min \left\{1-\max \left\{0,\mathcal{A}\left(B\right)+\rho \left(B\to A\right)-1\right\}:B\in Att\left(A\right)\right\}$.

Then $\exists B\in Att\left(A\right)$, s.t.

$a+\max \left\{0,\mathcal{A}\left(B\right)+\rho \left(B\to A\right)-1\right\}-1>0$,

i.e. $str\left(\left(B,\mathcal{E}\left(B\right)\right),\left(A,a\right)\right)>0$, then $\left(A,a\right)$ is sufficiently attacked by $\left(B,\mathcal{E}\left(B\right)\right)$.

Lemma 3 Given a complete extension $\mathcal{E}\subseteq \mathcal{A}$, $\forall A\in Args$, $Att\left(A\right)\ne \varnothing$, $\forall B\in Att\left(A\right)$, and $Att\left(B\right)=\varnothing$, then

$\mathcal{E}\left(A\right)=\min \left\{\underset{B\in Att\left(A\right)}{\min }\underset{C\in Att\left(B\right)}{\max }\left\{\mathcal{E}\left(C\right)+\rho \left(C\to B\right)-\rho \left(B\to A\right)\right\},\mathcal{A}\left(A\right)\right\}$.

Proof. Let’s calculate the value $\mathcal{E}\left(A\right)$ from the values of $\mathcal{E}\left(C\right)$ and $\mathcal{E}\left(B\right)$.

From the definition of defense (or acceptability), we know the fuzzy set $\mathcal{E}$ can defend $\left(A,a\right)$, if and only if for $\left(B,b\right)$ sufficiently attacks $\left(A,a\right)$, $\exists C\in Att\left(B\right)$, s.t.

$str\left(\left(C,\mathcal{E}\left(C\right)\right),\left(B,b\right)\right)\ge str\left(\left(B,b\right),\left(A,a\right)\right)>0.$

Thus,

$\max \left\{0,\mathcal{E}\left(C\right)+{\rho }_{CB}-1\right\}+b-1\ge \max \left\{0,a+{\rho }_{BA}-1\right\}+b-1>0.$

For $b-1\le 0$, we have $\max \left\{0,a+\rho \left(B\to A\right)-1\right\}>0$. Therefore, we get

$\mathcal{E}\left(C\right)+\rho \left(C\to B\right)\ge a+\rho \left(B\to A\right),$

i.e. $\mathcal{E}\left(C\right)+\rho \left(C\to B\right)-\rho \left(B\to A\right)\ge a$.

As a result, we have

$\begin{array}{c}\mathcal{E}\left(A\right)=\underset{B\in Att\left(A\right)}{\min }\left\{\underset{C\in Att\left(B\right)}{\max }\left\{\max \left\{a:a\le \mathcal{E}\left(C\right)+\rho \left(C\to B\right)-\rho \left(B\to A\right)\right\}\right\}\right\}\\ =\underset{B\in Att\left(A\right)}{\min }\left\{\underset{C\in Att\left(B\right)}{\max }\left\{\mathcal{E}\left(C\right)+\rho \left(C\to B\right)-\rho \left(B\to A\right)\right\}\right\}.\end{array}$

Together with $a\le \mathcal{A}\left(A\right)$, we have

$\mathcal{E}\left(A\right)=\min \left\{\underset{B\in Att\left(A\right)}{\min }\underset{C\in Att\left(B\right)}{\max }\left\{\mathcal{E}\left(C\right)+\rho \left(C\to B\right)-\rho \left(B\to A\right)\right\},\mathcal{A}\left(A\right)\right\}.$

Combining the above three lemmas together, we have the following proposition.

Theorem 4 Given a complete extension $\mathcal{E}\subseteq \mathcal{A}$, for every $A\in Args$, the value $\mathcal{E}\left(A\right)$ is the minimum of the values calculated by Lemmas 1, 2 and 3.

This Theorem 4 can be applied to check whether a fuzzy set is complete. It also can be applied to calculate the complete extensions in fuzzy AFs without sufficient attack cycles.

3.5. Stable Extension

Theorem 5. In a fuzzy AF $\left(\mathcal{A},\rho \right)$, $\mathcal{E}\subseteq \mathcal{A}$ is a stable extension, if $\forall A,B\in Args$, $\mathcal{E}\left(A\right)+\rho \left(A\to B\right)+\mathcal{E}\left(B\right)\le 2$, and either $\mathcal{E}\left(A\right)=\mathcal{A}\left(A\right)$, or $\exists C\in Args$, s.t.

$\mathcal{E}\left(A\right)+\mathcal{E}\left(C\right)+\rho \left(C\to A\right)=2.$

Proof. ( $\Rightarrow$ ) Suppose $\mathcal{E}\subseteq \mathcal{A}$ is a stable extension. We only need to show the existence of C.

Otherwise, $\forall C\in Args$, $\mathcal{E}\left(A\right)+\mathcal{E}\left(C\right)+\rho \left(C\to A\right)<2$, denote

$\underset{C\in Args}{\sup }\left\{\mathcal{E}\left(A\right)+\mathcal{E}\left(C\right)+\rho \left(C\to A\right)\right\}=x$.

Then $x<2$. $Args$ is finite. And $\left(A,\mathcal{E}\left(A\right)+\frac{2-x}{2}\right)\notin \mathcal{E}$ will not be sufficiently attacked by $\mathcal{E}$, because $\forall C\in Args$,

$\left(\mathcal{E}\left(A\right)+\frac{2-x}{2}\right)+\mathcal{E}\left(C\right)+\rho \left(C\to A\right)=x+\frac{2-x}{2}<2.$

Contradiction.

( $\Leftarrow$ ) The first condition confirms $\mathcal{E}$ is conflict-free, while the second equation assures that $\forall A\in Args$, if $a>\mathcal{E}\left(A\right)$, then $\left(A,a\right)$ is sufficiently attacked by $\left(C,\mathcal{E}\left(C\right)\right)$, and thus it is sufficiently attacked by $\mathcal{E}$. Ends.

For the preferred and grounded semantics, their digital properties are very complex. We will show them in future work.

4. Comparison with Other Work

The new semantics is consistent with Dung’s semantics in crisp AFs, which has been proven in [11]. In the next subsections, we will compare the comparative semantics under the Łukasiewicz t-norm (CSL) with some related work, including Wu’s Gödel semantics (WGS) [10] and Janssen’s semantics (JS) [9].

4.1. Comparability to Wu’s Gödel Semantics (WGS)

Definition 6 (Definition 3 in [10] ) In a fuzzy AF $\left(\mathcal{A},\rho \right)$, given two fuzzy arguments $\left(A,a\right)$ and $\left(B,b\right)$, as well as $\rho \left(A\to B\right)$, if

$b\le 1-\min \left\{a,\rho \left(A\to B\right)\right\},$. (1)

then the attack is tolerable, otherwise, it is a sufficient attack.

Definition 7 [Definition 5 and 8 in [10] ]

A fuzzy set of arguments $\mathcal{E}\subseteq \mathcal{A}$ is conflict-free if all attacks between the fuzzy arguments in $\mathcal{E}$ are tolerable.

A conflict-free set of fuzzy arguments $\mathcal{E}\subseteq \mathcal{A}$ is admissible, if $\mathcal{E}$ weakening defends each element in $\mathcal{E}$.

We have the following results：

Theorem 6 In a fuzzy AF $\left(\mathcal{A},\rho \right)$. $\mathcal{E}\subseteq \mathcal{A}$ is conflict-free in WGS, then $\mathcal{E}$ is conflict-free in CSL, but not vice versa.

Proof. By Formula (1), $b+\min \left\{a,\rho \left(A\to B\right)\right\}\le 1$,

$str\left(\left(A,a\right),\left(B,b\right)\right)=\max \left\{0,a+\max \left\{0,{\rho }_{AB}+b-1\right\}-1\right\}=0.$ (2)

Obviously, Formula (1) $\Rightarrow$ Formula (2), but not vice versa.

Example 1 Consider a simple fuzzy AF in the next graph.

Here, $\left\{\left(A,0.7\right),\left(B,0.8\right)\right\}$ is a conflict-free set in CSL, but a conflict set in WGS.

$str\left(\left(A,0.7\right),\left(B,0.8\right)\right)=\max \left\{0,\max \left\{0,0.7+0.4-1\right\}+0.8-1\right\}=0,$

then $\left\{\left(A,0.7\right),\left(B,0.8\right)\right\}$ is conflict-free in CSL. But

$\min \left\{0.7,0.4\right\}+0.8=1.2>1$,

then $\left\{\left(A,0.7\right),\left(B,0.8\right)\right\}$ is conflict in WGS.

The following example shows the two kinds of acceptability are also of difference.

Example 2 In the following graph, $\left(A,0.7\right)$ can defend $\left(C,0.5\right)$ in WGS, but $\left(A,0.7\right)$ can defend $\left(C,0.7\right)$ in CSL.

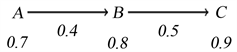
Proof. Since $\min \left\{1-\min \left\{0.7,0.4\right\},0.8,0.5\right\}+0.5=1$, $\left(A,0.7\right)$ weakening defends $\left(C,0.5\right)$ in WGS. And because

$str\left(\left(A,0.7\right),\left(B,0.8\right)\right)=str\left(\left(B,0.8\right),\left(C,0.7\right)\right),$

so $\left(A,0.7\right)$ can defend $\left(C,0.7\right)$ in CSL.

4.2. Comparability to Janssen’s Semantics (JS)

A Janssen’s AF can be defined by associating an element of $\left[\text{0,1}\right]$ with each attack in a Dung’s AF.

Definition 8 [Definition 3 in [9] ] A Janssen’s AF is a tuple $\left(Args,\nrightarrow \right)$, where $Args$ is a crisp set of arguments and $\nrightarrow :Args\times Args\to \left[0,1\right]$ is a fuzzy relation over $Args$.

Definition 9 [Definition 4 in [9] ] Let $\left(Args,\nrightarrow \right)$ be a Janssen’s AF, $x,y\in \left[0,1\right]$.

A fuzzy set $\mathcal{E}$ over $Args$ is x-conflict-free, $\neg \left(\mathcal{E}\nrightarrow \mathcal{E}\right)\ge x$.

A fuzzy set $\mathcal{E}$ over $Args$ is y-admissible, if it defends itself well enough against all attacks, i.e.,

$\underset{B\in Args}{\inf }\left(\left(B\nrightarrow \mathcal{E}\right)⇝\left(\mathcal{E}\nrightarrow B\right)\right)\ge y.$

Theorem 7 (Theorem 5 in [15] )

A fuzzy set $\mathcal{E}$ in $Args$ is X-conflict-free, if $\forall A,B\in Args$, one of $\mathcal{E}\left(A\right)$, $\mathcal{E}\left(B\right)$ or $A\nrightarrow B$ is no more than $1-x$.

Corollary 3 [Corollary 4 in [15] ]

A fuzzy set $\mathcal{E}$ in $Args$ is 1-admissible , if $\forall B,C\in Args$, $\exists A\in Args$, s.t.

$\min \left\{\mathcal{E}\left(C\right),B\nrightarrow C\right\}\le \min \left\{\mathcal{E}\left(A\right),A\nrightarrow B\right\}.$ (3)

Example 3 Consider the example in the next graph.

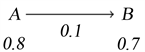
Obviously, $\left\{\left(A,0.8\right),\left(B,0.7\right)\right\}$ is not 1-conflict-free. But

$str\left\{\left(A,0.8\right),\left(B,0.7\right)\right\}=\max \left\{0,0.8+\max \left\{0,0.1+0.7-1\right\}-1\right\}=0,$

$\left\{\left(A,0.8\right),\left(B,0.7\right)\right\}$ is conflict-free.

We have the following conclusions:

Theorem 8 Let $\left(Args,\nrightarrow \right)$ be a fuzzy AF, if $\mathcal{E}$ is 1-conflict-free in JS, then $\mathcal{E}$ is conflict-free in CSL.

Proof. The fuzzy set $\mathcal{E}$ is 1-conflict-free in JS, if $\forall A,B\in Args$,

$\min \left\{\mathcal{E}\left(A\right),\mathcal{E}\left(B\right),A\nrightarrow B\right\}\le 0\iff \mathcal{E}\left(A\right)=0,\mathcal{E}\left(B\right)=0,\text{or}A\nrightarrow B=0,$

in this case, A and B are obviously conflict-free in CSL. But not vice versa, as in Example 3.

Theorem 9 Let $\left(Args,\nrightarrow \right)$ be a fuzzy AF, if $\mathcal{E}$ is 1-conflict-free and 1-admissible in JS, then $\mathcal{E}$ is admissible in CSL.

Proof. According to the definition of our admissibility, $\forall \left(B,\mathcal{A}\left(B\right)\right)$ attacks $\left(C,\mathcal{E}\left(C\right)\right)$, $\exists \left(A,\mathcal{E}\left(A\right)\right)$ attacks $\left(B,\mathcal{A}\left(B\right)\right)$, s.t.

$str\left(\left(A,\mathcal{E}\left(A\right)\right),\left(B,\mathcal{A}\left(B\right)\right)\right)\ge str\left(\left(B,\mathcal{A}\left(B\right)\right),\left(C,\mathcal{E}\left(C\right)\right)\right),$

i.e.,

$\mathcal{E}\left(A\right)+A\nrightarrow B\ge \mathcal{E}\left(C\right)+B\nrightarrow C.$ (4)

Obviously, Formula (3) $\Rightarrow$ Formula (4), but not vice versa.

Wu’s Gödel semantics [10] and Janssen’s semantics [9] can be regarded as special cases of comparative semantics under the Łukasiewicz t-norm.

5. Conclusions

Fuzzy AFs enrich the arguments and/or attacks with fuzzy degrees, capturing the uncertainty issued from the partly trusted information in case of incompleteness, ambiguity, vagueness, etc. This paper is a further study of comparative semantics of fuzzy AFs under the Łukasiewicz t-norm. First, we use the Łukasiewicz t-norm to calculate the str between fuzzy arguments. Then, the numerical properties of the conflict-free sets, the admissible extensions, the complete extensions, and the stable extensions are discussed respectively. Finally, we compare some related works. When it comes to clear arguments and clear attacks, the comparative semantics under the Łukasiewicz t-norm is consistent with Dung’s semantics. Moreover, when fuzzy sets are involved, Wu’s Gödel semantics and Janssen’s semantics can be regarded as special cases of this semantics under the Łukasiewicz t-norm.

The research results of this paper theoretically enrich and develop the comparative semantics of fuzzy AFs. In practical application, various extensions can be quickly and effectively judged. For example, Theorem 1 can quickly check whether a fuzzy argument set is a conflict-free set; Theorem 4 can be used to check whether a fuzzy set is a complete extension or not, and can also be used to calculate complete extensions in fuzzy AFs without sufficient attack cycles.

This paper does not study the algorithms of the grounded extension and the preferred extension, which is our future work. In addition, the results of this paper will greatly reduce the effect of semantic calculation of fuzzy AFs with cycles, which needs to be further improved in the future.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Dung, P.M. (1995) On the Acceptability of Arguments and Its Fundamental Role in Nonmonotonic Reasoning, Logic Programming and N-person Games. Artificial intelligence, 77, 321-357. https://doi.org/10.1016/0004-3702(94)00041-X
[2]	Atkinson, K. and Bench-Capon, T. (2021) Argumentation Schemes in AI and Law. Argument & Computation, 12, 417-434. https://doi.org/10.3233/AAC-200543
[3]	Ferretti, E., Tamargo, L.H., García, A.J., Errecalde, M.L. and Simari, G.R. (2017) An Approach to Decision Making Based on Dynamic Argumentation Systems. Artificial intelligence, 242, 107-131. https://doi.org/10.1016/j.artint.2016.10.004
[4]	Baroni, P., Toni, F. and Verheij, B. (2020) On the Acceptability of Arguments and Its Fundamental Role in Nonmonotonic Reasoning, Logic Programming and N-person Games: 25 Years Later. Argument & Computation, 11, 1-14. https://doi.org/10.3233/AAC-200901
[5]	Cohen, A., Parsons, S., Sklar, E.I. and Mcburney, P. (2018) A Characterization of Types of Support between Structured Arguments and Their Relationship with Support in Abstract Argumentation. International Journal of Approximate Reasoning, 94, 76-104. https://doi.org/10.1016/j.ijar.2017.12.008
[6]	Flouris, G. and Bikakis, A. (2019) A Comprehensive Study of Argumentation Frameworks with Sets of Attacking Arguments. International Journal of Approximate Reasoning, 109, 55-86. https://doi.org/10.1016/j.ijar.2019.03.006
[7]	Baroni, P., Cerutti, F., Giacomin, M. and Guida, G. (2011) AFRA: Argumentation Framework with Recursive Attacks. International Journal of Approximate Reasoning, 52, 19-37. https://doi.org/10.1016/j.ijar.2010.05.004
[8]	Wu, J., Li, L. and Sun, W. (2020) Gödel Semantics of Fuzzy Argumentation Frameworks with Consistency Degrees. AIMS Mathematics, 5, 4045-4064. https://doi.org/10.3934/math.2020260
[9]	Janssen, J., De Cock, M. and Vermeir, D. (2008) Fuzzy Argumentation Frameworks. Proceeding of the 12th Information Processing and Management of Uncertainty in Knowledge-Based Systems, 513-520.
[10]	Wu, J., Li, H., Oren, N. and Norman, T.J. (2016) Gödel Fuzzy Argumentation Frameworks. In: Computational Models of Argument: Proceedings of COMMA 2016, IOS Press, Amsterdam, 447-458.
[11]	Wu, J. (2019) Fuzzy Argumentation Frameworks with Comparing Acceptability. In: Proceeding of the Second Chinese Conference on Logic and Argumentation, Springer, Berlin, 61-73.
[12]	Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. https://doi.org/10.1016/S0019-9958(65)90241-X
[13]	Zhou, X., Wu, Y. and Polochova, V. (2019) Product Conceptual Design Method Based on Intuitionistic Fuzzy Binary Semantics Group Decision Making. Journal of Science and Management, 12, 742-754. https://doi.org/10.4236/jssm.2019.126050
[14]	Sall, M., Kebe, A., Gueye, I. and Diop, M. (2021) Comparative Study between the PID Regulator and the Fuzzy Regulator Applied to the Operation of a Brushless DC Motor. Energy and Power Engineering, 13, 365-376. https://doi.org/10.4236/epe.2021.1311025
[15]	Wu, J. and Oren, N. (2016) Some Properties of Janssen’s Fuzzy Argumentation Frameworks. 1st Chinese Conference on Logic and Argumentation, CLAR 2016, Hangzhou, 2-3 April 2016, 30-37.