Synchronization of Transient Delay-Coupled Network

Yingying Zhang, Yuanguang Zheng

School of Mathematics and Information Science, Nanchang Hangkong University, Nanchang, China.

DOI: 10.4236/jcc.2021.99002                

Abstract

A transient delay-coupled network was proposed by modifying the standard delay-coupled network with a transient coupling technique to enlarge the synchronization domain of the network, where the synchronization domain is the interval of the coupling strength for which the network gets synchronized. The coupling of the transient delay-coupled network is activated when the systems are in a particular region (coupling region) of the phase space and inactivated otherwise, which is different from the standard coupling. The specific synchronization performance of the transient delay-coupled network was investigated through case studies. The relationships between the synchronization domain and the coupling region were obtained by gauging the synchronization index. It is understood that the synchronization domain changes in a non-smooth manner with the variation of the coupling region. In particular, the synchronization domain of a transient delay-coupled network is much larger than that of the standard delay-coupled network when the coupling region is appropriately determined.

Keywords

Delay-Coupled Network, Synchronization, Time Delay, Transient Coupling

1. Introduction

Synchronization is a typical dynamic phenomenon in coupled nonlinear systems [1] . Various synchronization methods have been proposed in the literature, including phase synchronization, complete synchronization, generalized synchronization, and lag synchronization. The strictest type is the complete synchronization, in which all the coupled systems undergo the same dynamical behavior simultaneously. A remarkable finding is that the coupled chaotic systems can achieve complete synchronization [2] . Chaotic synchronization has broad applications in various fields, including secure communications, long-term predictions, and pattern recognition [3] [4] . To study the stability of the synchronized state, a conditional Lyapunov exponent was introduced [5] . The synchronized state is stable if the maximum conditional Lyapunov exponent is negative and thus attains complete synchronization. Network topology plays a crucial role in synchronization. A universal master stability function was suggested to study the effects of the network topology [6] . Based on the master stability function, studies have indicated that fully coupled networks can achieve synchronization with small coupling strengths as long as the network scale is sufficiently large. For a network with the nearest-neighbor structure, synchronization performance decreases consistently as the network scale increases [7] . The synchronization performances of the small-world networks are much better than those of nearest-neighbor networks [8] . The synchronization performances of the scale-free networks increase and saturate when the network scale increases [9] .

Synchronization of networks with time-varying topologies has drawn considerable attention, as researchers have sought to understand the complex collective behaviors of real networks with time-varying structures [10] [11] . There are potential applications for regulating the synchronization of coupled systems by using the switching technique [12] [13] . When the topology of a network switches significantly faster than the dynamic time scale of the coupled nodes, the network behaves as if the coupling is static and equivalent to the case with the time average of the switching connectivity [10] [11] . New collective dynamics can appear if the switching frequency is comparable to the time scale of individual nodes [12] [14] . An intriguing finding is that the switching structure can be beneficial for synchronization of the network [10] [15] . The synchronization domain can be enlarged with on-off coupling, and the synchronization can be attained much faster than that with the static coupling [12] . The synchronization of two coupled Rössler systems is possible when the coupling switches periodically between two values, even if each value of the coupling is not suitable for synchronization [13] .

The transient coupling is one of the simple types of switching structures proposed to enhance the synchronization of driving-driven systems [16] . The coupling is activated only when the system is in a particular region (coupling region) of the state space and is inactivated otherwise. Studies have indicated that the synchronization performance with transient coupling can be better than that with standard coupling when the coupling region is properly chosen [17] . A transient coupling scheme was also used to attain synchronization of a network that was nonsynchronizable with static coupling [18] . The distributions of the eigenvalues of the local Jacobian and the local conditional Lyapunov exponents were also analyzed to understand the effects of transient coupling on the synchronization [17] [19] . It was concluded that transient coupling modifies the collective dynamics of coupled systems in a strongly nonlinear way.

Connection delays are generally incorporated into coupled systems, particularly in large-scale networks and long-distance secure communication networks. Long connection delays result from finite information transmission as well as processing speeds [20] [21] [22] . Networks with connection delays are described by time-delayed systems with infinite-dimensional state spaces. The evolution of time-delayed systems depends on both present and past states. Studies have demonstrated that the synchronization features of delay-coupled systems are substantially different from those of coupled systems without connection delays [20] [23] . For the coupled oscillators without connection delays, amplitude death can occur only when their frequency is disparate. However, amplitude death results from connection delays even if those oscillators have the same frequency [24] . The consequences of connection delays on various cluster states in delay-coupled oscillators with nearest-neighbor structures were studied previously [25] , and it was shown that the mean frequency decreased with the increase of the connection delay. The coupling with connection delays is invasive, and the coupling force still acts on the synchronized system when the synchronization is attained. Thus, the time delay is included in the synchronized system that describes the dynamics of the synchronized state, which will deteriorate the synchronization performance frequently [26] , destabilize the synchronized state [27] , change the dynamics of the synchronized system, and lead to complex synchronous dynamics [23] , resulting in various synchronization transitions [28] .

It is fundamentally necessary to enhance the synchronization performance of delay-coupled networks with applicable methods. To the best of the author’s knowledge, transient delay-coupling has not been introduced into delay-coupled networks, and the effects of the transient delay-coupling on the synchronization of delay-coupled networks have not been investigated. Inspired by this, the transient delay-coupling is introduced into the delay-coupled network to enhance the synchronization performance in this paper, which leads to the transient delay-coupled network. Its specific synchronization features are studied through case studies. The rest of the article is organized as follows: In Section 2, transient delay-coupling is introduced into the delay-coupled network. In Section 3, the specific synchronization performances of the transient delay-coupled network are studied. In the last section, conclusions are drawn from the above investigation.

2. Problem Statement and the Construction of Transient Delay-Coupled Network

A fully coupled network with n identical nodes and a connection delay is described by

${\stackrel{\dot{}}{X}}_i=F\left(X_i\right)+\frac{g}{n-1}\cdot \left(a_{ii}H\left(X_i\right)+{\displaystyle \underset{j=1,j\ne 1}{\overset{n}{\sum }}H\left(X_j\left(t-\tau \right)\right)}\right),i=1,2,\cdots ,n,$ (1)

where ${\stackrel{\dot{}}{X}}_i=F\left(X_i\right)$ describes the dynamics of the ith node, $X_i={\left(x_{i1},x_{i2},\cdots ,x_{im}\right)}^{\text{T}}\in R^m$ is a vector of the state variables, $F(\cdot )={\left(f_1(\cdot ),f_2(\cdot ),\cdots ,f_m(\cdot )\right)}^{\text{T}}\in R^m$ is a vector of nonlinear functions, g is the total coupling strength of each node, $\tau$ represents the connection delay, $H(\cdot )={\left(h_1(\cdot ),h_2(\cdot ),\cdots ,h_m(\cdot )\right)}^{\text{T}}\in R^m$ is the vector of inner coupling functions, and $a_{ij}\left(i,j=1,2,\cdots ,n\right)$ are the coupling coefficients with $$ and $a_{ij}=-{\displaystyle \underset{j=1,j\ne i}{\overset{n}{\sum }}{a}_{ij}}$ .

In the complete synchronization manifold, the dynamics of the synchronized state $X_1=X_2=\cdots =X_n=X$ is determined by

$\stackrel{\dot{}}{X}=F\left(X\right)+g\left(H\left(x-\tau \right)-H\left(x\right)\right)$ . (2)

For a fully coupled network, all the perturbed equations on the transverse directions are the same, described by the master stability function [29] [30]

$\stackrel{\dot{}}{\eta }=DF\eta -g\left(DH\eta +\frac{1}{n-1}D{H}_{\tau }\eta \left(t-\tau \right)\right)$ , (3)

where $\eta$ represents the deviation in the transverse directions of the synchronization manifold, DF is the Jacobian matrix of $F(\cdot )$ , evaluated on the synchronized state $X\left(t\right)$ , and DH and $D{H}_{\tau }$ are the Jacobian matrix of $H(\cdot )$ evaluated at the synchronized state $X\left(t\right)$ and delayed state $X\left(t-\tau \right)$ , respectively. The synchronization manifold is stable, and synchronization is attained when the maximum conditional Lyapunov exponent determined by the master stability function (3) is negative [29] [30] .

The evolution of the master stability function (3) depends on both the present and past states [31] . The initial state is the function ${\eta }_{t_0}\left(\theta \right)=\eta \left(t_0+\theta \right)$ , defined in the Banach space $C=C\left(\left[-\tau ,0\right],R^m\right)$ , where $t_0$ is the initial time, and $\theta \in \left[-\tau ,0\right]$ . The maximum conditional Lyapunov exponent is defined as ${\lambda }_m=\underset{{}_{{\eta }_{t_0}\left(\theta \right)\in C}}{\max }{\lambda }_{{\eta }_{t_0}}\left(\theta \right)$ while

${\lambda }_{{\eta }_{t_0}}\left(\theta \right)=\underset{t\to \infty }{\lim }\frac{1}{t}\cdot \ln \left(\frac{{\Vert {\eta }_{t_0+t}\left(\theta \right)\Vert }_C}{{\Vert {\eta }_{t_0}\left(\theta \right)\Vert }_C}\right)$ , (4)

where ${\Vert \varphi \left(\theta \right)\Vert }_C=\underset{{}_{\theta \in \left[-T,0\right]}}{\max }{\Vert \varphi \left(\theta \right)\Vert }_{L2}$ is the norm of the function $\varphi \left(\theta \right)$ defined in Banach space C, and ${\Vert \cdot \Vert }_{L2}$ denotes the Euclidean norm defined in $R^m$ .

Let $t_i=t_0+ih\left(i=0,1,\cdots ,+\infty \right)$ denote the time series with the step size h, the conditional Lyapunov exponent ${\lambda }_{{\eta }_{t_0}}\left(\theta \right)$ is then described as

$\begin{array}{c}{\lambda }_{{\eta }_{t_0}}\left(\theta \right)=\underset{i\to \infty }{\lim }\frac{1}{ih}\cdot \ln \left(\frac{{\Vert {\eta }_{t_i}\left(\theta \right)\Vert }_C}{{\Vert {\eta }_{t_0}\left(\theta \right)\Vert }_C}\right)=\underset{i\to \infty }{\lim }\frac{1}{ih}\cdot \ln \left({\displaystyle \underset{k=1}{\overset{i}{\prod }}\frac{{\Vert {\eta }_{t_k}\left(\theta \right)\Vert }_C}{{\Vert {\eta }_{t_{k-1}}\left(\theta \right)\Vert }_C}}\right)\\ =\underset{i\to \infty }{\lim }\frac{1}{ih}{\displaystyle \underset{k=1}{\overset{i}{\sum }}\ln \left(\frac{{\Vert {\eta }_{t_k}\left(\theta \right)\Vert }_C}{{\Vert {\eta }_{t_{k-1}}\left(\theta \right)\Vert }_C}\right)}=\underset{i\to \infty }{\lim }\frac{1}{ih}{\displaystyle \underset{k=1}{\overset{i}{\sum }}{l}_k}\end{array}$

$l_k=\ln \left(\frac{{\Vert {\eta }_{t_k}\left(\theta \right)\Vert }_C}{{\Vert {\eta }_{t_{k-1}}\left(\theta \right)\Vert }_C}\right)$ is regarded as the local conditional Lyapunov exponent corresponding to the point $X\left(t_k\right)$ of the synchronized state [32] . $l_k<0$ (or $l_k>0$ ) suggests that the point $X\left(t_k\right)$ is locally stable (or unstable). Thus, the local stability of the point $X\left(t_k\right)$ of the synchronized state depends on its position in the phase space [33] . The conditional Lyapunov exponent ${\lambda }_{{\eta }_{t_0}}\left(\theta \right)$ will decrease when the local conditional Lyapunov exponents $l_k$ diminish overall. Thus, the coupling should be activated when the coupled system is in the region (coupling region) of the phase space where the local conditional Lyapunov exponents are diminished by the coupling and deactivated otherwise, leading to the transient delay-coupled network.

The coupling without a connection delay is not invasive, while the coupling force vanishes when synchronization is attained. However, coupling with a connection delay is invasive, and the coupling force is still acting on the synchronized system when the synchronization is achieved. For delay-coupled systems, the conditions for complete synchronization are strict. One of the conditions is that all the coupled nodes have the same input degree. Thus, the transient coupling scheme proposed for coupled systems without connection delays [16] cannot be applied directly to delay-coupled systems.

In this article, the transient delay-coupling is introduced into the network given by Equation (1) by letting

$a_{ij\left(i\ne j\right)}^s=\{\begin{array}{l}{a}_{ij\left(i\ne j\right)}{X}_i\in \Omega \text{and}{X}_i\in \Omega \\ 0X_i\notin \Omega \text{and}{X}_i\notin \Omega \end{array}$ , (5)

where $\Omega \subseteq R^m$ is the coupling region. Equation (1) becomes

#Math_44# (6)

where, $a_{ii}^s=-{\displaystyle \underset{j=1,j\ne i}{\overset{n}{\sum }}{a}_{ij}^s}$ . The ith node will cut off all the connections with other nodes when $X_i\notin \Omega$ , and all the other coupled nodes still have the same input degree. When $\Omega =R^m$ , the transient delay-coupling in Equation (5) degrades into static delay-coupling with as $a_{ii}^s=a_{ij}$ .

The synchronization performance of the network given by Equation (6) is closely associated with the coupling region $\Omega$ . It is challenging to determine the proper coupling regions analytically such that the network can get synchronization in a large synchronization domain because of the strong nonlinear relationship between the synchronization and the coupling regions [16] [17] . In the present work, the relationship between the synchronization domain of the network, given by Equation (6), and the coupling regions is first obtained by calculating the synchronization index, and the coupling region is determined such that the synchronization is achieved in a large synchronization domain. The effects of the transient delay-coupling were investigated by comparing the synchronization performance of the network given by Equation (6) with transient delay-coupling to that of the network expressed by Equation (1) with static delay-coupling, where the synchronization performance of one network is considered to be better when the synchronization domain is larger [29] [34] .

3. Synchronization of the Transient Delay-Coupled Network

This section examines the specific synchronization features of the transient delay-coupled networks through case studies. To show the advantage of the transient delay-coupling over the standard delay-coupling, we compare the synchronization performance of the transient delay-coupled network and that of the standard delay-coupled network.

Case 1: A fully delay-coupled network with nodes of the Hindmarsh-Rose (HR) neuron coupled via the x component only is considered, as follows:

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_i=y_i-a{x}_i^3+b{x}_i^2-z_i+I+\frac{g}{n-1}\cdot {\displaystyle \underset{j=1,j\ne i}{\overset{n}{\sum }}{a}_{ij}^s\left(x_j\left(t-\tau \right)-x_i\right)}\\ {\stackrel{\dot{}}{y}}_i=c-d{x}_i^2-y_i\\ {\stackrel{\dot{}}{z}}_i=r\left[s\left(x_i+x_0\right)-z_i\right]\end{array}$ (7)

where $x_i$ , $y_i$ and $z_i$ are the state variables of the ith node, representing the membrane potential, exchange of ions across the neuron membrane, and a slowly changing adaptation current, respectively; I is the membrane input current for biological neurons, r is usually a small parameter related to the slow variable $z_i$ , and $x_0$ represents the resting potential of the system [35] .

The HR system is the minimal model that can reproduce several electrical firing activities observed in real biological neuron activities. HR neuron networks have been studied intensively to understand the collective dynamics of real neural networks [30] [36] . In the following analysis, the system parameters were fixed to be $a=1$ , $b=3$ , $c=1$ , $d=5$ , $s=4$ , $x_0=-1.6$ , $r=0.004$ and $I=3.25$ such that the single neuron produces bursting oscillations.

The collective dynamics are evaluated by the synchronization index defined as

$S_{dex}={\left(n-1\right)}^{-1}{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}\langle {\Vert X_{i+1}\left(t\right)-X_i\left(t\right)\Vert }_{L2}\rangle }$ . (8)

where, $X_i\left(t\right)={\left(x_i\left(t\right),y_i\left(t\right),z_i\left(t\right)\right)}^{\text{T}}$ is the vector of state variables of ith node, $\langle \cdot \rangle$ represents the average over a sufficiently long time after the transient process. Smaller synchronization index $S_{dex}$ corresponds to better collective dynamics, and $S_{dex}=0$ indicates complete synchronization.

As the synchronization performance of the transient delay-coupled network (7) is closely related to the coupling region $\Omega$ , a proper coupling region $\Omega$ should first be established. There are different ways to change the coupling signal with different types of coupling regions. For the sake of simplifying the study, consider one of the simplest types of coupling regions:

${\Omega }_{S_l}=\left\{\left(x,y,z\right)|x\le S_l\right\}$ . (9)

As shown in Figure 1, the coupling region ${\Omega }_{S_l}$ is determined by the switching line $S_l$ . The control signal is only activated when $x\le S_l$ . Since the switching line $S_l$ is only related to the available variable x, it is convenient to realize the transient delay-coupling by detecting the available variable x online.

Figure 1. The bursting oscillation of HR neuron projected on $\left(x,z\right)$ -plane, and the coupling region ${\Omega }_{S_l}$ (gray region), determined by the switching line $S_l$ .

Without loss of generality, the synchronization performances of the network provided by Equation (7) with network scale $n=10$ and different connection delays $\tau$ were studied for $g\in \left[0,1.5\right]$ . The synchronization domain is the interval of the coupling strength g for which the network gets synchronized. The relationships between the synchronization domain and the coupling region ( $S_l$ ) are obtained in Figure 2, which shows the synchronization domain changes in a non-smooth manner with the variation of the controlling region.

To demonstrate the advantage of the transient delay-coupling over the standard delay-coupling, comparisons between the control performance of the transient delay-coupled network with a proper controlling region ${\Omega }_{S_l}$ and that of the standard delay-coupled network are given in Figure 3. It is shown the synchronization domain of the transient delay-coupled network is much larger than that of the standard delay-coupled network when the controlling region is appropriately determined. This result is confirmed by the time series in Figure 4.

Case 2: The transient delay-coupled Rössler systems connected linearly via the x component only is considered, as follows:

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_i=-\left(y_i+z_i\right)+\frac{g}{n-1}\cdot {\displaystyle \underset{j=1,j\ne i}{\overset{n}{\sum }}{a}_{ij}^s\left(x_j\left(t-\tau \right)-x_i\right)}\\ {\stackrel{\dot{}}{y}}_i=x_i+a{y}_i\\ {\stackrel{\dot{}}{z}}_i=b+z_i\left(x_i-c\right)\end{array}$ (10)

The dynamics of coupled Rössler systems have been studied intensively to understand the collective phenomena of coupled chaotic systems [5] [13] . Here, the transient delay-coupling is introduced into the network, and the impacts of the transient delay-coupling on the synchronization performance are examined. In the subsequent analysis, the system parameters are fixed at $a=\text{0}\text{.2}$ , $b=\text{0}\text{.2}$ , and $c=\text{5}\text{.7}$ , for which the single Rössler system exhibits chaotic dynamics.

The collective dynamics of the transient delay-coupled network given by Equation (10) are again evaluated by the synchronization index defined in Equation (8), and the simplest type of coupling region ${\Omega }_{S_l}$ described in Equation (9) is used to construct the transient delay-coupling in the network. The synchronization performances of the network with network scale $n=10$ and different

Figure 2. The relationships between the synchronization domain of network 7) and the switching line $S_l$ , where the value of the synchronization index $S_{dex}$ is indicated by the color, with a saturation value of 0.005, and the synchronization domain is the interval of g where $S_{dex}=0$ . Left: Network scale $n=10$ and connection delay $\tau =0.2$ . Right: Network scale $n=10$ and connection delay $\tau =1$ .

Figure 3. Comparisons between the synchronization performance of the transient delay-coupled network and that of the standard delay-coupled network, the blue solid lines, and red dash lines indicate the synchronization indexes corresponding to transient delay-coupling and standard delay-coupling, respectively. Left: The transient delay-coupled network with a controlling region ${\Omega }_{S_l}$ ( $S_l=0.3$ ). Right: The transient delay-coupled network with a controlling region ${\Omega }_{S_l}$ ( $S_l=0.4$ ).

Figure 4. Collective dynamics of network (7) with scale $n=10$ and different system parameters. Left: Asynchronization with standard delay-coupling ( $\Omega =R^m$ ). Right: Synchronization with transient delay-coupling ( $\Omega ={\Omega }_{S_l}$ ).

connection delays $\tau$ are examined for $g\in \left[0,10\right]$ . The relationships between the synchronization domain and the controlling region are obtained in Figure 5, which indicates the synchronization domain varies in a non-smooth manner with the variation of the controlling region.

To instantiate the advantage of the transient delay-coupling over the standard delay-coupling, comparisons between the control performance of the transient delay-coupled network with a proper controlling region ${\Omega }_{S_l}$ and that of the standard delay-coupled network are given in Figure 6. It is shown the synchronization domain of the transient delay-coupled network is larger than that of the standard delay-coupled network when the controlling region is appropriately determined. This outcome is confirmed by the time series in Figure 7.

Summarizing the conclusions obtained from the above case studies, the synchronization performance of the transient delay-coupled network is closely related to the coupling region. The synchronization domain changes in a non-smooth fashion with the variation of the controlling region. In particular, the transient delay-coupling proposed in this paper is beneficial to the synchronization performance of the delay-coupled network; the synchronization domain of the transient delay-coupled network is much larger than that of the standard delay-coupled network when the coupling region is appropriately determined.

Figure 5. The relationships between the synchronization domain of network (10) and the switching line $S_l$ , where the value of the synchronization index $S_{dex}$ is indicated by a color, with a saturation value of 0.005, and the synchronization domain is the interval of g where $S_{dex}=0$ . Left: Network scale $n=10$ and connection delay $\tau =0.1$ . Right: Network scale $n=10$ and connection delay $\tau =0.5$ .

Figure 6. Comparisons between the synchronization performance of the transient delay-coupled network and that of the standard delay-coupled network, the blue solid lines, and red dash lines indicate the synchronization indexes corresponding to transient delay-coupling and standard delay-coupling, respectively. Left: The transient delay-coupled network with a controlling region ${\Omega }_{S_l}$ ( $S_l=3.6$ ). Right: The transient delay-coupled network with a controlling region 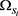( $S_l=-2.6$ ).

Figure 7. Collective dynamics of network (10) with scale $n=10$ and different system parameters. Left: Asynchronization with standard delay-coupling ( $\Omega =R^m$ ). Right: Synchronization with transient delay-coupling ( $\Omega ={\Omega }_{S_l}$ ).

4. Conclusion

Delay-coupling is invasive as the delay-coupling force still acts on the synchronized system when the synchronization is achieved. The connection delay destabilized the synchronization manifold frequently and deteriorated the synchronization performance of the delay-coupled network. It is of fundamental importance to improve the synchronization performance of the delay-coupled network. The transient delay-coupled network was proposed, for the first time, by applying the transient coupling technique to the standard delay-coupled network. Case studies have indicated that the synchronization performance of the delay-coupled network is much better than that of the standard delay-coupled network when the coupling region is appropriately chosen. From the practical application point of view in engineering, the transient delay-coupled network has some advantages over the standard delay-coupled network. For example, in some real networks, the coupling strength is restricted to a particular limited domain of the parameter space. In this case, the synchronization domain of the transient delay-coupled network can be changed and enlarged to make the coupling strength fall within the synchronization domain by choosing an appropriate coupling region, and thus, the synchronization is attained. Different than the continuous coupling force of the standard delay-coupled network, the coupling force of the transient delay-coupled network is only activated in the coupling region. Consequently, the transient delay-coupled network is low-cost and conserves energy, especially when the coupling region is small. Besides, the results obtained in the present paper can help to understand the synchronization of real delay-coupled networks with time-varying structures.

Acknowledgements

This paper was supported by the NSF of China under Grants 11872197, 12072140, and the JXNSF of China under Grant 20192BAB202002.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Pikovsky, A., Rosenblum, M. and Kurths, J. (2001) Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge University Press, New York. https://doi.org/10.1017/CBO9780511755743
[2]	Pecora, L.M. and Carroll, T.L. (1990) Synchronization in Chaotic Systems. Physical Review Letters, 64, 821-824. https://doi.org/10.1103/PhysRevLett.64.821
[3]	Landsman, A.S. and Schwartz, I.B. (2007) Complete Chaotic Synchronization in Mutually Coupled Time-Delay Systems. Physical Review E, 75, Article ID: 026201. https://doi.org/10.1103/PhysRevE.75.026201
[4]	Samir, B. and Salem, A. (2019) The Fractional Chua Chaotic System: Dynamics, Synchronization, and Application to Secure Communications. International Journal of Nonlinear Sciences and Numerical Simulation, 20, 1-12. https://doi.org/10.1515/ijnsns-2018-0195
[5]	Pecora, L.M., Carroll, T.L., Johnson, G.A. and Mar, D.J. (1997) Fundamentals of Synchronization in Chaotic Systems, Concepts, and Applications. Chaos, 7, 520-543. https://doi.org/10.1063/1.166278
[6]	Pecora, L.M. and Carroll, T.L. (1998) Master Stability Functions for Synchronized Coupled System. Physical Review Letters, 80, 2109-2112. https://doi.org/10.1103/PhysRevLett.80.2109
[7]	Chen, G.R., Wang, X.F. and Li, X. (2012) Introduction to Complex Networks: Models, Structures and Dynamics. Higher Education Press, Beijing.
[8]	Barahona, M. and Pecora, L.M. (2002) Synchronization in Small-World Systems. Physical Review Letters, 89, Article ID: 054101. https://doi.org/10.1103/PhysRevLett.89.054101
[9]	Wang, X.F. and Chen, G. (2002) Synchronization in Scale-Free Dynamical Networks: Robustness and Fragility. IEEE Transactions on Circuits and Systems, 49, 54-62. https://doi.org/10.1109/81.974874
[10]	Belykh, I.V., Belykh, V.N. and Hasler, M. (2004) Blinking Model and Synchronization in Small-World Networks with a Time-Varying Coupling. Physica D, 195, 188-206. https://doi.org/10.1016/j.physd.2004.03.013
[11]	So, P., Cotton, B.C. and Barreto, E. (2008) Synchronization in Interacting Populations of Heterogeneous Oscillators with Time-Varying Coupling. Chaos, 18, Article ID: 037114. https://doi.org/10.1063/1.2979693
[12]	Chen, L., Qiu, C. and Huang, H.B. (2009) Synchronization with On-Off Coupling: Role of Time Scales in Network Dynamics. Physical Review E, 79, 045101(R). https://doi.org/10.1103/PhysRevE.79.045101
[13]	Buscarino, A., Frasca, M., Branciforte, M., Fortuna, L. and Sprott, J.C. (2017) Synchronization of Two Rossler Systems with Switching Coupling. Nonlinear Dynamics, 88, 673-683. https://doi.org/10.1007/s11071-016-3269-0
[14]	Kohar, V., Ji, P., Choudhary, A., Sinha, S. and Kurths, J. (2014) Synchronization in Time-Varying Networks. Physical Review E, 90, Article ID: 022812. https://doi.org/10.1103/PhysRevE.90.022812
[15]	Li, S., Sun, N., Chen, L. and Wang, X. (2018) Network Synchronization with Periodic Coupling. Physical Review E, 98, Article ID: 012304. https://doi.org/10.1103/PhysRevE.98.012304
[16]	Schroder, M., Mannattil, M., Dutta, D., Chakraborty, S. and Timme, M. (2015) Transient Uncoupling Induces Synchronization. Physical Review Letters, 115, Article ID: 054101. https://doi.org/10.1103/PhysRevLett.115.054101
[17]	Ghosh, A., Godara, P. and Chakraborty, S. (2018) Understanding Transient Uncoupling Induced Synchronization through Modified Dynamic Coupling. Chaos, 28, Article ID: 053112. https://doi.org/10.1063/1.5016148
[18]	Schroder, M., Chakraborty, S., Witthaut, D., Nagler, J. and Timme, M. (2016) Interaction Control to Synchronize Nonsynchronizable Networks. Scientific Reports, 6, Article No. 37142. https://doi.org/10.1038/srep37142
[19]	Tandon, A., Schroder, M., Mannattil, M., Timme, M. and Chakraborty, S. (2016) Synchronizing Noisy Nonidentical Oscillators by Transient Uncoupling. Chaos, 26, Article ID: 094817. https://doi.org/10.1063/1.4959141
[20]	Wang, Q.Y., Perc, M., Duan, Z.S. and Chen, G.R. (2009) Synchronization Transitions on Scale-Free Neuronal Networks Due to Finite Information Transmission Delays. Physical Review E, 80, Article ID: 026206. https://doi.org/10.1103/PhysRevE.80.026206
[21]	Rifhat, R., Muhammadhaji, A. and Teng, Z. (2018) Global Mittag-Leffler Synchronization for Impulsive Fractional-Order Neural Networks with Delays. International Journal of Nonlinear Sciences and Numerical Simulation, 19, 205-213. https://doi.org/10.1515/ijnsns-2017-0179
[22]	Petkoski, S. and Jirsa, V.K. (2019) Transmission Time Delays Organize the Brain Network Synchronization. Philosophical Transactions of the Royal Society A, 377, Article ID: 20180132. https://doi.org/10.1098/rsta.2018.0132
[23]	Zheng, Y. and Wang, Z. (2012) Time-Delay Effect on the Bursting of the Synchronized State of Coupled Hindmarsh-Rose Neurons. Chaos, 22, Article ID: 043127. https://doi.org/10.1063/1.4768664
[24]	Reddy, K.V.R., Sen, A. and Johnston, G.L. (1998) Time Delay Induced Death in Coupled Limit Cycle Oscillators. Physical Review Letters, 80, 5109-5112. https://doi.org/10.1103/PhysRevLett.80.5109
[25]	Nakamura, Y., Tominaga, F. and Munakata, T. (1994) Clustering Behavior of Time-Delayed Nearest-Neighbor Coupled Oscillators. Physical Review E, 49, 4849-4856. https://doi.org/10.1103/PhysRevE.49.4849
[26]	Hsia, C.-H., Jung, C.-Y., Kwon, B. and Ueda, Y. (2020) Synchronization of Kuramoto Oscillators with Time-Delayed Interactions and Phase Lag Effect. Journal of Differential Equations, 268, 7897-7939. https://doi.org/10.1016/j.jde.2019.11.090
[27]	Bottcher, P.C., Otto, A., Kettemann, S. and Agert, C. (2020) Time Delay Effects in the Control of Synchronous Electricity Grids. Chaos, 30, Article ID: 013122. https://doi.org/10.1063/1.5122738
[28]	Tang, J., Ma, J., Yi, M., Xia, H. and Yang, X.Q. (2011) Delay and Diversity-Induced Synchronization Transitions in a Small-World Neuronal Network. Physical Review E, 83, Article ID: 046207. https://doi.org/10.1103/PhysRevE.83.046207
[29]	Dhamala, M., Jirsa, V.K. and Ding, M. (2004) Enhancement of Neural Synchrony by Time Delay. Physical Review Letters, 92, Article ID: 074104. https://doi.org/10.1103/PhysRevLett.92.074104
[30]	Zheng, Y. and Wang, Z. (2016) Network-Scale Effect on Synchronizability of Fully Coupled Network with Connection Delay. Chaos, 26, Article ID: 043103. https://doi.org/10.1063/1.4946812
[31]	Hale, J.K. and Lunel, S.M.V. (1993) Introduction to Functional Differential Equations. Springer-Verlag, New York. https://doi.org/10.1007/978-1-4612-4342-7
[32]	Wolf, R.C.L. (1992) Local Lyapunov Exponents: Looking Closely at Chaos. Journal of the Royal Statistical Society: Series B, 54, 353-371. https://doi.org/10.1111/j.2517-6161.1992.tb01886.x
[33]	Eckhardt, B. and Yao, D. (1993) Local Lyapunov Exponents in Chaotic Systems. Physica D, 65, 100-108. https://doi.org/10.1016/0167-2789(93)90007-N
[34]	Zheng, Y. and Bao, L. (2017) Effect of Topological Structure on Synchronizability of Network with Connection Delay. Chaos, Solitons & Fractals, 98, 145-151. https://doi.org/10.1016/j.chaos.2017.03.035
[35]	Hindmarsh, J.L. and Rose, R.M. (1984) A Model of Neuronal Bursting Using Three Coupled First-Order Differential Equations. Proceedings of the Royal Society of London. Series B, 221, 87-102. https://doi.org/10.1098/rspb.1984.0024
[36]	Wang, Q.Y., Zheng, Y.H. and Ma, J. (2013) Cooperative Dynamics in Neuronal Networks. Chaos, Solitons & Fractals, 56, 19-27. https://doi.org/10.1016/j.chaos.2013.05.003