Development of a Numerical Scheme

R. B. Ogunrinde, T. E. Olaosebikan

Department of Mathematical Sciences, Ekiti State University, Ado Ekiti, Nigeria.

DOI: 10.4236/ajcm.2016.61006                

Abstract

In this paper, we developed a new numerical scheme which aimed to solve some initial value problems of ordinary differential equations. The full breakdown of this new numerical scheme derivation is presented. While in our subsequent research, we shall fully examine the characteristics of the scheme such as consistency, convergence and stability. Also, the implementation of this new numerical scheme shall be worked-on and comparison shall also be made with some existing methods.

Keywords

Numerical Scheme, Ordinary Differential Equation, Scheme Development

Received 19 February 2016; accepted 27 March 2016; published 30 March 2016

1. Introduction

Many numerical analysts such as: S. O. Fatunla [1] , E. A. Ibijola [2] [3] , R. B. Ogunrinde [4] and even A. A. Obayomi [5] and so on, have developed schemes for the solution of some initial value problem of ordinary differential equations. The efficiency of all these contributed effort from this numerical analyst in numerical analysis had been measured and tested for their stability, accuracy, convergence and consistency properties. The accuracy properties of different methods are usually compared by considering the order of convergence as well as the truncation error coefficients of the various methods (C. F. Tischer, 1984). From literatures, this shows that so many methods which are suitable for solving some sets of initial value problems (ivps) in ordinary differential equations (ODEs) must have all the mentioned characteristics.

Ogunrinde, R. B. [4] , developed a scheme in which standard finite difference schemes were developed. Similarly, Obayomi, A. A. [5] [6] , also worked on some approximation techniques which was used to derive qualitatively stable non-standard finite difference schemes.

In this paper, a new numerical scheme was developed with the above mentioned characteristics in mind to solve some initial value problems of ordinary differential equations which was based on the local representation of the theoretical solution to initial value problem of the form:

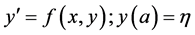in the interval 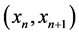by interpolating function 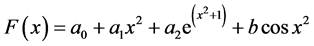, where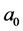, , 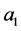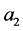and b are real undetermined coefficients.

2. Derivation of the New Scheme

Suppose we have the initial value problem:

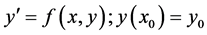(1)

Let us assume that the theoretical solution to (1) can be locally represented in the interval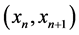, 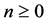by the interpolating polynomial function:

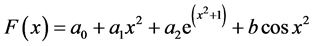(2)

where, , 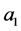, 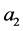and b are real undetermined coefficients.

We shall assume that 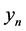is a numerical estimate to the theoretical solution and. We define mesh points as follows:

Therefore, from (2), we proceed to the scheme derivation as follows:

(3)

(4)

(5)

(6)

from (2),

(7)

from (3),

(8)

from (4),

(9)

from (5),

(10)

putting (8) into (9), we have:

multiply through by, we have:

(11)

putting (11) into (10), we obtain:

(12)

putting (12) into (11), we obtained:

(13)

putting (12) and (13) into (8), we have:

Now,

(14)

Let

Therefore,

(14a)

Now, imposing the following constraints on the interpolating function (2) in the following order:

1) The interpolating function (2) must coincide with the theoretical solution at and such that:

2) The derivative of and coincide with and respectively. i.e.

from conditions (1) and (2) above, it follows that:

if, then, we have:

Collecting like-terms

So,

(15)

Now, suppose:

(16)

Also,

(17)

from (15), we have:

(18)

Similarly,

by factorization, we have:

(19)

(20)

Putting (16) through (20) into (15), we have the new scheme follows:

(21)

Equation (21) is the proposed scheme.

3. Conclusions

We aim to develop a new numerical scheme which can favourably agree with the existing ones for solving some initial value problems of ordinary differential equations. Clearly, this paper has been able to show the development of the new numerical scheme as proposed.

In our subsequent research, we shall pay more attention on the implementation of this new scheme to solve some initial value problems (ivp) of the form (1) and also compare the results with the existing methods and thereafter we examine the characteristics properties such as the stability, convergence, accuracy and consistency of the scheme.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Fatunla, S.O. (1987) An Implicit Two-Point Numerical Integration Formula for Linear and Non-Linear Stiff System of ODEs. Mathematics of Computation, 32, 1-11. http://dx.doi.org/10.1090/S0025-5718-1978-0474830-0
[2]	Ibijola, E.A. (1997) A New Numerical Scheme for the Solution of Initial Value Problem (IVPs). Ph.D. Thesis, University of Benin, Nigeria.
[3]	Ibijola, E.A. (1998) On the Convergence, Consistency and Stability of a One-Step Method for Integration of ODEs. International Journal of Computer Mathematics, 73, 261-277.
[4]	Ogunrinde, R.B. (2010) A New Numerical Scheme for the Solution of Initial Value Problems in Ordinary Differential Equations. Ph.D. Thesis, University of Ado Ekiti, Nigeria.
[5]	Obayomi, A.A. (2012) Derivation of Non-Standard Finite Difference Schemes for the Second Order Chemical Reaction Model. Canadian Journal on Computing in Mathematics, Natural Sciences, Engineering and Medicine, 3, 121-124.
[6]	Obayomi, A.A. (2012) A Set of Non-Standard Finite Difference Schemes for the Solution of an Equation of the Type International Journal of Pure and Applied Sciences and Technology, 12, 34-42.